球面小波背景误差协方差模型的设计

曹小群，张卫民，宋君强，刘柏年

国防科学技术大学计算机学院，长沙 410073

球面小波背景误差协方差模型的设计

曹小群，张卫民，宋君强，刘柏年

国防科学技术大学计算机学院，长沙 410073

在全球变分资料同化系统中设计和实现了基于球面小波的背景误差协方差（B）模型。引入框架理论构造了球面小波函数；设计了一个基于球面小波变换的全球B矩阵模型；分别通过理想数值试验和在全球变分同化系统中的实现对新模型的有效性进行了验证。试验结果表明：基于球面小波的背景误差协方差模拟方法能够克服由有限背景误差样本引入的取样噪声，能估计出真实的背景误差相关函数；在全球变分同化系统中新模型能够模拟出在物理和动力上正确和有效的背景误差结构函数。

背景误差协方差；球面小波；变分资料同化；数值天气预报

1 引言

以高性能计算为基础的数值天气预报（NWP）技术能有效克服一般预报方法产品不够丰富、可用预报时效短、海量气象观测数据处理能力弱等缺点，已经成为气象部门制作业务天气预报的根本科学途径。全球大气资料同化是把全球范围观测资料和对大气运动的动力学认识进行最优结合的一类信息融合方法，目的是产生出与所有已知信息（包括观测资料、背景场及它们对应的误差信息）最一致的大气状态场。大规模并行计算机性能的不断发展有力地推动着全球中期数值天气预报模式分辨率的不断提高，当前条件下发展业务化的全球中小尺度数值天气预报系统已成为可能，从而使全球中期数值天气预报系统能为台风和暴雨等灾害性天气的预报和监测提供更好的科学依据[1]。全球数值天气预报模式分辨率的提高对提供初始场的资料同化[2-9]系统也提出了新要求：资料同化系统分辨率需要相应提高，同时背景误差协方差模型必须能刻画不同尺度（包括行星尺度、大尺度、中尺度和中小尺度等）大气运动的误差统计特征[9]。

在目前业务化的全球变分同化系统中，一般都采用谱空间对角化方法来模拟背景误差协方差[9-10]，谱空间对角方法对所有大气运动尺度的背景误差不加分别地统一处理，其计算结果反映的是各种尺度的平均统计误差特征。在这种情况下，小尺度或小振幅的大气波动的背景误差特征完全有可能被大尺度或大振幅的运动特征所掩盖。谱空间对角化方法的另一个缺点是将相同的相关函数应用在所有的物理位置，不能够描述实际垂直相关或水平相关随空间的变化[9-10]；第二种模拟全球B矩阵的方法是物理空间格点方法：分别用经验正交函数（EOF）和递归滤波模拟垂直相关和水平相关函数，然后把它们应用到全球模式格点空间上[11-12]。物理格点方法能表示B-矩阵在物理空间的信息，但会把同样的相关应用到所有运动尺度上。综上所述，如果只使用谱方法，就不能刻画背景协方差在物理空间的变化特征；如果在格点空间表示B，就不能刻画协方差随波动尺度变化的特征。总之，单独用谱方法或者格点空间方法都不能刻画B的所有特征。

小波函数在谱和格点空间中同时具有局部性，能够将相关函数同时表示为尺度和位置两者的函数。正交小波函数具有光滑性、紧支撑、滤波和正交性等许多良好的性质，其适合解决定义域为矩形区域的问题[13-15]，曹小群等采用正交小波模拟了区域变分资料同化系统中的水平误差相关函数[16]。但将正交小波分析扩展到球面区域是困难的：因为在球面上构建正交小波一般都存在“极点问题”[17]，所以构造球面小波需要采用引入新的数学工具。本文根据Fisher等[8-9]的思想，研究利用框架理论[17-18]构造能够应用于业务化的全球气象变分同化系统的球面小波函数，设计了全球变分资料同化中基于球面小波函数的B矩阵模型。

2 球面小波函数构造

如果给出一个被一组有限正交小波基表示的函数，对此函数在球面上作任意旋转后，则新函数不能被同样的小波基表示[17]。因此构造球面小波函数只能考虑非正交变换，适合的数学工具之一是框架。对于Hilbert空间Η中的一个函数族{φn;n∈Γ}，其中Γ是离散指标的可数集，如果存在常数0＜A≤B＜+∞使得下面不等式

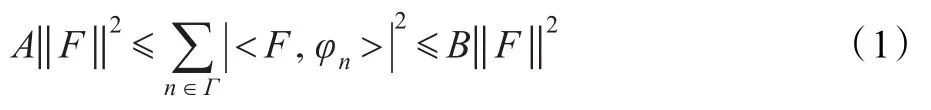
对任意函数F∈H成立，则此函数族构成一个离散框架[17]。在式（1）中如果常数A=B，则称此函数族为紧框架[17]。如果指标集Γ在某一个测度μ下是可测的，同时满足下面的条件：

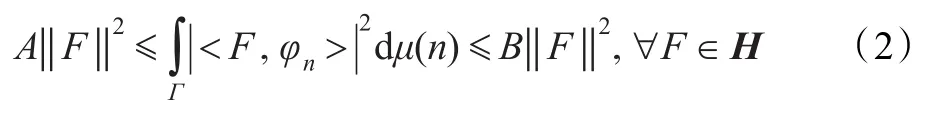
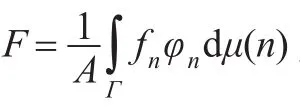
上面的叙述表明在框架的意义下，非正交函数族能够精确地表示信号，能对函数进行分解和重构。利用球面上的紧框架条件可构造具体的球面小波函数。选择一个波数节点序列{Nj;j∈Z}，且N0=0和Nj＜Nj+1。定义基函数Wj的谱系数为：

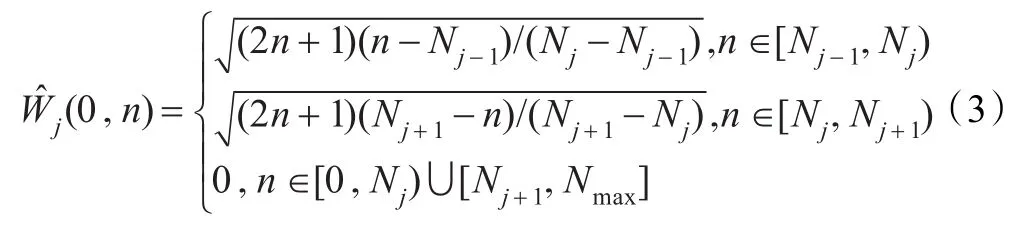
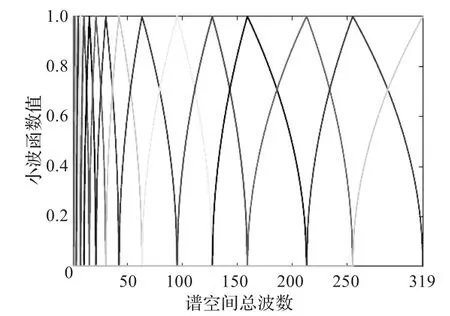
图1 不同球面小波函数在谱空间的取值

同时，在上面描述的紧框架解释中，可以认为fj在一个特定点(λ，φ)的值代表了小波基函数W(λ，φ，j)的系数。为了使这个解释有意义，要求函数W(λ，φ，j)在点(λ，φ)周围是局部化的。在图2～3中分别显示了第11个和第15个球面小波函数在谱空间和物理空间中值的分布图。谱空间中的小波函数是总波数的函数，只在有限区间中非零，而在区间以外为零。物理空间中的小波函数是大圆距离（这里用角度表示）的函数，从图中可以看出，函数呈现了很好的局部性。图4显示的是第10个和第11个球面小波函数在二维球面格点空间上的分布图，从图中可知，球面小波函数只在局部区域非零，呈现了很好的局部性。因此，每个球面小波函数的系数场只由球面上的有限格点上的值正确决定，例如，对于高斯网格，将由2Nj+1个经度格点和(2Nj+1+1)/2个纬度格点上值决定。

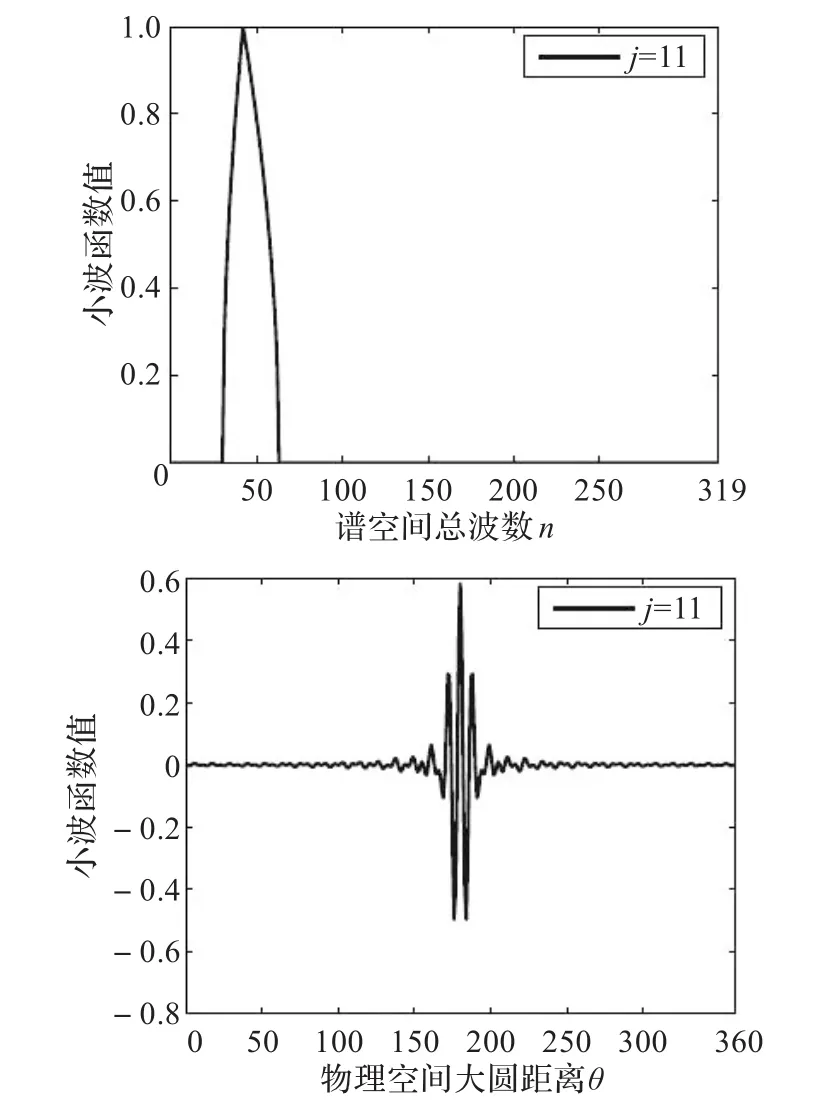
图2 第11个球面小波函数在谱空间和物理空间中值的分布图

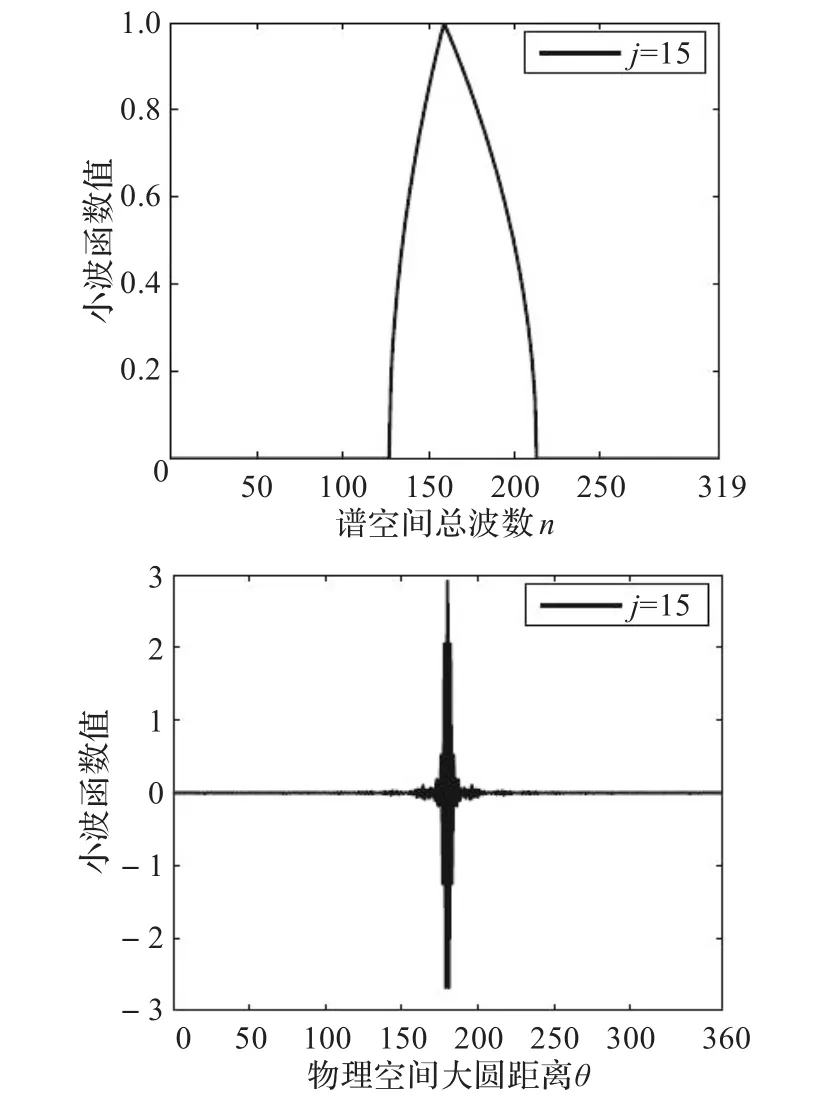
图3 第15个球面小波函数在谱空间和物理空间中值的分布图

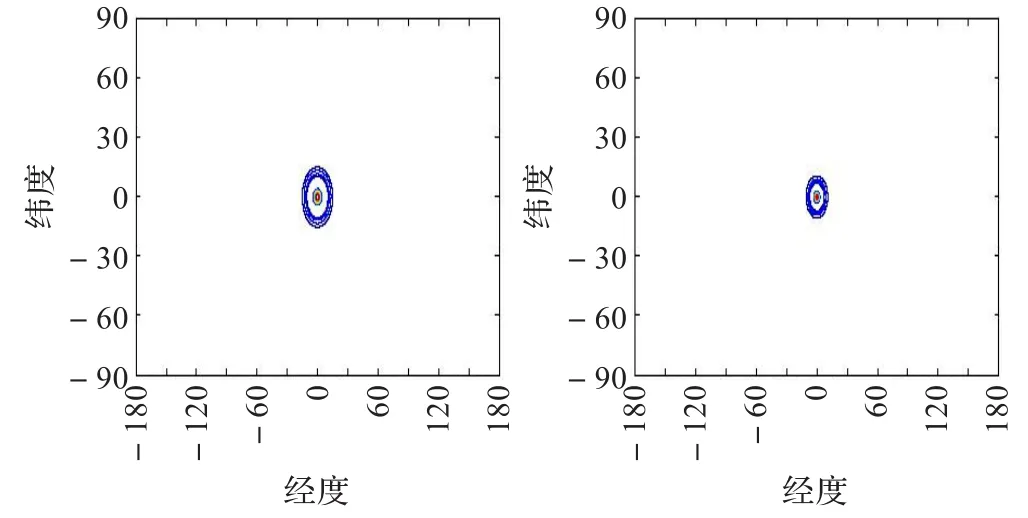
图4 第10和11个球面小波函数在二维球面格点空间中的等值线分布图

获得球面小波函数后，球面上的任何一个函数或者全球大气物理场F（例如，温度、压强、水平风场和湿度等）都可以通过小波函数族Wj进行分解和重构。F和每一个小波函数的卷积⊗将得到小波系数函数fj。由于总数波和空间尺度之间存在对应关系，因此每一个小波系数函数fj都可以被认为代表了一个特定的空间尺度。与球面小波函数卷积的结果使物理场中不同空间尺度的部分被分离，因为小波函数同时在物理空间和谱空间上是局部化的，从而在对应的系数fj所描述的特征中保留了它们的局部性质。每个函数fj和对应小波函数Wj的卷积之和能实现对函数或物理场F的重建。

3 基于球面小波的全球B矩阵模型

利用上面部分定义的球面小波函数Wj可以构造一个背景误差协方差B的模型。因为球面小波函数同时在谱空间和物理空间中具有局部化特性，因此基于Wj的背景误差协方差模型能提供同时在格点空间和尺度上变化的背景误差特征量。又因为球面小波函数具有多尺度分析的能力，因此基于球面小波函数的B矩阵模型能刻画不同尺度大气运动的背景误差特征。

全球变分资料同化是通过极小化目标泛函来估计大气真实状态的离散向量x[20-23]。

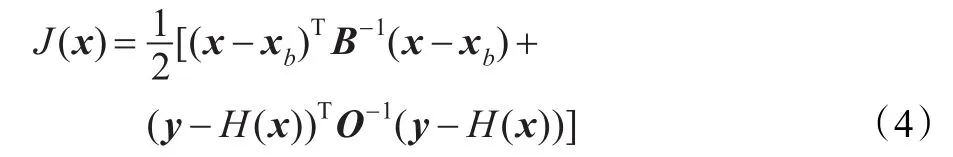
其中xb是对x的先验（背景场）估计，y是观测向量，H是把模式状态量映射到观测空间的算子。矩阵O和B分别是观测和背景误差协方差矩阵。

一般地，对方程（4）中定义的目标泛函直接进行最小化，在数值计算上是坏条件的[21-22]。因此通常的做法是定义一个控制向量v，利用它对背景误差协方差矩阵进行对角化。通过一个控制向量转换可以确定分析增量δx：

在控制变量v空间中，目标泛函可以写成：

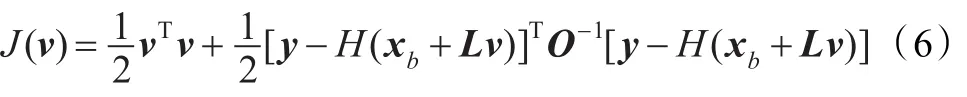
在方程（6）中B矩阵无需显式表示，而是通过控制变换L被隐式地表示。可以很容易地证明，假如B=LLT，则极小化J(v)和J(x)将得到相同的大气状态估计量。因此在全球变分同化中背景误差协方差矩阵不需要直接定义，实际应用中是将其定义为一系列控制变换，即通过选择一个合适的控制变量v和变换矩阵L来实现的，对于变换矩阵L，无需假设为可逆的，甚至不要求是方阵[9]。

为了定义一个基于小波变换的B矩阵模型，定义控制向量vT=(，，…，，…，)，j=1，2，…，K标识不同尺度的小波空间。其中：

其中K表示不同气象变量之间的物理变换矩阵，包含了平衡约束关系。Vj(λ，φ)表示在j尺度小波空间水平位置(λ，φ)上的垂直协方差矩阵，V(λ，φ)表示它的逆均方根矩阵。原则上，对每一个Wj⊗K-1δx，都必须在格点空间上指定一个垂直协方差矩阵。而在实际计算中，有必要减少垂直协方差矩阵的数目，方法是许多相邻的格点使用同一个垂直协方差矩阵。

在目标泛函的极小化过程中不需要使用式（7），而只需要使用控制向量到分析增量的转换关系式。从上面所定义的新控制向量和方程式（7），可以导出新的基于球面小波的控制变量转换关系式：

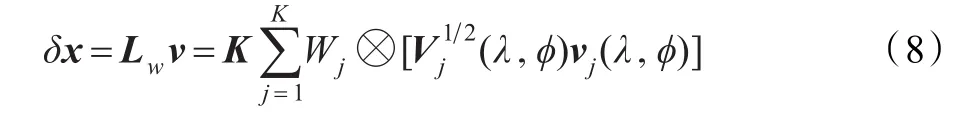
通过上面的分析容易知道，基于球面小波的B矩阵模型所需要的背景误差统计量如下：

（1）物理变换K中需要用到的统计回归系数：速度势和流函数之间的回归系数；温度和流函数之间的回归系数；地面气压和流函数之间的回归系数。

（2）每个控制向量在每个尺度和每个水平位置上的局地垂直相关矩阵Vj(λ，φ)，由于这部分统计参数需要巨大的资料存储量，因此只能在相对变分同化系统更低分辨率的格点上进行垂直统计量的计算。在分析过程中，将低分辨率的统计量插值到同化系统的格点上。

和一般B矩阵模拟方法（例如，著名的WRF变分同化系统）相比，本文设计球面小波B矩阵模型具有以下不同。首先，普通模拟方法中控制变量转换包含的子变换按照作用顺序依次为：物理变换、垂直变换和水平变换；而基于球面小波的控制变量转换包含的子变换按照作用顺序为：物理变换、水平变换和垂直变换。后者的水平变换按照作用顺序又分为：对格点场进行球谐变换；在谱空间中进行球面小波变换；小波变换后，进行逆球谐变换，将谱数据转换成格点场。因此，球谐变换、球面小波变换和逆球谐变换三部分一起构成球面小波控制变量转换中的水平变换。其次，需要的统计量不同，普通模拟方法中需要回归系数、垂直特征值和特征向量以及水平功率谱等统计量。而球面小波控制变量转换中需要统计量是：平衡回归系数、同时依赖于小波尺度和水平位置的局地垂直相关协方差的均方根矩阵及其转置矩阵。

4 数值试验与分析

4.1 理想试验

为了验证球面小波全球B矩阵模型的有效性，首先将进行理想数值试验：使用上面构造的球面小波函数模拟大圆上的协方差函数，从而说明球面小波的滤波性质。研究的地理区域是半径为a的地球大圆。坐标x表示距离，变化范围是[0，2πa]。试验中只考虑大圆上一个物理场，例如一维温度场。假设圆周上有均匀分布的121个格点xj，j=0，1，…，120，同时使用具有变化特征长度尺度的高斯函数来指定格点上真实的背景误差相关函数Ct。特征长度尺度l(x)在个格点1和121上具有最大值：6.5倍格点距；在格点61上具有最小值：1.5倍格点距，其他格点上的特征长度尺度在最大值和最小值之间是线性变化的。Ct表示如下：

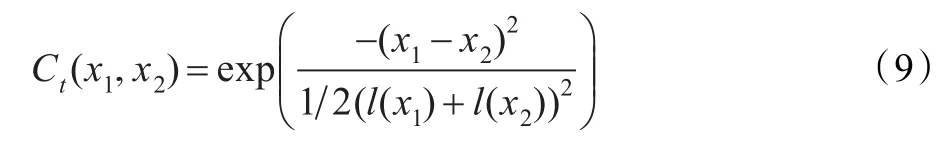
在已知Ct的情况下，可以通过随机模拟方法产生背景误差样本，公式如下：

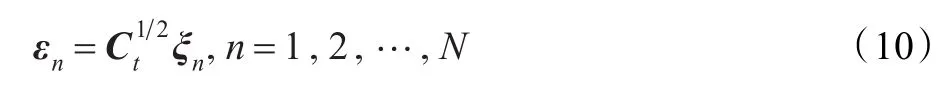
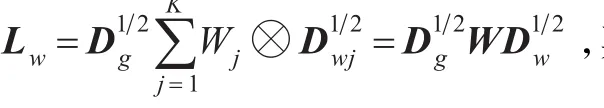
（1）对随机模拟的误差样本{εn，n=1，2，…，50}进行统计，得到格点标准偏差D，然后对误差样本进行规则化=Dεn，n=1，2，…，50。

获得统计量后可以计算出隐含的协方差矩阵，用公式表示为：

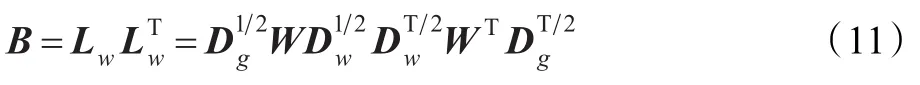
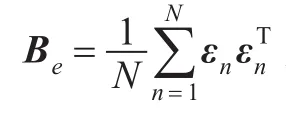
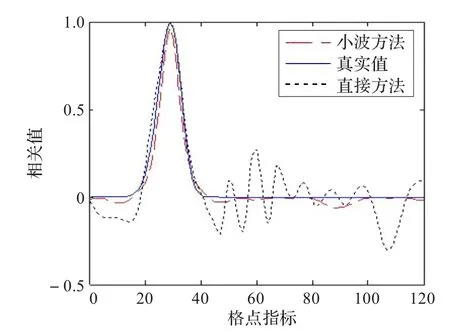
图5 第30个格点上的相关函数比较

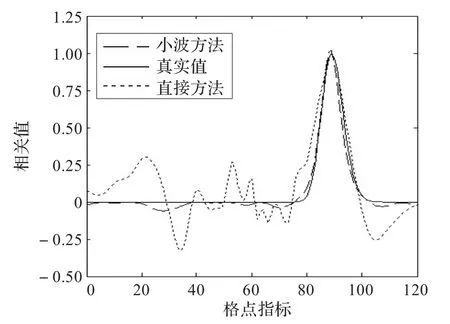
图6 第90个格点上的相关函数比较

总之，通过上面的数值试验说明了基于球面小波的背景误差协方差模拟方法能够克服由有限样本数引入的取样噪声，表明了球面小波形式的背景误差协方差在模拟真实误差相关函数的有效性。虽然这里只对地球大圆上的一维问题进行了试验，但结论同样适应于球面上的二维和三维情形。

4.2 新模型在全球变分同化系统中的实现

为了检验球面小波背景误差协方差矩阵模型的正确性，利用已经实现的全球四维变分资料同化系统（YH4DVAR）[22]进行了单个观测资料同化试验。首先将新的B矩阵模型实现到YH4DVAR中，同时采用NMC方法[23-25]估计了全球背景误差统计量，在此基础上利用最优化算法对目标泛函进行极小化求解。

在资料同化系统中，由单点观测生成的分析增量隐含地表现了背景场误差协方差矩阵B的作用，因此Thepaut等在1991年[20]引入了单点试验方法来反映变分同化中B矩阵的结构函数。在变分资料同化系统中，如果假设观测为单个模式变量，就有：

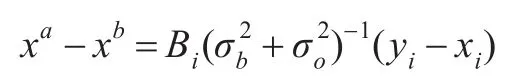
其中的yi是第i个网格点上的单个观测，xi是从背景场计算得到的相关等价量，σo和σb分别是观测和背景场误差，Bi是背景场误差协方差的第i列。从上式可以明显看出，分析增量xa-xb是正比于背景场误差协方差。单点观测的信息传播依赖于背景场误差协方差矩阵，B矩阵在变分同化系统的信息传播中起着重要作用。

图7显示的是YH4DVAR系统在采用新的背景误差协方差模型后对北半球中纬度单个温度观测（经纬度为（122.78°W，53.90°N），高度为800 Hpa）进行同化后，产生的地面气压（图7（a）），模式第7层上的温度（图7（b））、纬向风（图7（c））、经向风（图7（d））和风矢量（图7（e））的水平分析增量。单点观测试验通过全球变分同化系统YH4DVAR可以产生全球范围的增量，但在距离观测较远格点上的增量为零，即单个观测资料对分析场的影响在空间上局部化的，因此上面所有的图只显示靠近观测点区域上的增量。各个分析增量的分布在物理是一致的，具体解释如下：在观测位置上温度的升高，引起气压降低，从而形成辐合风场，但由于受地转科氏力的作用，形成在观测位置以左为北风，观测位置以右为南风的增量分布；低层的辐合将产生上升气流，在高层引起气体质量堆积，从而形成辐散风场，但受地转科氏力的作用，形成观测位置以左为南风，观测位置以右为北风的增量分布，子图图7（e）显示在模式第7层位于观测气压层797.0 Hpa以上，从而形成了一个反气旋式的风场。分析结果表明新的背景误差协方差模型在物理和动力上是正确和有效的。

图7中的另外一个显著特点是纬向风和经向风的增量形状和地转协方差中的增量分布比较相似，但明显具有各向异性特征，即相关结构函数的值随两点的刚性平移或旋转而变化。这主要是因为基于球面小波的背景误差协方差矩阵能够模拟局地的、多尺度大气运动的相关特征。从图7中可以明显看到，球面小波背景误差协方差具有模拟细微相关特征的能力，而基于谱方法的背景误差协方差模型只能均匀和各向同性地向观测位置周围传播信息。从而表明，新模型能够正确地刻画YH4DVAR中实际背景误差协方差矩阵的物理结构函数。

5 结束语

超高分辨率的全球数值天气预报模式将具有多尺度模拟和预报能力，预报产生中将包含行星尺度、大尺度和中小尺度等天气系统的运动信息。为了提供适合该类数值天气预报模式的初始场，有必要在变分资料同化系统中构造能对不同尺度大气波动的背景误差特征分别进行刻画的B矩阵模型。本文利用球面小波方法设计了一个新的全球B矩阵模型，首先引入框架理论构造了球面小波函数；其次构造了一个基于球面小波变换的全球B-矩阵模型；最后分别通过理想数值试验和在全球变分同化系统YH4DVAR中的实现对新B矩阵模型的有效性进行了验证。主要结论是：基于球面小波的背景误差协方差模拟方法能够克服由有限背景误差样本引入的取样噪声，能估计出真实的背景误差相关函数；在全球变分同化系统中新B矩阵模型能够模拟出在物理和动力上是正确和有效的背景误差结构函数。

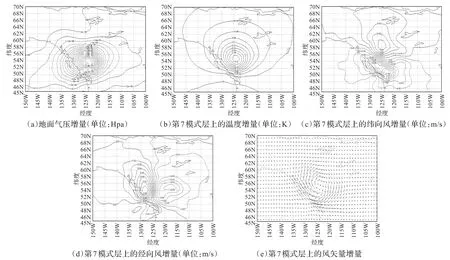
图7 采用新模型后，对于单个温度观测资料，YH 4DVAR所产生的分析增量分布图

[1]Bader D A.Petascale computing：algorithms and applications[M].New York：Chapman & Hall，2007.

[2]Zou X，Navon I M，Le Dimet F X.An optimal nudging data assimilation scheme using parameter estimation[J].Q J R Meteor Soc，1992，118：1163-1193.

[3]Navon I M.Practical and theoretical aspects for adjoint parameter estimation and identifiability in meteorology and oceanography[J].Dyn Atmos Oceans，1997，27：55-79.

[4]黄思训，韩威，伍荣生.结合反问题技巧对一维海温模式变分资料同化的理论分析及数值试验[J].中国科学，2003，47：903-911.

[5]Talagrand O，Courtier P.Variational assimilation of meteorological observations with the adjoint and vorticity equation.Part I：theory[J].Q J R Meteorol Soc，1987，113：1311-1328.

[6]黄思训，蔡其发，项杰，等.台风风场分解[J].物理学报，2007，56（5）：3022-3027.

[7]钟剑，费建芳，黄思训，等.模式误差弱约束四维变分同化研究[J].物理学报，2012，61（14）.

[8]Fisher M，Andersson E.Developments in 4D-Var and Kalman filtering[J].ECMWF Tech Memo，2001，347：38-65.

[9]Fisher M.Background error covariance modelling[C]//Proc of ECMWF Seminar on Recent Developments in Data Assimilation for Atmosphere and Ocean，2004：45-64.

[10]Derber J，Bouttier F.A reformulation of the background error covariance in the ECMWF global data assimilation system[J].Tellus，1999，51A：195-221.

[11]Purser R，Wu W S，Parrish D，et al.Numerical aspects of the application of recursive filters to variational statistical analysis.Part I：spatially homogeneous and isotropic Gaussian covariances[J].M on Wea Rev，2003，131：1524-1535.

[12]Purser R，Wu W S，Parrish D，et al.Numerical aspects of the application of recursive filters to variational statistical analysis.Part II：spatially inhomogeneous and anisotropic general covariances[J].Mon Wea Rev，2003，131：1536-1548.

[13]Jawerth B，Sweldens W.An overview of wavelet based multiresolution analyses[J].SIAM Rev，1994，36（3）：377-412.

[14]Fournier A.Introduction to orthonormal wavelet analysis with shift invariance：application to observed atmospheric blocking spatial structure[J].J Atmos Sci，2000，57：3856-3880.

[15]Deckmyn A，Berre L.Wavelet approach to representing backgrond error covariances in a limited area model[J].Mon Wea Rev，2004，133：1279-1294.

[16]曹小群，黄思训，杜华栋.变分同化中水平误差函数的正交小波模拟新方法[J].物理学报，2008，57（3）：1984-1989.

[17]Kaiser G A.Friendly guide to wavelets[M].Boston：Birkhauser，1994.

[18]Daubechies I.Ten lectures on wavelets，CBMS-NSF series on applied mathematics[M].Philadelphia，PA：SIAM，1992.

[19]Bannister R N.Can wavelets improve the representation of forecast error covariances in variational data assimilation?[J] Mon Wea Rev，2007，135：387-408.

[20]Thepaut J N，Courtier P.Four-dimensional data assimilation using the adjoint of a multi-level primitive equation model[J].Quart J Roy Meteor Soc，1991，117：1225-1254.

[21]Courtier P，Andersson E，Heckley W，et al.The ECMWF implementation of three dimensional variational assimilation（3D-Var）.Part I：formulation[J].Quart J Roy Meteor Soc，1998，124：1783-1808.

[22]张卫民，曹小群，宋君强.以全球谱模式为约束的四维变分资料同化系统YH4DVAR的设计和实现[J].物理学报，2012，61（24）.

[23]Parrish D F，Derber J C.The national meteorological center’s spectral statistical-interpolation analysis system[J].Mon Wea Rev，1992，120：1747-1763.

[24]Berre L.Estimation of synoptic and mesoscale forecast error covariances in a limited area model[J].Mon Wea Rev，2000，128：644-667.

[25]Fisher M，Courtier P.Estimating the covariance matrices of analysis and forecast error in variational data assimilation[J].ECMWF Tech Memo，1995，220：1-28.

CAO Xiaoqun, ZHANG Weimin, SONG Junqiang, LIU Bainian

School of Computer Science, National University of Defense Technology, Changsha 410073, China

Based on spherical wavelet, a new model of background error covariance（B）in global variational data assimilation system is designed and implemented. The frame theory is introduced, which is used to construct the basis functions of spherical wavelet. A model of B-matrix is designed based on spherical wavelet transform. The validity of the new method to model global B-matrix with spherical wavelet is demonstrated by numerical and simple experiments. The results of experiments show that the method has the ability to filter the sample noise from limited number of background error member effectively and to estimate the background error correlation functions correctly.

background error covariance; spherical wavelet; variational data assimilation; numerical weather prediction

CAO Xiaoqun, ZHANG Weimin, SONG Junqiang, et al. Design of background error covariance’s model with spherical wavelet. Computer Engineering and Applications, 2014, 50（17）：49-55.

A

TN911.72

10.3778/j.issn.1002-8331.1308-0296

国家自然科学基金（No.41105063）；高分青年创新基金（No.GFZX 04060103-5-19）。

曹小群（1980—），男，博士，副研究员，研究领域为计算机应用技术、数值天气预报技术、反问题；张卫民（1966—），男，博士，研究员，研究领域为计算机应用技术、数值天气预报技术；宋君强（1962—），男，院士，研究员，研究领域为数值天气预报技术、高性能计算；刘柏年（1985—），男，助理研究员，研究领域为计算机应用技术、数值天气预报技术。E-mail：caoxiaoqun@nudt.edu.cn

2013-08-22

2013-11-15

1002-8331（2014）17-0049-07

CNKI网络优先出版：2014-01-26,http://www.cnki.net/kcms/doi/10.3778/j.issn.1002-8331.1308-0296.htm l