随机特征上一致中心调节的支持向量机

廖士中，卢玮

天津大学计算机科学与技术学院，天津 300072

随机特征上一致中心调节的支持向量机

廖士中，卢玮

天津大学计算机科学与技术学院，天津 300072

支持向量机（SVM）是最为流行的分类工具，但处理大规模的数据集时，需要大量的内存资源和训练时间，通常在大集群并行环境下才能实现。提出一种新的并行SVM算法，RF-CCASVM，可在有限计算资源上求解大规模SVM。通过随机傅里叶映射，应用低维显示特征映射一致近似高斯核对应的无限维隐式特征映射，从而用线性SVM一致近似高斯核SVM。提出一致中心调节的并行化方法。具体地，将数据集划分成若干子数据集，多个进程并行地在各自的子数据集上独立训练SVM。当各个子数据集上的最优超平面即将求出时，用由各个子集上获得的一致中心解取代当前解，继续在各子集上训练直到一致中心解在各个子集上达到最优。标准数据集的对比实验验证了RF-CCASVM的正确性和有效性。

并行支持向量机；大规模数据集；有限资源；随机傅里叶特征；一致中心调节

1 引言

支持向量机（SVM）[1]是在统计学习理论基础上发展起来的一类重要的学习方法，是目前最为流行的数据挖掘方法。

SVM的本质是求解一个二次凸优化问题。当样本数据规模l较大时，训练SVM的空间复杂性为O(l2)，时间复杂性为O(l3)。在传统PC机上已经无法求解大规模SVM学习问题，因而基于计算机集群、超级计算机并行环境下的并行SVM方法应运而生。

现有并行SVM可分为两类。一类是对已有的串行SVM算法进行并行化。包括对SMO算法的并行化实现[2-3]，对内点法的并行化实现[4]以及对梯度下降算法的并行化[5]。对已有的流行SVM串行算法进行并行化，虽然能缓解串行算法对内存的极大需求以及极长的训练时间，但同时也增加了大量通信和同步开销。另一类是设计新的算法，使其算法框架易于并行。Collobert等提出在各个子集上并行训练出多个SVM，再通过神经网络求出最终的SVM[6]。Graf等提出级联SVM的思想[7]。在树状结构中，将下层SVM的支持向量组合作为新的支持向量训练SVM。这两种并行方法减少了训练过程中频繁的数据通信。进程间的通信仅发生在各个SVM之间，但是这些方法需要训练多个SVM。Hazan等提出一种适于分布式并行的SVM算法[8]。使用一个全局校正量对各个子集上迭代求出的解进行校正，使其接近全局解。Forero等采用ADMM框架获得全局校正量[9]。基于全局校正思想的并行SVM在整个算法中只需求解一次SVM。在解优化问题的过程中，每轮迭代之后，各个进程间进行通信，获得全局校正量。

这些并行SVM方法都依赖于大型的计算平台，通过扩大集群规模，增加计算资源来缓解计算复杂性，并未从根本上解决处理大规模问题面临的瓶颈。本文提出资源有限的大规模SVM求解的并行方法。首先，应用随机傅里叶特征[10-12]一致近似核函数。核矩阵的计算是训练核SVM的主要开销。随机傅里叶映射能根据核函数确定出显示特征映射，从而将只能核化处理的非线性问题转化为映射后特征空间上的线性问题。这一方法可根据现有资源来确定随机采样规模，避免求解并存储核矩阵，从而合理地降低了计算复杂性和对计算资源的需求。然后，提出一致中心调节的策略来设计高效的并行算法，进一步缩短训练时间。基于全局校正的并行SVM思想[9]，但考虑到在求解优化算法的早期，每次优化求出的临时解具有很强的随机性，此时进行校正没有意义，因而在每个子集上解优化问题的迭代早期，不进行全局校正。只有当子数据集上的临时解趋于最优解时，才应用一致中心量对子集上的迭代解进行校正，各个进程间才进行通信。该并行化设计相比在全过程中采用一致量进行校正的方法，减少了数据通信量，降低了进程间的通信开销。在各个子集上求解优化问题可采用通用的SVM求解器。通过傅里叶特征映射将核SVM转化为线性SVM，再应用并行一致中心调节的策略训练线性SVM，可使过去只能在超级计算机或计算集群上处理的任务，也能在计算资源有限的环境下快速地训练并保持原有的预测能力。在标准数据集上进行对比实验充分表明，该算法在大规模的数据集上取得非常好的实验结果。

2 随机傅里叶特征

首先介绍机傅里叶特征的相关知识。随机傅里叶特征的概念是由Rahim i等[10]首先提出的。其理论基础来源于调和分析中的博赫纳定理。

定理1（博赫纳定理[13]）Rd上的连续函数F(x)是正定的当且仅当F(x)为某一有限非负Borel测度μ的傅里叶变换，F(x)=∫Rde-ix'tdμ(t)。

对任一正定平移不变核函数k(x，y)=κ(x-y)，都有k(x，y)=∫Rdp(γ)e-iγ'(x-y)dγ，其中，p(γ)为γ的概率密度函数。

令ζγ(x)=e-iγ'x，则k(x，y)=E[ζγ(x)ζγ(y)*]，*表示共轭。ζγ(x)ζγ(y)*为k(x，y)的无偏估计。当k(x，y)和 p(γ)均为实数时，用ψγ(x)=[cos(γ'x+2πθ)]代替ζγ(x)， γ服从密度函数为p(γ)的分布，θ服从[0，1]分布。为减小样本方差，采用蒙特卡罗方法随机采样得到E[ζγ(x)ζγ(y)*]。对γ和θ采样D次，构造映射Ψ:x→则有k(x，y)≈Ψγ(x)'Ψγ(y)。

对于有界的随机变量，存在Hoffeding不等式：

定理2（Hoffeding不等式）设相互独立的随机变量ξ1，ξ2，…，ξN，满足ξi∈[a，b]，i=1，2，…，N，记=1/则对任意ε＞0，有：

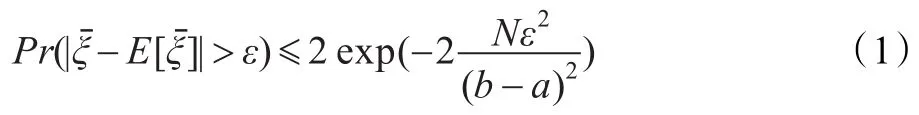
按照上述构造傅里叶特征的方法，结合定理2得到以下定理。

定理3[10]在一给定的数据集S={(x1，y1)，(x2，y2)，…，(xl，yl)}，有：

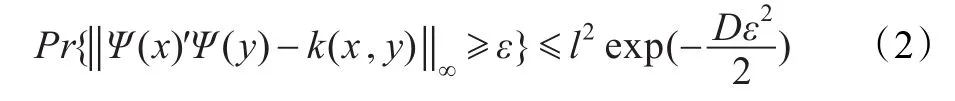
该定理保证了在给定数据集上，用随机特征近似核函数的误差界。

3 一致中心调节框架

给定训练数据集S={(x1，y1)，(x2，y2)，…，(xl，yl)}，xi∈Rd为输入向量，yi=±1对应两类输出。SVM求解优化问题：

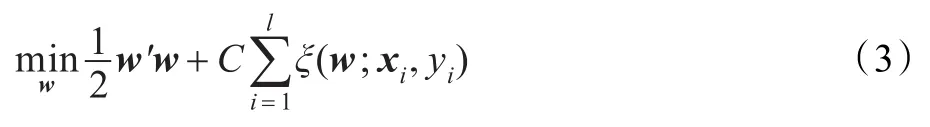
其中，ξ(w;xi，yi)为损失函数，C＞0为惩罚项系数。对于L1-SVM，ξ(w;xi，yi)=max(1-yiw'φ(xi)，0)；对于L2-SVM，ξ(w;xi，yi)=max(1-yiw'φ(xi)，0)2。将训练实例{1，2，…，l}划分为m块{B1，B2，…，Bm}，式（3）可写为：

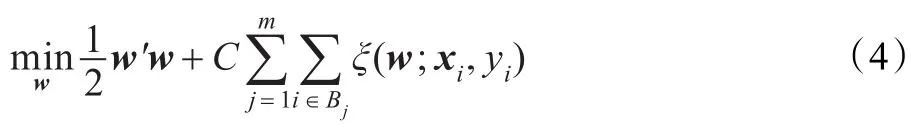
将式（4）分解成m个子问题，在每个子数据块上求解以下问题：

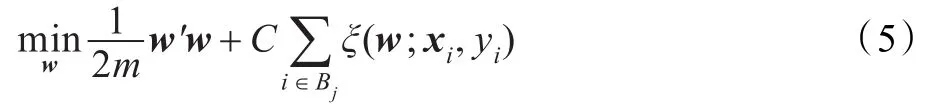
在各个子数据块上训练得到的w不能保证一致。通过对各个子数据块上的w进行校正，让各个子数据块上的w最终收敛到相同的值，获得在整个数据集上的解w。对各个子数据块上训练过程中的得到的w按照如下方法进行校正：各个处理器并行的在子数据集上采用标准SVM求解器求解w，在求解原优化问题或对偶优化问题的过程中生成序列{wk}或{αk}。当各个处理器上分别求出的wk或αk均满足松弛的最优性条件时，主处理器收集各个处理器上得到的w或α，并将其平均值作为对各个子数据集上训练出的w或α进行校正，发送给各个子数据集上，作为下一轮迭代的输入，各进程在子数据集上继续求优化解。重复以上过程，直到所有进程上的优化问题求解完毕。此时，各个进程上的w均收敛到相同的值。

并行算法框架设计如下：将数据集分割成m块，分别存储到m个进程中。m个进程并行的的在子数据上训练SVM。子进程算法的基本流程图如图1所示。

图1 并行框架流程图

该并行过程相比于其他的并行SVM算法，极大地减少了数据通信和同步操作。在训练过程的早期，各个进程间不需要通信。直到在各个子进程上求出的解接近最优解时，进程间才开始通信。

4 并行算法：RF-CCASVM

本章给出基于傅里叶特征应用一致中心调节的详细算法RF-CCASVM，并对算法进行理论分析。

4.1 算法描述

最常使用的核函数为高斯核，因此给出构造高斯核的傅里叶特征的详细算法。训练线性SVM使用简单高效的对偶坐标下降算法[14]。给出在一致中心调节框架下的对偶坐标下降算法。

4.1.1 高斯核的随机傅里叶特征

对于高斯核k(x，y)=exp(-‖x-y‖2/2σ2)，根据傅里叶逆变换求得对应的分布函数为N(0，Id/σ2)。求高斯核的随机傅里叶特征的算法描述如下：

4.1.2 并行框架下的对偶坐标下降

对偶坐标下降算法求解SVM的对偶问题。问题（3）的对偶问题为：

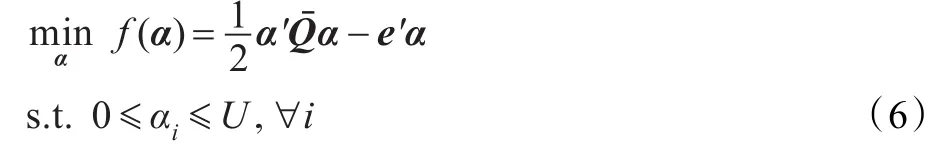
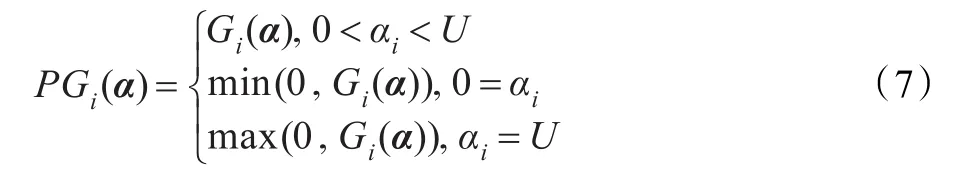
当PGi(α)=0，α在第i维上的值已是最优，不需要更新。否则按以下规则更新αi：

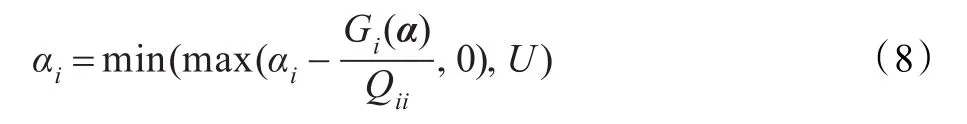
并行一致调节SVM算法将经傅里叶映射后的数据均匀的划分到各个进程上，根据并行框架，使用该对偶坐标下降算法求解。具体的算法描述如下：

4.2 算法分析

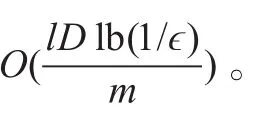
度量并行算法性能的两个常用指标为：加速比和并行效率。

理想情况下，加速比应为m，并行效率达到1。但由于并行算法中存在通信开销，加速比＜m，并行效率＜1。

5 实验与分析

实验在配置为2.3 GHz（双核）CPU，4 GB内存的PC机上完成。MPI并行环境使用MPICH。首先在数据集Web，IJCNN和CovType上进行实验，比较RF-CCASVM与LIBSVM的运行性能。CovType为多分类数据集，仅考虑将第2类其他类相区分的2分类问题。CovType数据集没有测试数据。将CovType数据集的9/10作为训练集，余下的1/10作为测试集。数据集信息见表1。

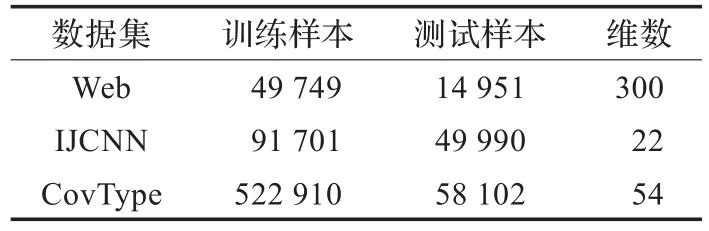
表1 实验用标准数据集

LIBSVM采用高斯核。两个算法的最优参数(C，g)均通过5折交叉验证得到。使用选出的最优(C，g)训练SVM。算法的参数设置见表2。NA表示LIBSVM在CovType数据集上无法运行。

表2 算法参数设置

首先比较RF-CCASVM与LIBSVM的运行时间。实验结果如图2所示。RF-CCASVM算法极大地缩短了在数据集上的训练时间。数据集越大，该算法的高效性越明显。在CovType数据集上，LIBSVM在PC机上无法实验，在有限的内存上，RF-CCASVM仍可快速地进行训练。

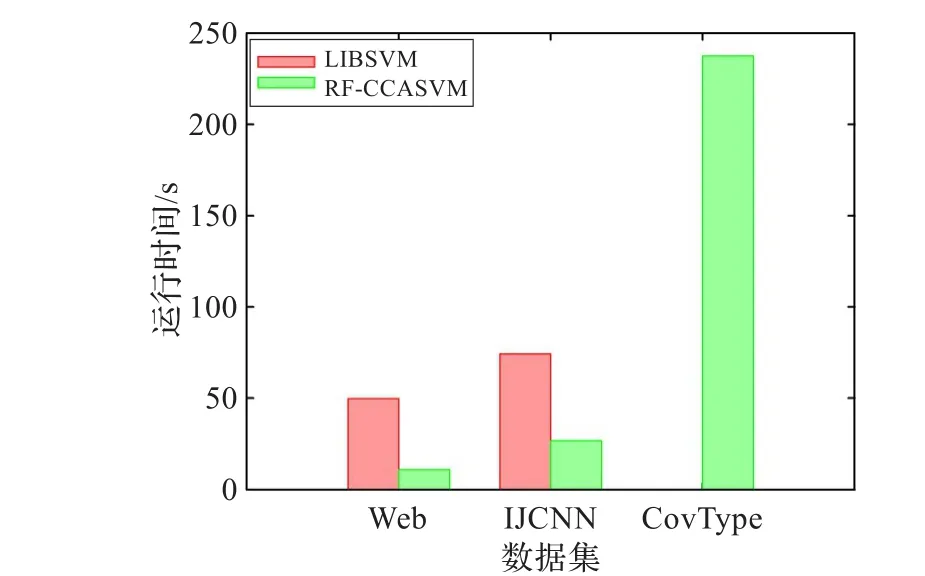
图2 RF-CCASVM与LIBSVM运行时间比较

接下来比较RF-CCASVM与LIBSVM在标准数据集上的预测精度。实验结果如图3所示。RF-CCASVM为近似算法，有一致近似界的保证。算法的预测结果非常接近LIBSVM的精确解。尽管该算法是近似求解，但仍有非常高的预测准确率。

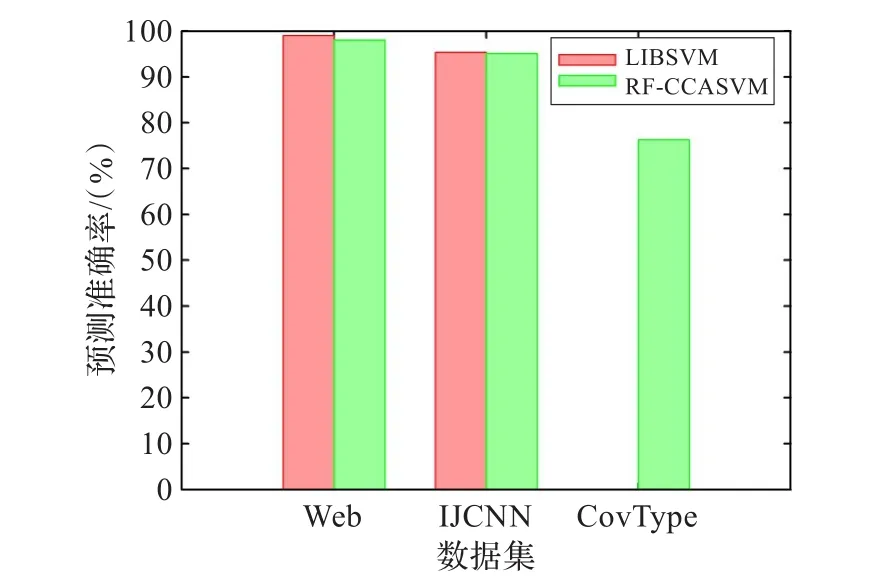
图3 RF-CCASVM与LIBSVM预测准确率比较

另外还进行RF-CCASVM算法的可扩展性实验。使用不同的进程数进行实验，统计训练时间，计算加速比。实验结果如图4所示。线性训练过程非常快，因而通信和同步代价对并行算法的执行时间有较大影响。在该并行算法中，进程间通信D维向量。因此，高维的傅里叶特征会增加通信开销。该算法在数据集上较小时会有一定的不稳定性。在较小的数据集上，加速比会出现异常。

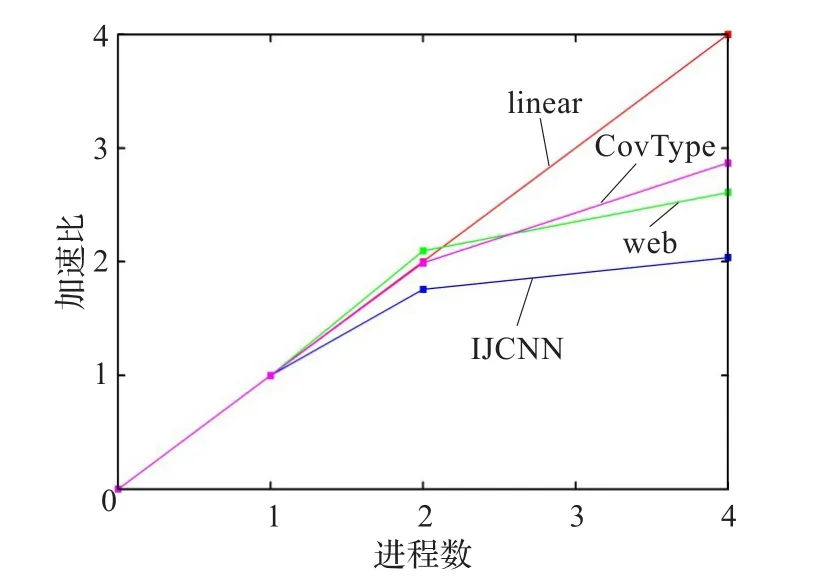
图4 RF-CCASVM算法加速比

最后，还将RF-CCASVM算法与目前已有的其他并行算法进行比较。实验对比P-packSVM[5]，PSVM[4]，PSSVM[15]算法在Adult和Web数据集上的预测准确率。这三种并行算法均是在计算机集群或大型服务器上完成的，实验结果由算法的作者在文章中提供。RF-CCASVM在两个数据集上的实验结果分别是在采样特征D=3 000和D=200时得到的。实验结果表明，RF-CCASVM算法能在有限资源上解决大规模的学习问题，并能获得与运行在大集群并行环境下的并行学习算法相当的预测能力。

6 结束语

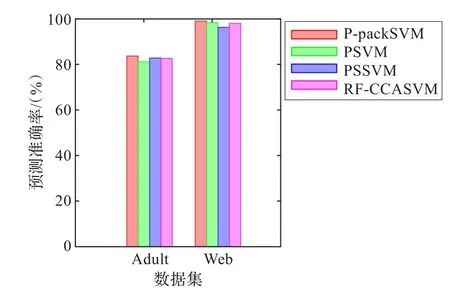
图5 RF-CCASVM与其他并行算法预测能力比较

提出了一种资源有限的大规模并行SVM算法。应用随机傅里叶特征来一致近似核函数，进而在随机傅里叶特征空间上训练线性SVM。该并行算法的时间复杂性为O(lD lb(1/ϵ)/m)。理论分析与实验结果表明，该并行算法可在有限的计算资源条件下，高效求解大规模SVM，并保证较高的预测精度，是正确的、有效的。

进一步工作将研究随机特征采样维度D的选取方法，给出理论界、计算开销和可保证的预测精度。

[1]Vapnik V.The nature of statistical learning theory[M].New York：Springer-Verlag，2000.

[2]Cao L J，Keerthi S S，Ong C J，et al.Developing parallel sequential minimal optimization for fast training support vector machine[J].Neurocomputing，2006，70（1）：93-104.

[3]Zanghirati G，Zanni L.A parallel solver for large quadratic programs in training support vector machines[J].Parallel Computing，2003，29（4）：535-551.

[4]Chang E Y，Zhu Kaihua，Wang Hao，et al.Parallelizing support vector machines on distributed computers[C]//Advances in Neural Information Processing Systems.Cambridge：MIT Press，2008：257-264.

[5]Zhu Z A，Chen Weizhu，Wang Gang，et al.P-packsvm：parallel primal gradient descent kernel SVM[C]//Proceedings of the 9th IEEE International Conference on Data Mining.Piscataway：IEEE Press，2009：677-686.

[6]Collobert R，Bengio S，Bengio Y.A parallel mixture of SVMs for very large scale problems[J].Neural Computation，2002，14（5）：1105-1114.

[7]Graf H P，Cosatto E，Bottou L，et al.Parallel support vector machines：the cascade SVM[C]//Advances in Neural Information Processing Systems.Cambridge：MIT Press，2005：521-528.

[8]Hazan T，Man A，Shashua A.A parallel decomposition solver for SVM：distributed dual ascend using fenchel duality[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition.Piscataway：IEEE Press，2008：1-8.

[9]Forero P A，Cano A，Giannakis G B.Consensus-based distributed support vector machines[J].Journal of Machine Learning Research，2010，11：1663-1707. [10]Rahimi A，Recht B.Random features for large-scale kernel machines[C]//Advances in Neural Information Processing Systems.Cambridge：MIT Press，2008：1177-1184.

[11]Bǎzǎ E G，Li Fuxin，Sminchisescu C.Fourier kernel learning[C]//Proceedings of the 12th European Conference on Computer Vision.Berlin：Springer，2012：459-473.

[12]Li Fuxin，Ionescu C，Sminchisescu C.Random Fourier approximations for skewed multiplicative histogram kernels[C]//Proceedings of the 32nd DAGM Conference on Pattern Recognition.New York：Springer-Verlag，2010：262-271.

[13]Rudin W.Fourier analysis on groups[M].New York：JohnWiley & Sons，1990.

[14]Hsieh Cho-Jui，Chang Kai-Wei，Lin Chih-Jen，et al.A dual coordinate descent method for large-scale linear SVM[C]//Proceedings of the 25th International Conference on Machine Learning.New York：ACM，2008：408-415.

[15]Roberto D M，Harold Y M B，Ángel N V.Parallel semiparametric support vector machines[C]//Proceedings of the 2011 International Joint Conference on Neural Networks. Piscataway：IEEE Press，2011：475-481.

LIAO Shizhong, LU Wei

School of Computer Science and Technology, Tianjin University, Tianjin 300072, China

Support Vector Machines（SVMs）have become popular classification tools, but when dealing with very large datasets, SVMs need large memory requirement and computation time. Therefore, large-scale SVMs are performed on computer clusters or supercomputers. A novel parallel algorithm for large-scale SVM is presented. The algorithm is performed on a resource-limited computing environment and guarantees a uniform convergence. The infinite-dimensional implicit feature mapping of the Gaussian kernel function is sufficiently approximated by a low-dimensional feature mapping. The kernel SVM is approximated with a linear SVM by explicitly mapping data to low-dimensional features using random the Fourier map. The parallelization of the algorithm is implemented with a consensus centre adjustment strategy.Concretely, the dataset is partitioned into several subsets, and separate SVMs are trained on processors parallel with the subsets. When the optimal hyperplanes on subsets are nearly found, solutions achieved by separate SVMs are replaced by the consensus centre and are retrained on the subsets until the consensus centre is optimal on all subsets. Comparative experiments on benchmark databases are performed. The results show that the proposed resource-limited parallel algorithm is effective and efficient.

parallel Support Vector Machines（SVM）; large-scale datasets; limited resource; random Fourier features;consensus centre adjustment

LIAO Shizhong, LU Wei. Support vector machine via consensus centre adjustment on random features. Computer Engineering and Applications, 2014, 50（17）：44-48.

A

TP181

10.3778/j.issn.1002-8331.1308-0145

国家自然科学基金（No.61170019）；天津市自然科学基金（No.11JCYBJC00700）。

廖士中（1964—），男，博士，教授，研究领域为人工智能应用基础、理论计算机科学；卢玮（1989—），女，在读硕士研究生，研究方向为核方法、并行算法。E-mail：szliao@tju.edu.cn

2013-08-13

2013-10-08

1002-8331（2014）17-0044-05

CNKI网络优先出版：2013-11-25,http://www.cnki.net/kcm s/detail/11.2127.TP.20131125.1535.015.htm l