基于听觉外围模型的音频基频估计方法

刘鑫，鲍长春

北京工业大学电子信息与控制工程学院，北京 100124

基于听觉外围模型的音频基频估计方法

刘鑫，鲍长春

北京工业大学电子信息与控制工程学院，北京 100124

针对音频信号中的暂态成分对基频检测可靠性的影响，提出了一种基于听觉外围模型的基频估计方法。该方法根据听觉外围模型来模拟声音在人耳内耳听觉神经上传导过程，并利用循环平均幅度差函数判断每个神经传导信号上呈现的时域周期性，进而提取音频信号的基频。实验结果表明，在纯净音频条件下，该方法能准确地估计出音频信号的基频，并且在不同音量打击乐信号的干扰下，所提方法的平均错误率低于三种参考方法。

基频估计；听觉外围模型；循环平均幅度差函数

1 引言

基频定义为语音和音调性音乐等准周期信号的最低频率，其倒数为信号周期，描述了发声体振动所引起的周期性特征[1-2]。在语音与音频信号的压缩编码、语音分析合成以及音频信息检索等应用中，基频估计直接决定了系统的最终性能。为此，研究人员针对纯净音频相继提出了众多的基频估计方法[2-8]。然而在噪声条件下，基频估计的性能还有待进一步提升，特别是背景声中打击乐所蕴含的暂态成分严重影响着基频估计的可靠性。为此，本文针对打击乐干扰下音调性器乐信号的基频估计问题展开研究。

传统的基频估计方法通常分为时域估计法、频域估计法和时频联合估计法。由于时域估计法具有较高的计算效率，该方法在语音与音乐信号的基频检测中得到了广泛的研究。其中，平均幅度差函数（Average M agnitude Difference Function，AMDF）法与自相关函数（Autocorrelation Function，ACF）法在准确度以及鲁棒性方面都具有良好的性能，被广泛应用于语音与音频编码系统中[2]。近年来，有学者在此基础上分别利用循环AMDF[3]、加权ACF[4]来改善传统时域基频估计的准确性。而Cheveigne等根据累积幅度差函数提出了YIN方法[5]，在附加不同噪声成分的条件下降低了基频估计的总错误率。此外，也有学者在时域估计的基础上借助音频频谱上的谐波相关性修正基频[6-8]，进而在外加白噪声和babble噪声条件下有效地提取出音频信号的基频。在实际音频信号中，打击乐器的伴奏会严重影响音调性器乐或者人声演唱音频信号基频估计的准确性。这类暂态性声音具有时域突变性，除了在特定频段存在较高能量的非谐波性成分外，还会在全频带上形成类噪声性频谱。这样的暂态干扰下，如何获得可靠的基频估计就成为了一个具有挑战性的问题。

基频感知理论[9-11]表明，人耳对声音基频的感知并不完全等同于准周期信号的振动频率，而是声音的主观心理声学属性。在含噪或者暂态干扰的条件下，尽管信号的周期性受到了严重的破坏，人耳仍能够感知到声音的基频。为此，有学者[9-10]针对人耳外围声学系统展开研究，以图通过分析在人耳基底膜上听觉神经动作电位的时间结构来确定声音信号的感知基频。受此启发，本文提出了一种基于听觉外围模型的音频基频估计方法，用于在打击乐干扰下提取音调性器乐信号的基频。该方法首先根据听觉外围模型[9，11]将音频信号分解到不同的临界频带中，有效地分散了暂态干扰信号对音频信号时间相关性的影响。接下来，通过一系列非线性处理来模拟声音在人耳内耳听觉神经上传导过程，借助其蕴含的积分特性抑制了各个临界带上的暂态干扰。最终，利用循环AMDF判断每个神经传导信号上呈现的时域周期性，进而提取音频信号的基频。实验结果表明，相比于参考方法，所提方法有效地改善了在暂态干扰下器乐信号基频估计的准确性。

2 基于听觉外围模型的基频估计算法

所提出基频估计方法的原理如图1所示。该方法可粗略地划分为四个部分：（1）听觉外围模型；（2）基于循环AMDF的基频粗估计；（3）后处理；（4）精细搜索。首先，利用Meddis听觉外围模型模拟各个临界带上听觉神经的传导过程，获得神经刺激信号。由于该信号与基频感知直接相关，因此本文利用循环AMDF来分析各个神经信号的时域周期特性。接下来，将各个临界带的时域结构拟合起来，结合基频增强方法实现对音频信号周期的粗估。最终，借助抛物线内插，进一步提升基频检测的精确度。下面将针对各个部分逐一进行介绍。

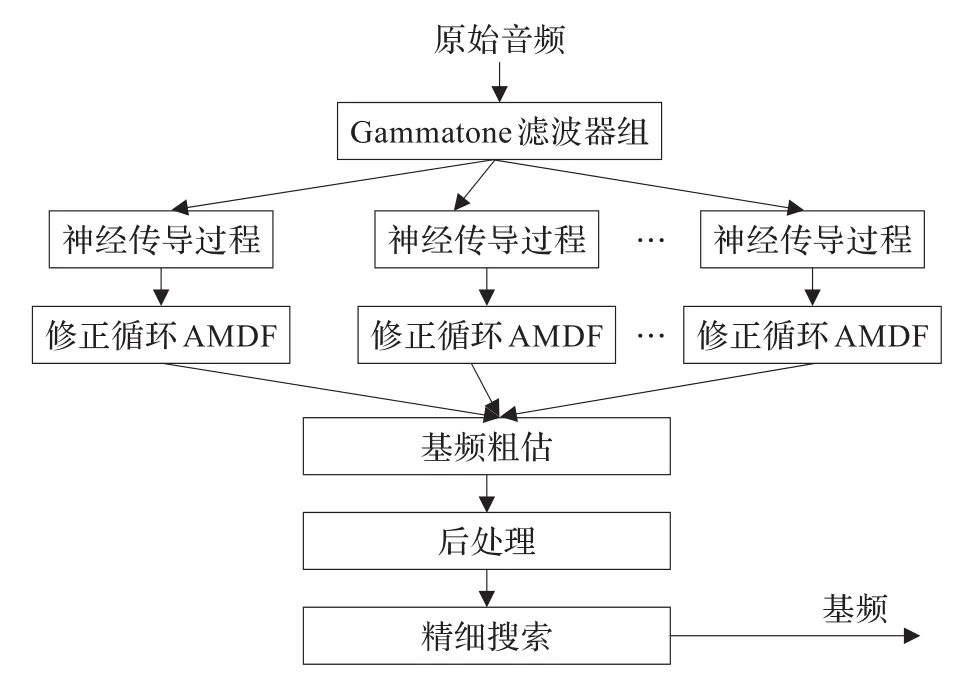
图1 基于听觉外围模型的基频估计方法原理框图

2.1 听觉外围模型

听觉外围模型能够模拟声音信号在人耳耳蜗基底膜上传导机制和内耳毛细胞的神经传导过程，进而分离出听觉神经刺激信号。相关听觉研究表明[10]，该信号与原始音频具有相同的周期性，因此可用于分析音频信号的基频。

2.1.1 Gamm atone滤波器组

令输入信号为32 kHz采样、14 kHz带宽的宽带音频x(i)，i=0，1，…，N，N=640对应20 m s的分析帧长。听觉外围模型首先采用Gammatone滤波器组在100 Hz～ 10 kHz频率范围内将x(i)分解到25个临界带上，从而模拟了耳蜗基底膜上特定位置受声音信号刺激后发生的波动现象。每个Gammatone滤波器采用4阶线性带通滤波器实现，其中心频率均匀分布在等效矩阵带宽尺度下。各个滤波器的带宽会随其中心频率的上升逐渐增加。这样，第j个频带的Gammatone滤波器的输出值xg(j，i)可描述基底膜特定位置上所受到的听觉刺激，如下式所示：

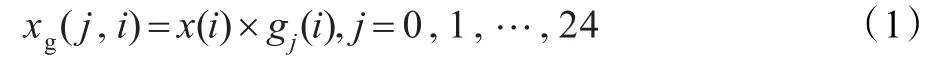
其中，gj(i)表示第j个Gammatone滤波器的脉冲响应。

2.1.2 内耳毛细胞模型

声音信号经过Gammatone滤波器组后，转化为各个临界频带上基底膜所接收的听觉刺激。根据Meddis内耳毛细胞模型[9]，内耳毛细胞在受到这些刺激后会释放自由传导物质，触发听觉神经纤维产生电信号，进而传导到听觉神经中枢中，其具体过程如图2所示。

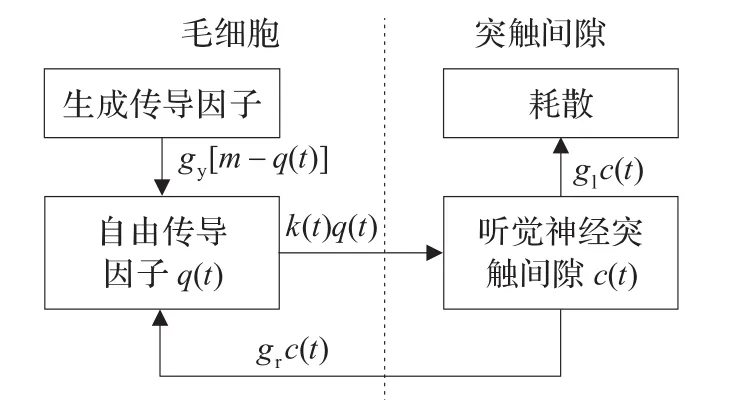
图2 Meddis内耳毛细胞模型原理框图

假设毛细胞内包含一定量的自由传导物质，并以一定速率释放到听觉神经突触间隙中。设t时刻毛细胞中自由传导物质的数量为q(t)，其释放速度k(t)与接收到听觉刺激的幅度xg(t)有关，如下式所示：

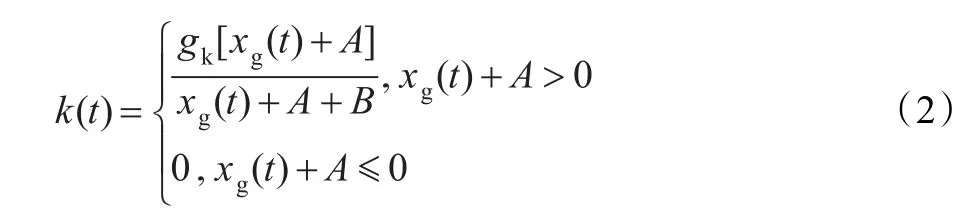
其中，gk、A、B均为正整数。由上式可见，当没有听觉刺激存在时，自由传导物质仍以gkA/(A+B)的速率释放。那么，在d t时间段内释放的自由传导物质数目为k(t)q(t)d t，而在内耳毛细胞内还会补充一定的传导物质gy[m-q(t)]d t。若神经突触间隙中自由传导物质的数量为c(t)，则会有数目为grc(t)d t的传导物质返回到毛细胞，而数目为glc(t)d t的传导物质则将耗散掉。将以上过程总结为动态系统可表示为：

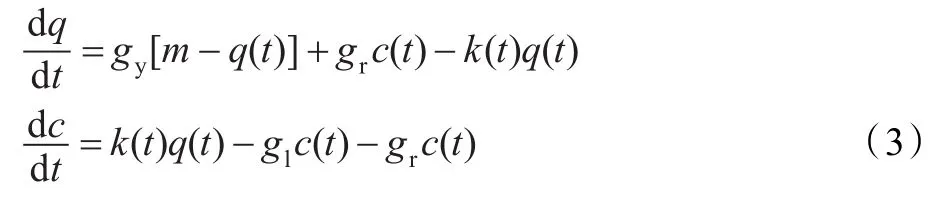
最终，根据接收到听觉刺激xg(t)的强度可以动态地控制传导物质在内耳毛细胞和听觉神经突触间隙间的双向传导。根据Meddis听觉研究结果[11]，内耳毛细胞模型中的相关参数分别设置为：m=1；A=5；B=300；gk=200；gy=5.05；gl=2 500；gr=6 580。相关听觉实验表明，在突触间隙中传导物质的数目c(t)与听觉神经上产生电信号的概率成正比，且其周期性与人耳对音频信号的主观基频感知相关，那么可以将式（3）所示的连续动态系统离散化，并得到各个临界带的神经刺激信号离散时间序列c(j，i)。

以某一段响板干扰下的口琴音频信号为例，图3和图4分别表示其时域波形及听觉外围模型各个通道输出的听觉刺激波形。在时域波形中，响板信号的幅度超过了口琴信号的幅度，严重影响到该信号的周期性。利用听觉外围模型进行处理后，响板信号随着口琴音频一起分解到不同的听觉通道中，其时间暂态特性被大大的削弱了。由图4可知，前10个通道的听觉刺激信号基本上没有受到响板信号暂态成分的过多影响，而在高频通道中，响板信号的暂态干扰仅仅改变了听觉刺激的时间包络信息，对其周期性的干扰作用十分有限。因此，可以看出利用听觉外围模型对音频信号进行分解，能够有效地抑制暂态成分对基频感知的消极影响。

根据基频感知原理，人耳基底膜上听觉激励的周期性与声音信号的基频息息相关。为此可以通过分析各个通道下听觉刺激信号的周期特性，进而实现对原始音频信号基频的有效估计。

2.2 循环AMDF

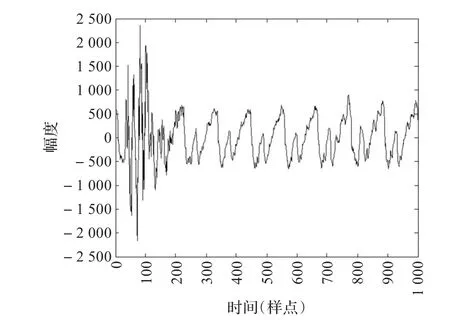
图3 响板干扰下口琴音频的时域波形

本文利用循环AMDF方法对各个临界带上神经刺激信号的周期性进行分析。该方法借助循环移位法，降低当前信号与其多倍周期延迟信号的相关性，进而有效抑制信号时频包络浮动所造成的周期加倍现象[3]。对于第j临界带下神经刺激信号c(j，i)，其循环AMDF可以表示为：

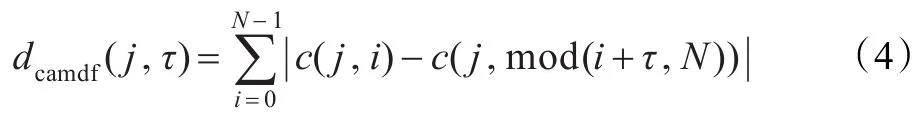
其中，τ为时间延迟，N=640为音频信号的分析帧长，mod(i+t，N)表示i+τ模N的余数。

为了初步判定音频信号的周期，定义各个临界带下循环AMDF值dcamdf(j，τ)和dscamdf(τ)作为本段音频的总循环AMDF，如下：

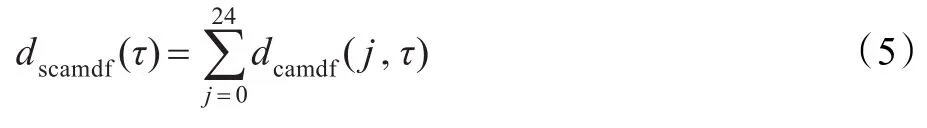
最终，根据总循环AMDF曲线判定音频信号的周期。

同样以响板干扰下口琴音频信号为例，听觉外围模型各个通道输出听觉刺激波形的循环AMDF曲线和总循环AMDF曲线如图5、图6所示。可见，尽管响板干扰对口琴音频的时域干扰比较强烈，但是经过听觉外围模型，其暂态成分分解到各个临界带通道上，因而对各个通道听觉刺激信号周期性的影响并不显著。并且循环AMDF方法利用循环移位技术降低了较大延迟下信号的相关性，有效地抑制了周期加倍的现象。因此，利用简单的最小值搜寻方法很容易在总循环AMDF曲线上确定真实周期，即τ=112。图7描述的是对原始音频信号时域波形进行处理后得到的循环AMDF曲线，可见由于响板信号的暂态特性严重影响到了口琴信号时域波形的周期特性，很难根据循环AMDF曲线确定真实的周期。

2.3 后处理

为了改善基频的稳定性，本文还会引入信号周期的历史值来对基频估计进行后处理。

令上一帧音频信号最终获得的周期估计值为Pold，则可在总循环AMDF曲线上以τ=Pold为中心加以一个对称窗函数来减小Pold附近的幅度差函数值，进而实现基频增强。对称窗函数定义为：

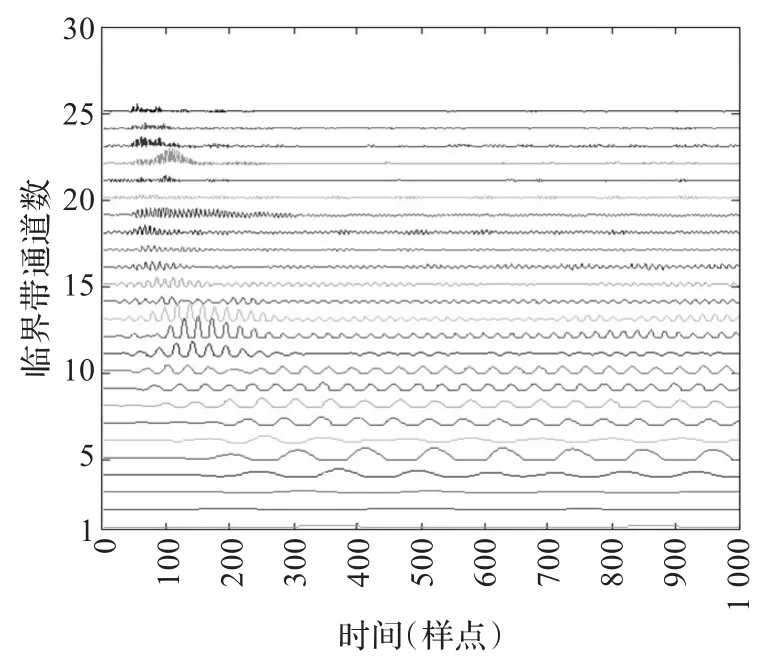
图4 听觉外围模型各个通道输出的听觉刺激波形

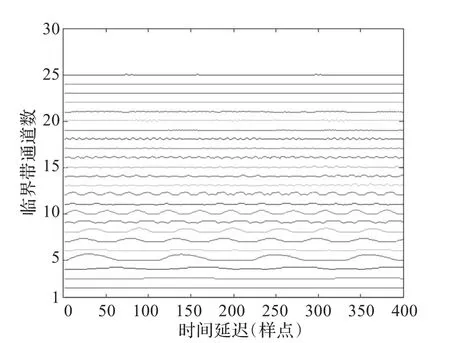
图5 听觉外围模型各个通道的循环AMDF曲线

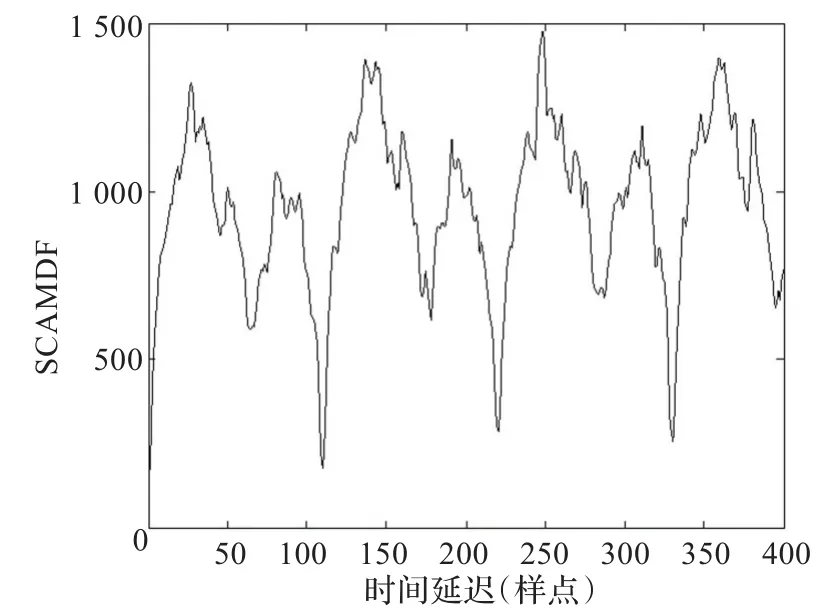
图6 总循环AMDF曲线

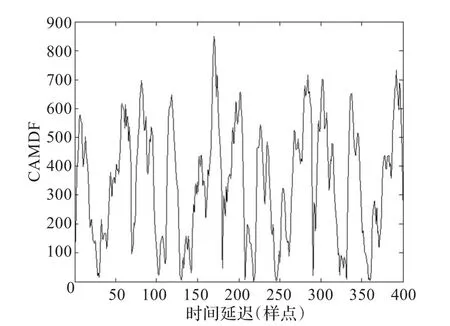
图7 时域波形对应的循环AMDF曲线

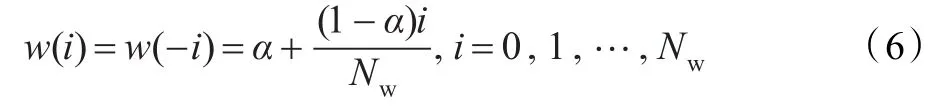
其中，α决定了窗中心位置的函数值，并与前一帧音频的谐波程度相关。若前一帧信号为强谐波信号则α=0.9，否则α=1，即不对周期历史进行增强。随着与窗中心位置逐渐远离，对称窗函数的值将趋近于1。根据实验结果，当Nw=5时，基频增强的效果最好。

接下来，在基频增强后总循环AMDF首次达到极大值后的延迟范围内，找出该曲线的最大值dmax和最小值dmin，并确定阈值为T=dmin+0.05(dmax-dmin)。在总循环AMDF值小于阈值T的范围里，搜索第一个局部极小值，并判定其所在时间延迟位置为周期P。

2.4 精细搜索

为了提升基频估计的精度，本文所提方法还需要进一步在整数周期P附近确定分数周期。首先，在[P-3，P+3]范围内，以1/4的时间延迟为分辨率对原始的总循环AMDF进行抛物线内插。然后，选择该范围内插值后总循环AMDF的最小值。最终，以该延迟作为最终的分数周期Pfin，其倒数则表示音频信号的基频。

3 实验测试与结果

3.1 测试样本

为了评价本文所提方法的基频估计性能，本文选择欧洲广播联盟录制的声音质量评测材料[12]中的4种典型音调性器乐（短笛、钢琴、小号、小提琴）和3种打击乐信号（响板、低音鼓、铙钹）作为测试样本。其中，短笛和钢琴信号低频谐波相对丰富，而高频能量衰减较快。小号和小提琴信号在全频带上均存在丰富的谐波，且小提琴信号具有明显的颤音结构。而3种打击乐都具有清晰的暂态特性。响板信号在时域上收敛较快，具有一定的音调性，而低音鼓和铙钹信号收敛较慢，且在4 kHz以上的频段中铙钹的能量要明显高于低音鼓。

测试前，需要去除所有信号中的静音段，且每种音调性器乐演奏时分别附加不同的打击乐信号，构成含噪音频，进而在不同的器乐与打击乐平均功率比下对所提基频估计方法的鲁棒性进行研究。最终，获得的36段测试样本采样频率为32 kHz，有效带宽为14 kHz，长度在10 s左右。基频估计过程中所选用的分析帧长为20 ms，帧间无交叠。所有音频的真实基频通过人工标注的方法确定，其分布在200～1 600 Hz范围内，即周期搜索范围为20～160。

3.2 参考算法

为了测试算法的有效性，本文所提出的基频估计算法将进一步与三种参考算法（AMDF法[2]、YIN法[5]和Meddis基频估计法[9]）进行比较。AMDF法采用了传统的AMDF来判定信号的周期；YIN法则引入累积均值归一化差函数来改进AMDF，提升了较小周期下基频估计方法的准确性；而Meddis基频估计法同样采用Meddis听觉外围模型并利用ACF衡量听觉刺激信号的周期性。为了公平起见，这三种参考方法采用与本文所提方法相同的后处理和精细搜索过程，并分别在纯净器乐信号和不同器乐与打击乐平均功率比下与本文所提方法进行基频估计的性能对比。

3.3 误差测度

令第n帧测试信号的真实周期为Ptrue(n)，由算法提取出的周期为Pest(n)，则基频估计方法的误差测度可根据基频误差e(n)得到，如下所示：

若某一帧的基频误差e(n)大于10 Hz，则认定该帧具有较大估计误差。对于整段音频信号，较大误差帧的数目占总帧数的比例可作为基频估计方法的总错误估计率。

3.4 纯净信号下基频估计性能

表1中显示了在纯净音频信号下不同基频估计方法的总错误率。结果表明，在不含噪声的条件下，AMDF法和Meddis法具有较大的总错误估计率，这主要是因为周期搜索范围比较宽，在不做特别优化的前提下，AMDF法和Meddis法容易出现周期加倍的现象。Yin法和本文方法有效地抑制了稳态信号下的周期加倍减半，并将总错误率控制在10%以内。但是在不同音调间的过渡阶段，两个不同周期的音调成分同时出现，这改变了音频时域信号的周期性，进而出现估计误差。

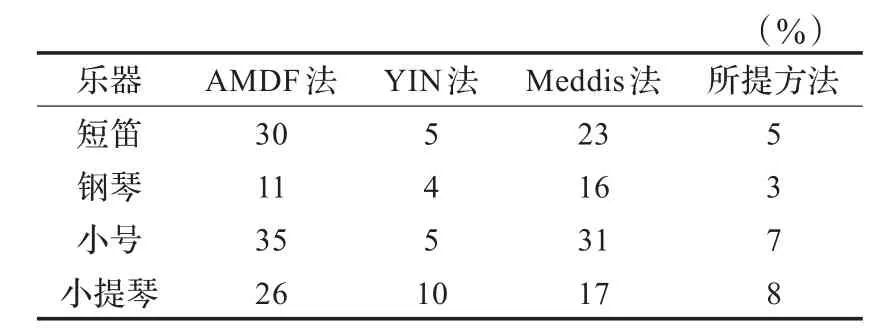
表1 不同基频估计法对纯净音频的总错误估计率

3.5 打击乐信号干扰下基频估计性能

在实际音频信号中，打击乐中的暂态成分会影响音调性器乐信号的基频估计。本文分别在两种器乐与打击乐平均功率比（20 dB和0 dB）下，利用钹铙、低音鼓、响板三种打击乐作为伴奏，构造成含噪音频。不同打击乐干扰下四种基频估计方法的总错误估计率如表2～表4所示。

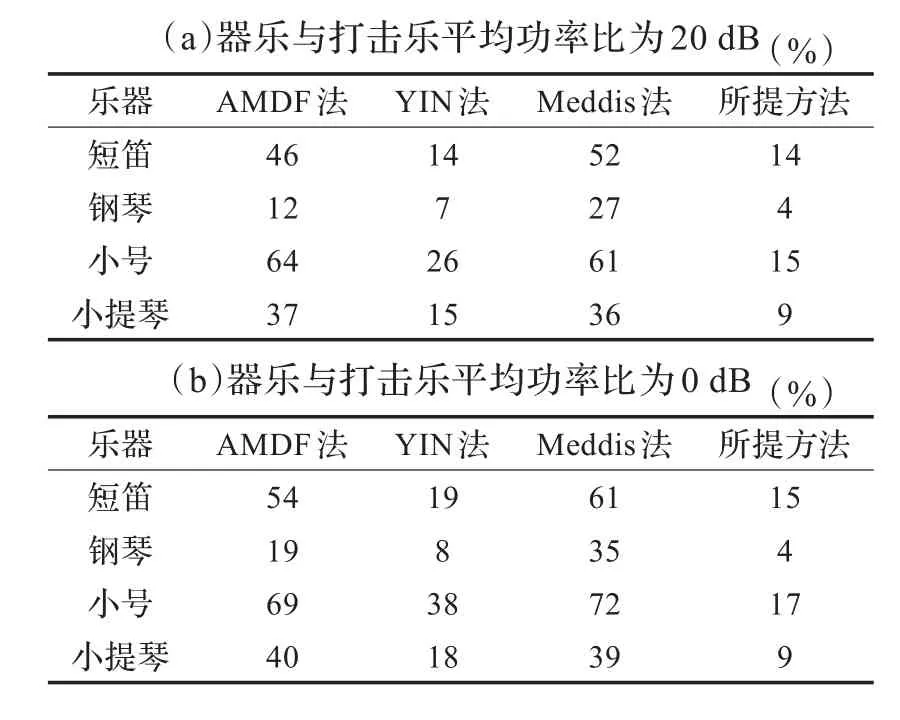
表2 在钹铙干扰下不同基频估计法总错误估计率

测试结果表明，受到打击乐信号的干扰，AMDF法和Meddis法相比于纯净信号条件下总错误估计率平均上升10%～20%，且器乐与打击乐平均功率比为0 dB时，这两种方法的平均总错误估计率进一步上升到40%以上。而YIN法和本文方法错误估计率在10%～20%，且随着器乐与打击乐平均功率比上升，本文方法总错误估计率小幅上升，并比YIN法的错误率低5%～10%。此外，从测试结果中还可以看出，钢琴信号受到打击乐干扰时，总错误估计率上升幅度比另外三种器乐信号要小，这主要是因为键盘乐器相比于管弦乐器起振时间短，且中低频谐波丰富而稳定，无明显颤音结构。在受到暂态噪声干扰时，利用后处理方法能够有效增强基频轨迹的连续性。

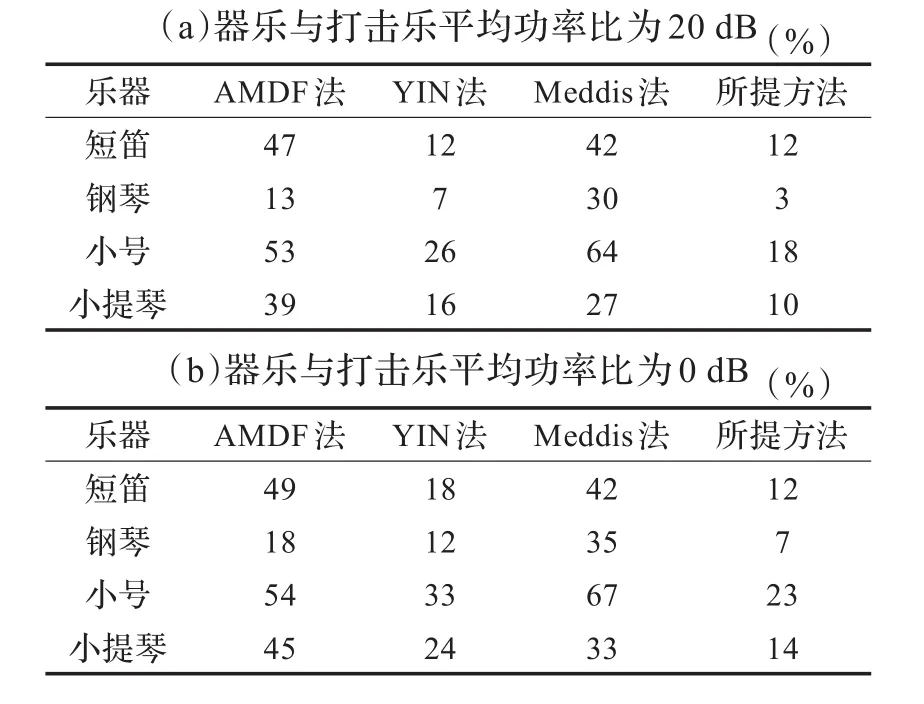
表3 在低音鼓干扰下不同基频估计法总错误估计率

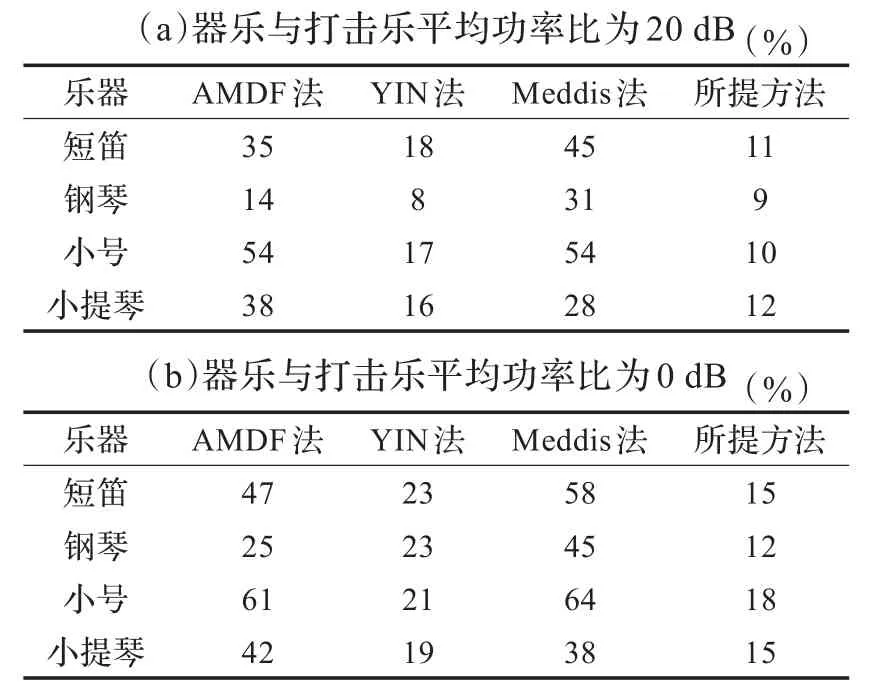
表4 在响板干扰下不同基频估计法总错误估计率

综上所述，打击乐信号会明显干扰音调性器乐音频的基频，而本文方法估计基频的总错误率要低于三种参考方法。

4 结论

本文提出了一种基于听觉外围模型的音频信号基频估计方法。该方法借助Meddis听觉外围模型和循环AMDF来估计音调性器乐信号的基频。测试结果表明，在纯净音频条件下本文提出方法有效地抑制了信号周期加倍减半现象，并准确地估计出音频信号的基频；在不同能量水平打击乐信号的干扰下，本文方法基频估计的平均错误率仍能控制在20%以下，并优于三种参考方法。

[1]Vary P，Martin R.Digital speech transmission-enhancement，coding and error concealment[M].UK：John Wiley & Sons Ltd，2006.

[2]Hess W.Pitch determination of speech signals[M].New York：Springer-Verlag，1983.

[3]Zhang W，Xu G，Wang Y.Pitch estimation based on circular AMDF[C]//IEEE International Conference on Acoustics，Speech，and Signal Processing，Orlando，USA，2002，1：341-344.

[4]Shimamura T，Kobayashi H.Weighted autocorrelation for pitch extraction of noisy speech[J].IEEE Transactions on Speech and Audio Processing，2001，9（7）：727-730.

[5]Cheveigné A D，Kawahara H.YIN，a fundamental frequency estimator for speech and music[J].The Journal of the Acoustical Society of America，2002，111（4）：1917-1930.

[6]Zahorian S A，Hu H.A spectral/temporal method for robust fundamental frequency tracking[J].The Journal of the Acoustical Society of America，2008，123（6）：4559-4571.

[7]Shahnaz C，Zhu W P，Ahmad M O.A pitch extraction algorithm in noise based on temporal and spectral representations[C]//IEEE International Conference on Acoustics，Speech and Signal Processing，Las Vegas，Nevada，USA，2008：4477-4480.

[8]Hsu C L，Wang D L，Jang J S R.A trend estimation algorithm for singing pitch detection in musical recordings[C]//IEEE International Conference on Acoustics，Speech and Signal Processing，Prague，Czech Republic，2011：393-396.

[9]Meddis R.Simulation of mechanical to neural transduction in the auditory receptor[J].The Journal of the Acoustical Society of America，1986，79（3）：702-711.

[10]Rao P，Shandilya S.On the detection of melodic pitch in a percussive background[J].Journal of the Audio Engineering Society，2004，52（4）：378-390.

[11]Meddis R，Hewitt M J，Shackleton T M.Implementation details of a computation model of the inner hair-cell/auditory-nerve synapse[J].The Journal of the Acoustical Society of America，1990，87（4）：1813-1816.

[12]EBU.Tech 3253 Sound quality assessment material recordings for subjective tests[S].Geneva：EBU，2008.

LIU Xin,BAO Changchun

School of Electronic Information and Control Engineering, Beijing University of Technology, Beijing 100124, China

The transient components of audio signals may reduce the reliability of fundamental frequency estimation. A fundamental frequency estimation method based on auditory peripheral model is proposed in this paper. The auditory peripheral model is adopted to mimic the transduction in the auditory nerve of the inner hair cells, and a circular average magnitude difference function is used to judge the periodicity of the response of auditory nerve for estimating the fundamental frequency of audio signals. Experimental evaluations show that the proposed method can accurately estimate the fundamental frequency of the clean audio signals. With the percussive interference in different volumes, the proposed method also achieves a lower error rate in comparison with three reference methods.

fundamental frequency estimation;auditory peripheral model;circular average magnitude difference function

LIU Xin, BAO Changchun. Fundamental frequency estimation method for audio signals based on auditory peripheral model. Computer Engineering and Applications, 2014, 50（17）：29-33.

A

TN912.3

10.3778/j.issn.1002-8331.1403-0174

国家自然科学基金（No.61072089）。

刘鑫（1986—），男，博士研究生，研究领域为语音与音频信号处理；鲍长春（1965—），男，博士，教授，博士生导师，研究领域为语音与音频信号处理。E-mail：chchbao@bjut.edu.cn

2014-03-14

2014-04-28

1002-8331（2014）17-0029-05

CNKI网络优先出版：2014-05-05,http://www.cnki.net/kcms/doi/10.3778/j.issn.1002-8331.1403-0174.htm l