Hurst指数估计法的比较和研究

赵彦仲，吴立文

兰州理工大学计算机与通信学院，兰州 730050

Hurst指数估计法的比较和研究

赵彦仲，吴立文

兰州理工大学计算机与通信学院，兰州 730050

针对时间序列的Hurst指数的估计方法的问题，目前国内外已经提出了R/S，DAF，绝对值法，周期图法等多种方法。但上述方法都会对Hurst指数的估计值产生易误解和不一致的结果。针对这个问题，通过对R/S分析法，小波分析法，迭代估计算法和W hittle法的描述，进行数值模拟来说明这些方法所得Hurst指数估计值的误差，通过比较能够得出Whittle法是一种具有更高精度和更好稳定性的方法。

分形布朗运动；改进Whittle法；R/S；小波分析法；迭代估计法

1 引言

分形与混沌理论作为非线性科学中的两个重要组成部分，从上世纪70年代起在经济、金融研究中得到广泛的应用，其中估计经济学中时间序列曲线的Hurst指数H值就是其中之一[1]。Hurst等人曾证明，对应于不同的Hurst指数H(0＜H＜1)，存在以下情况：（1）H=0.5，是相互独立，方差有限的随机序列；（2）0.5＜H＜1，表明该序列有长程依赖性，即表现为持续性，且H越接近1，持续性越强；（3）0＜H＜0.5，表明该时间序列具有长程依赖性，且将来总体趋势与过去相反，这种现象称为反持续性，H越接近于0，反持续性越强，而其中随机性成分越少。到目前为止，国内外学者已经提出了多种估计Hurst指数的方法。其中Hurst提出了重极标差（R/S）分析法，以判断时间序列数据遵从随机游走是有偏随机游走过程的指标，并由Mandelbrot于1971年应用到金融时间序列分析中，成为应用于时间序列的分形特征的有效方法之一；Lo在经典R/S分析法的基础上给出了修正的R/S分析法（简称MR/S），从而克服了经典R/S分析法无法分辨短期相关性与长期相关性的缺点[2]；Giraitis等提出了样本序列累积离差的方法，更具稳健性和有效性[3]。Peng等在研究DNA组织时扩展了普通的波动分析方法，得到了DFA方法，它在消除时间序列局部趋势及发现局部相关方面比R/S及MR/S方法更优[4]。在Hurst指数估计方法中，R/S分析法是最常用的方法，后来很多学者又提出了小波分析法，迭代估计算法等方法能够更好地克服估计的周期长，误差大等问题，特别是有些方法在周期存在的情况下错误地检测到序列中存在的长依赖性[5]。可见在时间序列中，周期及趋势项的存在对Hurst指数的估计影响很大，所以在分析之前，应对分析的时间序列进行预处理，以消除周期和趋势的影响。本文主要针对就混沌，分形金融领域的股票市场中估计Hurst指数时所涉及到的分形维数计算的数学基础与方法进行详细讨论[6]。虽然很多学者对中国股市的有效性和长记忆性进行了多方面的分析，但他们均是对中国股市的总体有效性进行的研究，都得出了中国金融市场是一个弱式有效市场的结论，但关于中国自证券交易市场成立运行以来，其20多年的市场发展状态少有人研究。近年来，对于金融市场中Hurst指数的估计的研究，陆续有一些学者利用一些估计方法去估计，但是很少有人去比较这些估计结果，而Whittle分析法作为一种更稳定，更有效的分析法亦鲜有人研究[7]。本文最后就各类分形维数的数学定义，以金融市场中沪市，深市股票指数为例，相互联系及以各自特点进行比较详细的分析，并对就时间序列数据所广泛使用的关联维数，对Hurst指数的理论与估算方法进行研究[8]。

2 Hurst指数估计方法

针对Hurst指数的估计，本章主要介绍四种Hurst指数估计方法，包括基于极大似然whittle估计法，R/S分析法，小波分析法和迭代估计算法。

2.1 Whittle估计法

Whittle[9]估计法作为一种参数估计方法，更适合于统计推断，而且更高效。Whittle估计值，可以通过一下方法得到。

2.2 R/S分析法

R/S[10-11]分析法是现在估计Hurst指数最常用的一种方法，R/S分析法描述如下：

2.3 小波分析法

小波分析法[12-13]描述如下：

给定一时间序列Xi，i=1，2，…，n，对其进行二进制小波变换：

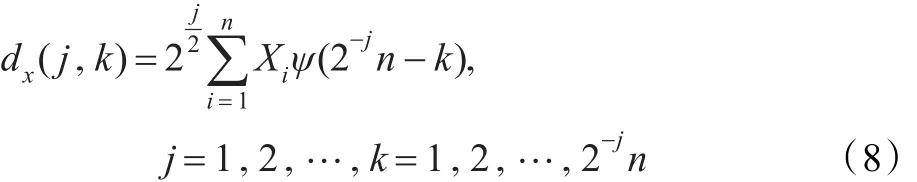
ψ(·)为母小波函数，dx(j，k)为小波变换系数，j为尺度参数，k为平移参数。若Xi为二阶平稳过程，则

f(v)和ψ(v)分别为Xi的功率谱和ψ(·)的傅里叶变换，而且

其中，c=lb[cfC(H，ψ)]。在(j，lbμj)的图上，用最小二乘法线性拟合得到的斜率为α=2H-1。

2.4 迭代估计算法

2.4.1 自相似的相关定义

定义1称为离散随机过程Xn的m阶聚集过程，如果它的k阶自相关系数记为ρm(k)。

定义2广义平稳的离散随机过程Xn称为自相似的，如果其m阶聚集过程与原过程Xn有相同的自相关系数结构，即ρm(k)=ρ(k)，对所有的m(=1，2，…)都成立，也就是说与Xn具有相同的二阶统计特性。

广义平稳的自相似过程的自相关函数满足：

2.4.2 迭代估计算法

网络流量序列Xt是自相似的，其中Xt表示在第i个时间周期内网络的业务量（字节数、包数量等），则其自相关函数ρk应该满足式（1），对该式进行变换得到H的迭代计算公式：

对于给定的序列X1，X2，…，Xn， 令

利用样本自相关函数代替ρk，有Hurst参数的迭代估计公式：

对于长相关过程，设初值=0.5。

式（17）成立的条件是k无穷大，然而实验证明，k取1不仅能够获得足够精度的Hurst估计值，而且能大大减少运算量。k取较大的值时迭代结果并不理想，导致这种情况的主要是随着k的增大，代替ρ所产生的误差对H估计值影响越来越大。因此，在式（17）中取k=1，得到简化的迭代估计公式：

由不动点定理可以证明该式在（0.5，1）区间内的收敛性和唯一性。

3 Hurst指数估计方法应用中存在的问题

本文对上述描述的几种方法中，应用最广泛的应属于R/S分析法。R/S分析法属于非参数分析法，不必假定潜在的分布是高斯分布，仅独立就可以。R/S分析法的研究对象不仅包括正态分布，而且也包括非高斯独立过程。

但是Taqqu等人指出了时间序列中周期存在对Hurst指数的估计有影响，周期越长，估计误差越大，特别是有些方法在周期存在的情况下，错误地检测到序列中存在的长程依赖性。估计Hurst指数，在监测信号中，对指出信号中非平稳性质，如均值变化，线性或多项式趋势对监测和估计长程依赖性的影响很大，在此情况下，R/S分析法估计结果差，易于非平稳性的具有短程依赖性过程混淆，而小波分析法的估计具有很好的鲁棒性。Hurst指数作为表征具有尺度不变和自相关函数缓慢衰减的特点，作为这一类数据统计特性的一个重要指标，它反映了数据的自相似程度及其二阶统计特性。小波的出现给这一问题带来了许多新的内容和方法，这是因为利用小波对信号分析是在尺度和时间域上进行的，尤其他的多尺度特性与自相似过程的尺度不变性有着自然的联系。与小波分析法相比，根据自相似过程的自相关函数的计算公式推导出一个估计Hurst指数的迭代公式，更加充分利用了已有信息，误差相对较小，并且该方法计算速度快，置信区间小，以及不易受时间尺度影响等优点。Whittle估计法，对长记忆性强弱Hurst指数的估计偏差最小，它是一种基于极大似然的参数估计法，该方法比前面提到的常用的几种方法更适合用于统计推断，而且更高效。可见，在时间序列中，周期及趋势项的存在对Hurst指数的估计影响很大，所以在分析之前，应对待分析的时间序列进行预处理，以消除周期和趋势项的影响，并且选择适当的方法估计Hurst指数。

4 实验结果与分析

4.1 数值模拟仿真方法的比较

由于目前对具体分形维参数还没有一个公认的估计值，因此本节采用蒙特卡罗仿真模拟，并取样本分别为350、500和1 000对上文介绍的各种Hurst指数估计方法进行实验比较和分析。对不同的Hurst指数值H和时间序列长度N，以及路径数Q，通过调用M atlab自带的wfbm(H，N)函数[9]产生Q条服从标准分数布朗运动的时间序列，记为(t=1,2,…，N;q=1，2，…，Q)。通过转化得到Q条服从分数高斯过程的时间序列应用上文介绍的方法对Q组时间序列Sq，t(q=1，2，…，Q;t=1，2，…，N)进行估计，得到Q个Hurst指数估计值Hq(q=1，2，…，Q)。则有其中，H为真实Hurst指数，ˆ为均值，σ为标准差，MSE为均方误差。通过这三个指标，得出数据估计结果如表1，通过图1，图2，图3的比较图形，能够分析估计结果的精确度、稳定性、无偏性等指标得出上一节提到的各种方法的比较分析是合理的。

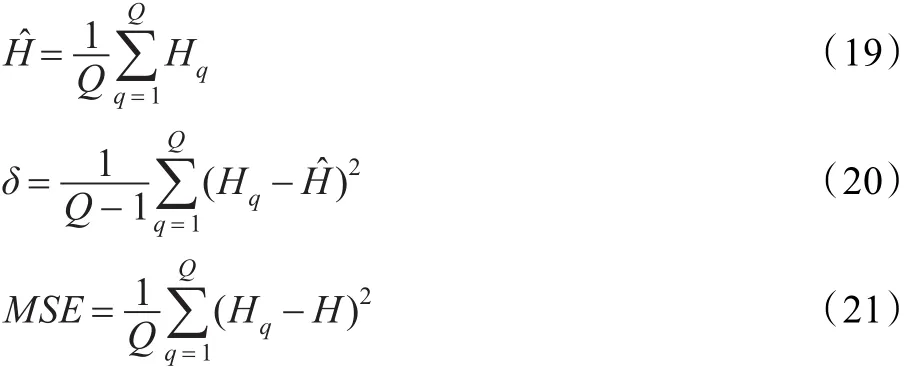
表2 各种方法的代号及名称

图1 当N=350时的结果

4.2 实验结果分析

通过描点，画出图1，2，3。从图1，当N=350时，可以看出Hurst指数真值一定，使用Whittle方法计算出的Hurst指数估计值最为稳定和准确。从图2，当N=500时，图3，N=1 000时，可以得出，使用Whittle方法相对其他方法更为精确、稳定。

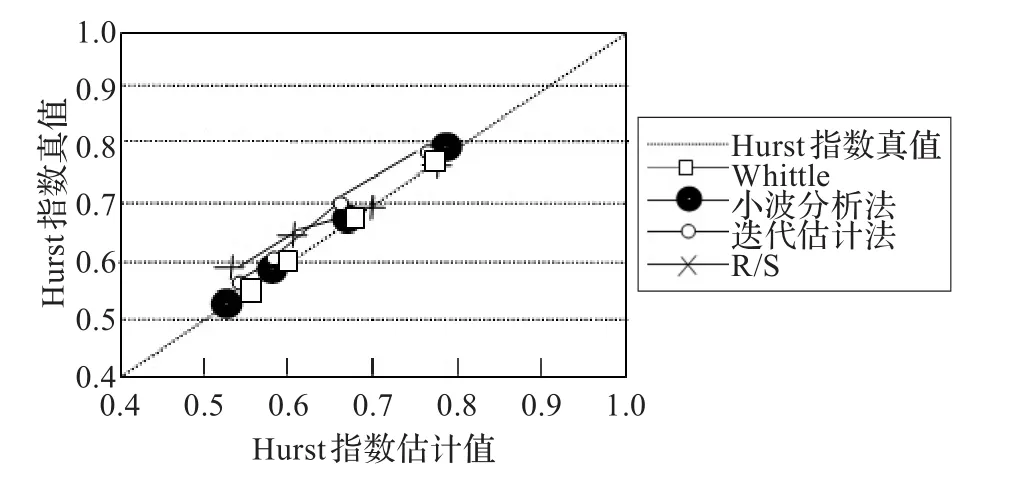
图2 当N=500时的结果

图3 当N=1 000时的结果

表3 上证指数和深圳指数收益率序列的基本统计特性1）

4.3 实验分析及应用

本节将采用蒙特卡罗仿真模拟证明精度和稳定性更好的Whittle方法进行实证分析应用。

4.3.1 数据选择及统计特性分析

鉴于我国学者多使用沪深两市股指数据进行长记忆性分析，为了方便比较分析，本文采用上证指数和深圳指数的日收盘价为研究对象，时间分别选取1990年11月19日至2011年2月14日和1991年5月3日至2011年1月14日，上证指数有4 904个样本，深圳指数有4 874个样本，数据来源于聚源数据库。对收益率yt=lbPt-lbpt-1，分别取其绝对值和平均值作为股市波动率的近似值为研究样本[15]。下面应用Whittle估计法分析上证指数和深圳指数的Hurst指数值。

4.3.2 使用W hittle法对上证指数和深圳指数进行的实验分析

表3上证指数和深圳指数的收益率序列和波动率序列的峰度和偏度值表明其均有别于正态分布。从J-B正态性检验结果来看，两只指数的J-B统计量均显著地超过了临界值，概率几乎为0。因此，两序列表现出尖峰，厚尾，右偏的特性，均为非正太分布。而ADF统计量的值表明沪深股指均为平稳时间序列。

5 结束语

针对Hurst值的估计，本文采用了四种方法，即Whittle、R/S分析法、迭代估计算法和小波分析法。通过蒙特卡洛仿真，使用这四种方法分别对Hurst指数进行了估计和比较。结果表明W hittle算法与国内常用的R/S分析法，迭代估计法和小波分析法这些方法相比较，Whittle估计法克服了这些方法的缺陷，使得估计值具有更高的精度和更好的稳定性，而且与均方根误差和标准差为指标说明了该方法的优越性，并进一步说明了Whittle算法对Hurst指数真实值以及样本大小敏感度方面的强壮性；而且在时间序列中，Hurst值的变化与样本容量有很大的关系，H值的总体规律是：随着消失矩增大，局部上H值时大时小，总体上H值在减小，消失矩越小，分解级数越大，求解的H值越准确。这一结果对未来的水蓄水量，食品价格，经济，金融包括医学等很多领域的研究提供了有价值的参考。

[1]孙霞，吴自琴.分形原理及其应用[M].合肥：中国科技大学出版社，中国科学技术大学出版社，2003.

[2]LAW Lang-termemory in stockmarket prices[J].Econometrica，1999，59.

[3]Giraitis L.Rescaled variance and related tests for long memory in volatility and levels[J].Journal of Econometrics，2003，112：265-294.

[4]Aqqu M S，Teverovsky V.Robustness of whittle type estimators for time serios with long range dependence[J]. Stochastic Model，1997，13：723-757.

[5]Montanari A，Taqqu M S.Teverovsky V.Estimating long-range dependence in the presence of periodicity：an empirical study[J].Mathematical and Computer Modelling，1999，29：217-228.

[6]史美景，邱长溶.分形金融市场特征及其应用[J].财经论坛，2005（4）：103-104.

[7]储海林，殷勤译.分形市场分析：将混沌理论应用到投资与经济理论上[M].北京：经济科学出版社，2002.

[8]林欣.基于赫斯特指数的股票风险研究[J].上海管理科学学报，2008（5）.

[9]Cpronopoulou A，Vien F.Hurst index estimation for selfsimilar processes with long-memory[C]//Dun J，Luo S，Wang C.Recent Development in Stochastic Dynamics and Stochastic Analysis.Singapore：World Scientific，2010.

[10]胡彦梅.中国股市长记忆的修正R/S分析[J].数理统计与管理，2006，25（1）：73-77.

[11]Adas A.Traffic models in broadband networks[J].IEEE Communications Magazine，2007，35（7）：82-89.

[12]任勋益，王汝传，王海艳.基于自相似检测DDOS V攻击的小波分析法[J].通讯学报，2006，27（5）：6-11.

[13]任勋益，王汝传，祁正华.小时矩阵对小波分析求解自相似数Hurst的影响研究[J].电子与信息学报，2007（9）.

[14]Abry P，Sellan F.The wavelet-based synthesis for the fractiond Brewnian motion proposed by F[J].Sellan and Y Meyer：Remarks Analysis，2006，3（4）：377-383.

[15]Osw iecimka P，Kwapien J，Drozdz S.Multifractality in the stock market：price increments versus waiting times[J]. Physica A，2005，347（1/2）：626-638.

ZHAO Yanzhong,WU Liwen

School of Computer and Communication,Lanzhou University of Technology,Lanzhou 730050,China

At present,there are many methods of analyzing the Hurst exponent of time series in and abroad,but most of them could lead to misunderstanding and disagreement to the estimation of Hurst exponent.This paper describes R/S analysis, wavelet analysis,iterative algorithm estimation and modified Whittle analysis,by the means of numerical simulation,to com pare the error of estimation of Hurst exponent that obtained by the above methods.The comparison is made to test and verify Whittle method has the best accuracy and stability.

fractal Brownian motion;improved whittle method;R/S;wavelet analysis;iterative estimation

A

TP393

10.3778/j.issn.1002-8331.1209-0141

ZHAO Yanzhong,WU Liwen.Comparison and application of estimation of Hurst exponent.Computer Engineering and Applications,2014,50（16）：154-158.

赵彦仲（1987—），男，硕士研究生，主要研究领域为分形几何及其应用；吴立文（1985—），男，硕士研究生，主要研究领域为分形几何及其应用。E-mail：kurekey@163.com

2012-09-15

2012-11-06

1002-8331（2014）16-0154-05

CNKI网络优先出版：2012-12-18,http://www.cnki.net/kcms/detail/11.2127.TP.20121218.1522.015.htm l