一类具有脉冲和时滞的细胞神经网络系统的反周期解
2014-07-07张林丽何莲花
张林丽,何莲花
(1.海口经济学院基础课部,海南海口571127;2.贵州师范大学数学与计算机学院,贵州贵阳550001)
一类具有脉冲和时滞的细胞神经网络系统的反周期解
张林丽1,何莲花2
(1.海口经济学院基础课部,海南海口571127;2.贵州师范大学数学与计算机学院,贵州贵阳550001)
利用迭代分析方法研究了一类具有脉冲和时滞的细胞神经网络反周期解的存在性和唯一性,以及平衡点的一致稳定性,得到了一些新的结论.
迭代分析方法;反周期解;脉冲;时滞
在神经网络动力学模型的研究中,细胞神经网络系统作为目前最流行的人工神经网络之一,被广泛地应用于生物、工程、信号与图像处理等不同领域.信号在传播和处理过程中不可避免地会受外界干扰和产生时滞现象,而脉冲和时滞往往是神经网络系统振动和不稳定的原因;同时,系统往往处于周期变化的环境下,其动力学呈现出周期性特征,因此,探讨神经网络的周期动力学行为具有实际意义.目前,对神经网络动力学的研究吸引了越来越多的关注[1-2],其中关于细胞神经网络系统周期解的理论和应用也得到了充分探讨[3-6],但研究具有脉冲时滞神经网络反周期解的文献尚不多见[7-10].本文利用迭代分析方法研究了一类具有脉冲和时滞的细胞神经网络系统反周期解的存在性、唯一性以及平衡点的一致稳定性.

本文考虑如下一类具有脉冲和时滞的细胞神经网络系统:其中,n是神经网络中神经元的个数;脉冲时刻tk满足表示在与神经网络不连通并且无外部附加电压差的情况下第i个神经元恢复静止状态下的速率表示第i个神经元在t时刻的状态表示第j个神经元在t时刻的输出作用于第i个神经元上的影响强度表示第j个神经元在t-τj时刻的输出作用于第i个神经元上的影响强度,并且τj0,表示第i个神经元在t时刻的沿第j个神经元的轴突信号传输时滞;表示在t时刻第j个神经元的输出量表示在t时刻第i个神经元的外部输入表示在固定的脉冲时刻tk所产生的爆破;是定义在上的一个实连续函数;

假设:(A1)存在T>0,对∀t,v∈R,有
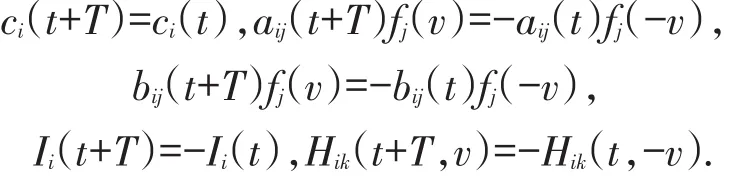
(A2)存在p∈Z+,有
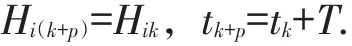

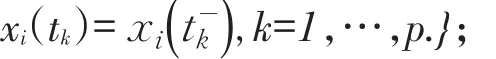

令

以及范数

那么P是一个Bɑnɑch函数空间.
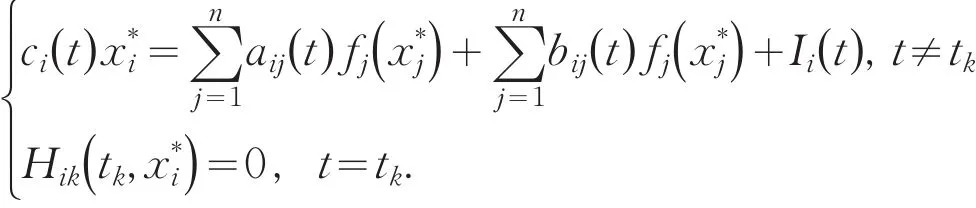
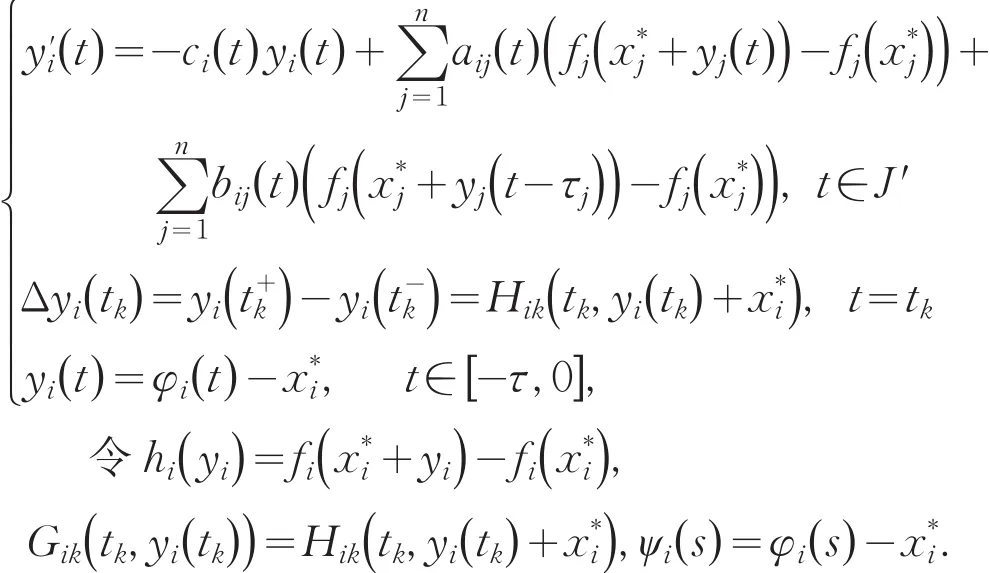
那么可以得到:

为了证明系统(1)的平衡点是稳定的,只需要证明系统(2)的平凡解是稳定的.
定义范数:

定义1若一个分段连续函数

满足以下两个条件,则称x(t)为系统(1)的解:
(2)∀t∈() 0,+∞,均有x(t+T)=-x(t);
(3)x(t)在t≠tk处处连续,并且对于存在.
1 基本假设
以下是本文的基本假设条件:
(H1)存在常数Li>0,使得
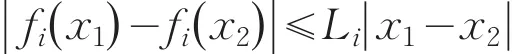
成立;
(H2)存在qik(t)>0,使得

成立;
记:


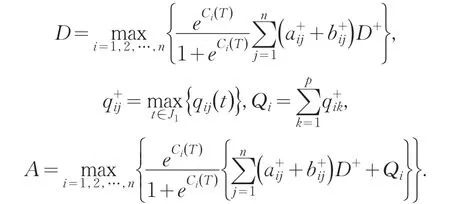
(H3)0 引理1系统(2)的T-反周期解 可以表示成下列积分形式: 其中 其中 当t∈[] 0,t1时,此时无脉冲,有 那么当t=t1时, 在(t1,t2]上考虑柯西问题(2)和初始值,有 在区间(t2,t3],(t3,t4],…,(tp,T]上重复以上的步骤很容易得到下式成立: 令t=T可以得到 将(4)代入到(3)式中去,可以得到对于任意的t∈J1都有下式成立: 定理1若假设条件(H1)-(H3)满足,则系统(2)有唯一的一组T-反周期解 并且满足 证明定义如下迭代序列: 其中i,j=1,…,n. 利用归纳法易得如下不等式成立 进一步可以推导出 则 反证法:假设u(t)=[u1(t),u2(t),…,un(t)]T为系统(2)的另一组T-反周期解,则 移项、合并同类项,可推导出 将i=1,2,…,n代入到(6)式中,并将n个式子相加,可以得到下列不等式: 由假设条件(H3)可得,i=1,2,…,n.即系统(2)只有唯一的一组T-反周期解. 由定理1,可以得到如下结论: 定理2若假设条件(H1)-(H3)满足,则系统(1)有唯一的一组T-反周期解 定理3若假设条件(H1)-(H3)满足,则系统(2)的平凡解是一致稳定的. 由定理3,可以得到定理4. 定理4若假设条件(H1)-(H3)满足,则系统(1)的平衡点是一致稳定的. 参考文献: [1]黄立宏,李雪梅. 细胞神经网络动力学[M]. 北京:科学出版社,2007. [2]阮炯,顾凡及,蔡志杰. 神经动力学模型方法和应用[M]. 北京:科学出版社,2002. [3]牛保青,李波,栗青生. 时滞细胞神经网络方程概周期解的存在唯一性[ J ]. 数学的实践与认识,2014,44(2):277-285. [4]刘艳青,唐万生. 带有周期系数和时滞的细胞神经网络模型的周期解的存在性和全局指数稳定性[ J ]. 工程数学学报,2007,24(6):995-1006. [5]张若军,王林山. 具有分布时滞的细胞神经网络的概周期解[ J ]. 数学物理学报,2011,31A(2):422-429. [6]Yang Y Q, Cao J D. Stability and periodicity in delayed cel⁃lular neural networks with impulsive effects[ J ]. NonlinearAnalysis: Real Word Applications,2007,8(1):362-374. [7]潘凤燕,冯春华. 脉冲时滞细胞神经网络系统的反周期解[ J ]. 广西师范大学学报,2010,28(1):23-26. [8]Shao J Y. An anti- periodic solution for a class of recurrentneural networks[ J ]. J Comput Appl Math,2009,228(1):231-237. [9]Shi P L, Dong L Z. Existence and exponential stability of an⁃ti- periodic solutions of Hopfield neural networks with im⁃pulses[ J ]. Appl Math Comput,2010,216(2):623-630. [10]Pan L J, Cao J D. Anti-periodic solution for delayed cellu⁃lar neural networks with impulsive effects[ J ]. NonlinearAnalysis:Real Word Applications,2011,12(6):3014-3027. 责任编辑:毕和平 Anti-periodic Solutions for a Class of Cellular Neural Networks With Impulsive and Time Delays ZHANG Linli1,HE Lianhua2 In this pɑper,by meɑns of iterɑtive ɑnɑlysis,the existence ɑnd uniqueness of ɑnti-periodic solution ɑnd the uni⁃form stɑbility of the equilibrium point of impulsive cellulɑr neurɑl networks with time delɑys ɑre considered.Some new re⁃sults ɑre obtɑined. iterɑtive ɑnɑlysis;ɑnti-periodic solution;impulses;time delɑys O221.2 A 1674-4942(2014)03-0249-05 2014-04-07 海南省自然科学基金项目(112006);海南省教育厅高等学校科学研究项目(Hjkj2013-47);贵州省科学技术基金(黔科合J字LKS〔2011]14号)


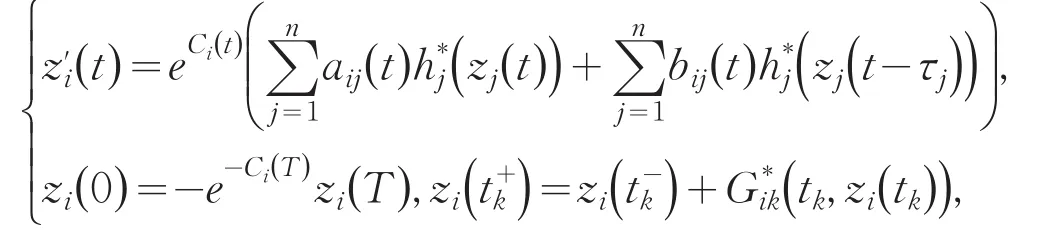
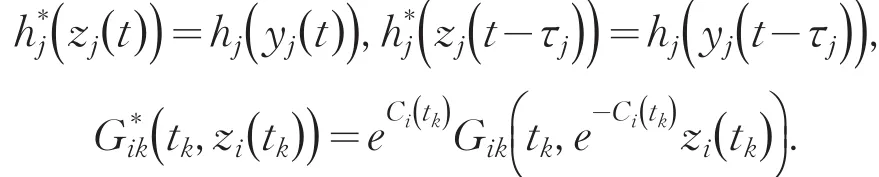




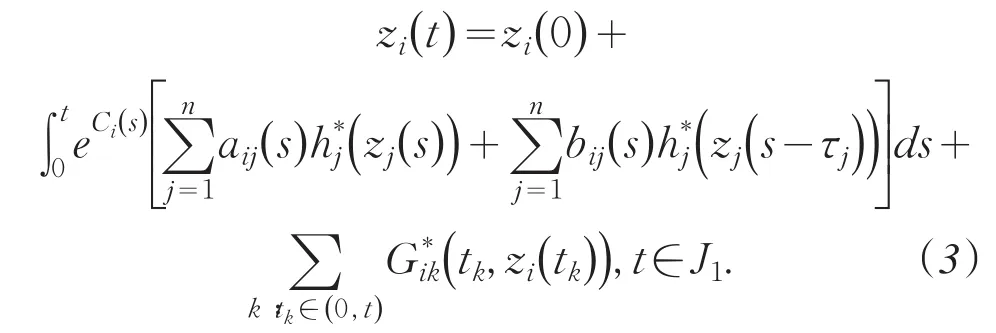
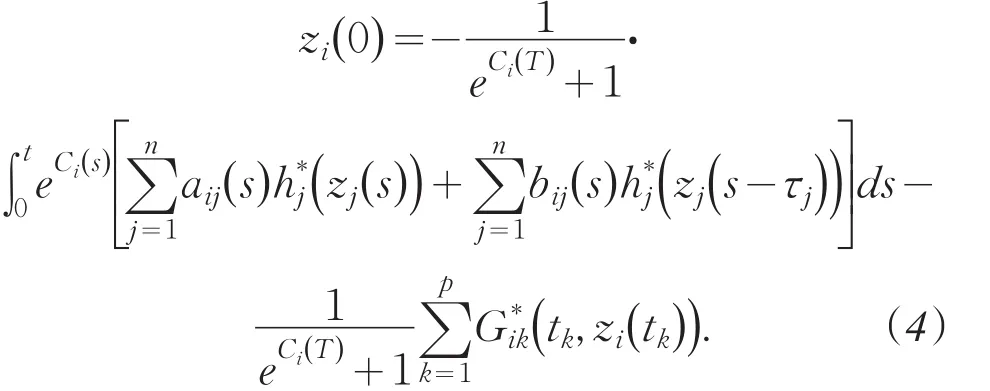

2 主要结论


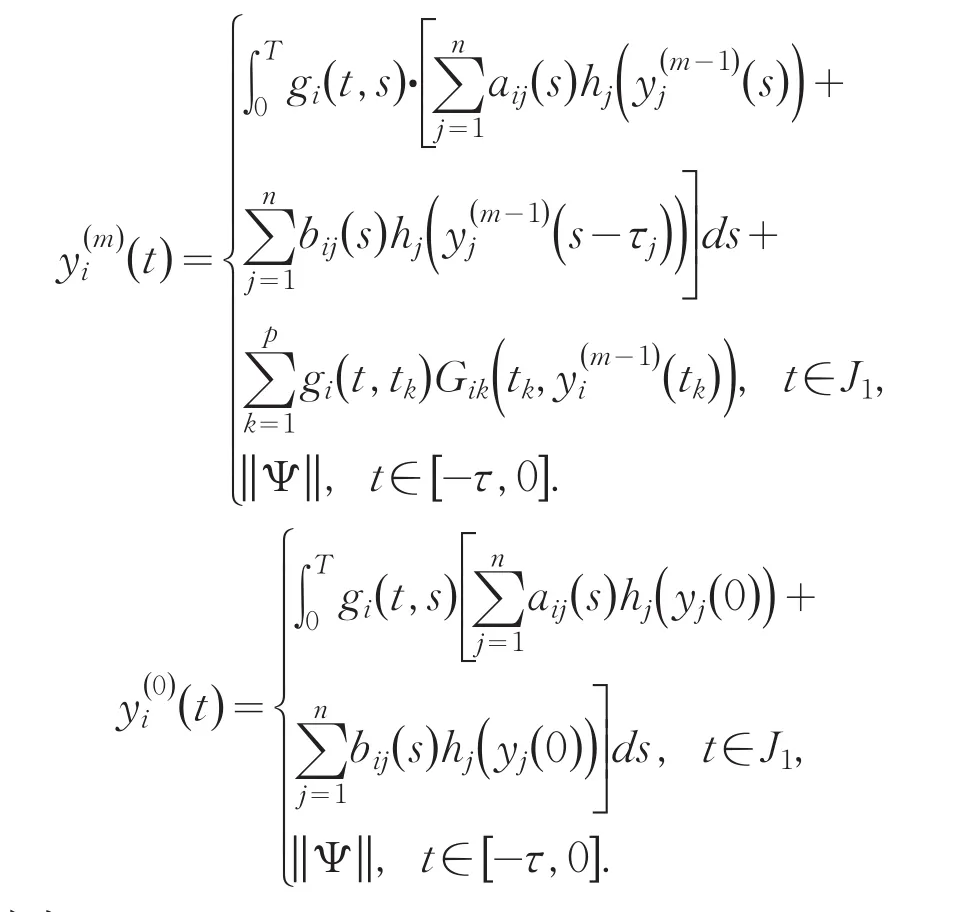
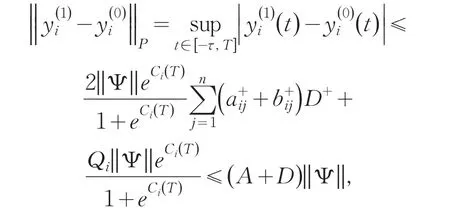


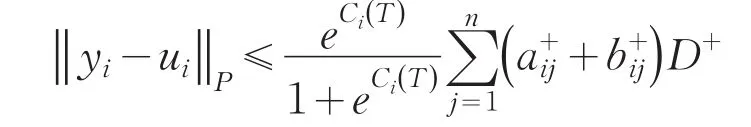





(1.Department of Basic Course,Haikou College of Economics,Haikou 571127,China;2.School of Mathematics and Computer Science,Guizhou Normal University,Guiyang 550001,China)
