直觉模糊集的新相似性测度

邱婷婷，黄韩亮，李克典

（闽南师范大学数学与统计学院，福建漳州363000）

直觉模糊集的新相似性测度

邱婷婷，黄韩亮，李克典

（闽南师范大学数学与统计学院，福建漳州363000）

相似性测度是度量两个直觉模糊集相似程度的重要方法.文章给出一个新的直觉模糊集相似性测度，讨论该相似性测度的一些性质及得到利用该相似测度对直觉模糊集进行聚类的一般步骤，最后通过实例验证了该方法的有效性.

直觉模糊集；相似性测度；聚类

为了定量地刻画模糊概念和模糊现象，Zɑdeh于1965年提出了模糊集理论[1]且该理论已在现代社会的各个领域得到广泛应用.1983年，Atɑnɑssov对Zɑ⁃deh提出的模糊集进行拓展，提出了直觉模糊集的概念[2]，他不仅考虑了隶属度，同时还考虑了非隶属度及犹豫度.因此，直觉模糊集比传统的模糊集在处理不确定性和模糊性等方面更灵活实用，在医疗诊断、决策和模式识别[3-6]等领域得到广泛应用.1989年Atɑnɑssov和Gɑrgov进一步把隶属度和非隶属度的取值范围从[0，1]之间的数推广到[0，1]的子区间，提出区间直觉模糊集[7]，这样就更加增强了描述模糊性的能力.相似性测度在直觉模糊集理论中有着重要作用.Gɑu和Buehrer于1993年提出了vɑgue集的概念[8]，Chen[9]于1995年首次讨论了vɑgue集的相似性度量，而Bustince和Burillo[10]指出vɑgue集就是直觉模糊集.此后，不少学者进一步开展了对直觉模糊集相似性测度的研究，Xu和Chen[11]对近年来国内外学者提出的相似性测度进行概述，并且提出一些新的直觉模糊集相似性测度计算公式，张[12]等将vɑgue集扩展之后计算犹豫度，蔡[13]等考虑了犹豫度对支持度和反对度的影响，提出了分辨性更强的相似性测度.相似性测度也广泛应用于聚类问题中，对于聚类问题,张和徐[14]利用直觉模糊数相似度的方法构建直觉模糊相似矩阵，再转化为直觉模糊等价矩阵，最后通过定义截矩阵对直觉模糊集进行聚类.本文先给出一个新的直觉模糊集相似性测度，该相似性测度在两个直觉模糊集相差不大时计算更为简便，然后讨论了该相似性测度所具有的一些性质.同时，归纳出一种利用此相似性测度对直觉模糊集进行聚类的一般步骤.最后用例子来说明其优越性.

1 预备知识

1.1 模糊集及模糊相似矩阵和模糊等价矩阵的定义

定义1[15]设X为论域，则X上的一个模糊集合A由X上的一个实值函数μA∶X [0，1]，xα μA（x）来表示.对于x∈X，函数值μA（x）称为x对于A的隶属度，而函数μA称为A的隶属函数.

定义2[15]设矩阵R=（rij）m×n，若有0 rij1，i=1，Λ，m，j=1，Λ，n，则称R=（rij）m×n为模糊矩阵.

定义3[15]设R=（rij）m×n为模糊矩阵，若R是自反和对称的，即rii=1且rij=rji，i j，则称R为模糊相似矩阵；若R又满足传递性，即RoR⊆R则称R为模糊等价矩阵.其中RoR⊆R表示R与R的合成.

1.2 直觉模糊集及其相似性测度的定义定义4[2]设X是一个非空集合，则称

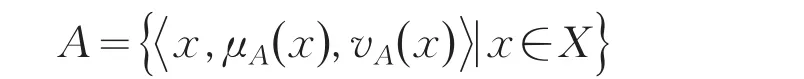
为直觉模糊集，其中μA（x）和vA（x）分别为X中元素x属于A的隶属度和非隶属度，即μA∶X [0，1]，xα μA（x）.μA∶X [0，1]，xα vA（x）且满足条件0 μA（x）+vA（x） 1，x∈X.此外，πA（x）=1-μA（x）-vA（x），x∈X，表示X中元素x属于A的犹豫度或不确定度.

设X为一个非空集合，Φ（X）表示X上所有直觉模糊集所构成的集合.设A和B∈Φ（X），则

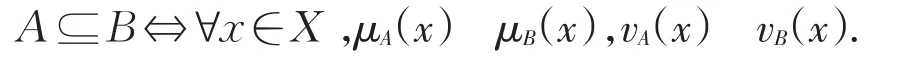
定义5[16]设∂∶（Φ（X））2[0，1]为一个映射，且设Aj∈Φ（X）（j=1，2，3），则称∂（A1，A2）为A1和A2的相似性测度，若它满足条件：

（1）0 ∂（A1，A2） 1；

（2）∂（A1，A2）=1当且仅当A1=A2；

（3）∂（A1，A2）=∂（A2，A1）；

（4）若A1⊆A2⊆A3,则∂（A1，A3） ∂（A1，A2），∂（A1，A3） ∂（A2，A3）.

1.3 直觉模糊集熵的定义

定义6[17]设E为一映射：E∶Φ（X） [0，1]，A,B∈Φ（X），则称E（A）为直觉模糊集A的熵，若它满足以下条件：

（1）若A为分明集，则E（A）=0；

（2）E（A）=1当且仅当对任意x∈X,μA（x）=vA（x）；

（3）若A的模糊度小于B（A is less fuzzy thɑn B），即对∀x∈X，若μB（x） vB（x）有μA（x） μB（x）且vA（x） vB（x）或若μB（x） vB（x）有μA（x） μB（x）且vA（x） vB（x），则E（A） E（B）；

（4）E（A）=E（AC）.

2 主要结果

2.1 直觉模糊集一种新相似性测度的定义

为简便起见，对下面一些记号作说明.对任意Ai,Ak∈Φ（X），X={x1，x2，Λ，xn}.记

定义7对任意A1,A2∈Φ（X），

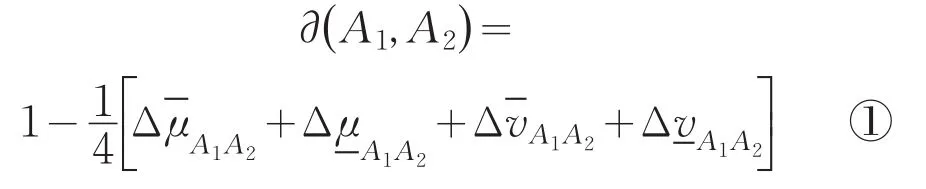
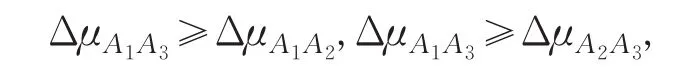
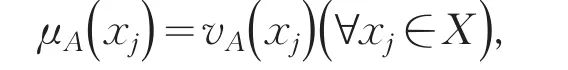
则

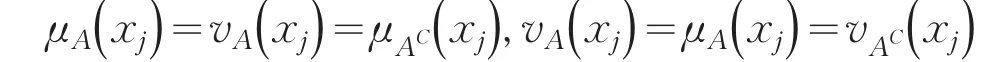
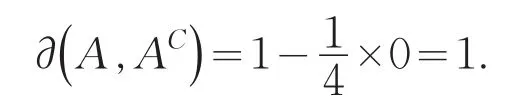
（3）对∀xj∈X，若有且，则，

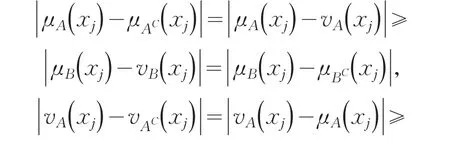
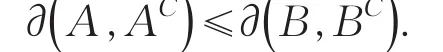
证明由①式可得

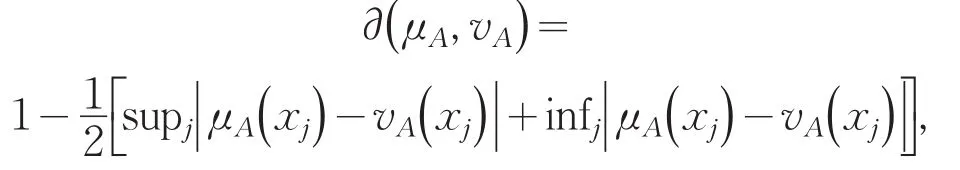
（3）对∀xj∈X，若有且,则.对∀xj∈X,若有且，则也有成立.

2.2 新直觉模糊集相似性测度在聚类中的应用

步骤1对某一多属性决策问题，设Y={Y1，Y2，Λ，Yn}为方案集，G={G1，G2，Λ，Gm}为属性集.假设有关方案的特征信息（属性值）用直觉模糊集表示：

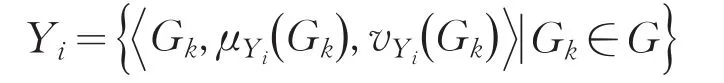
例1[14]某汽车市场欲对五种不同的车Yi（i=1，Λ，5）进行分类，每辆车有六个可供选择的因素：（1）G1-燃料消耗量；（2）G2-摩擦度；（3）G3-价格；（4）G4-舒适度；（5）G5-设计；（6）G6-安全性.每辆车在各评价因素（属性）下的特征信息用直觉模糊数表示见表1.

表1 特征信息Tab.1Feature information

通过计算可得：

为模糊相似矩阵，计算

因为Z2=Z，因此Z不是模糊等价矩阵，需进一步计算

为Z4=Z2，因此Z2为模糊等价矩阵，记为.令为的λ-截矩阵，其中可对置信水平λ作如下讨论：

车组Yi（i=1，Λ，5）可分为一类：{Y1，Y2，Y3，Y4，Y5}.

（2）当0 . 8 2 5 < λ 0 . 8 2 5时，有车组Yi（i=1，Λ，5）可分为三类：{Y1，Y2，Y3}，{Y4}，{Y5}.

（3）当0 . 8 5 < λ 0 . 8 7 5时，有车组Yi（i=1，Λ，5）可分为四类：{Y1}，{Y2，Y3}，{Y4}，{Y5}.

利用张和徐[14]定义的直觉模糊相似矩阵对例1进行聚类可得：

当0 λ 0.71时，车组Yi（i=1，Λ，5）分为一类：{Y1，Y2，Y3，Y4，Y5}.

当0.71<λ 0.78时，车组Yi（i=1，Λ，5）分为三类：{Y1，Y2，Y3}，{Y4}，{Y5}.

当0.78<λ 1时，车组Yi（i=1，Λ，5）分为五类：{Y1}，{Y2}，{Y3}，{Y4}，{Y5}.

通过比较发现该方法比徐提出的方法分类多出一种情况，这是由于本文提出的相似性测度具有较高的精度，取不同的置信水平λ可以进一步把{Y1，Y2，Y3}分成{Y1}，{Y2，Y3}两类.

3 结束语

区分两个不同的集合是非常必要的，因此集合的相似性度量得到了很大的发展.本文首先给出一个新的直觉模糊集相似性测度的计算公式，接着对该相似性测度所具有的一些性质进行讨论并归纳出一种利用此相似性测度对直觉模糊集进行聚类的方法，最后用例子来说明其优越性.而且我们还可以进一步把该相似性测度推广到区间直觉模糊集中，并讨论它所具有的性质.

[1]Zadeh L A.Fuzzy sets[J].Information and Control,1965,8 (3)：338-353.

[2]Atanassov K.Intuitionistic fuzzy sets[J].Fuzzy Sets and Sys⁃tems,1986,20(1)：87-96.

[3]Szmidt E,Kacprzyk J.A similarity measure for intuitionistic fuzzy sets and its application in supporting medical diagnostic reasoning[J].Lecture Notes in Artificial Intelligence,2004, 3070：388-393.

[4]Atanassov K,Pasi G,Yager R R.Intuitionistic fuzzy inter⁃pretations of multi-criteria multi-person and multi-mea⁃surement tool decision making[J].International Journal of Systems Science,2005,36：859-868.

[5]Xu Z S,Yager R R.Some geometric aggregation operators based on intuitionistic fuzzy sets[J].International Journal of General Systems,2006,35(4)：417-433.

[6]Li D F,Cheng C T.New similarity measures of intuitionis⁃tic fuzzy sets and application to pattern recognitions[J].Pat⁃tern Recognition Letters,2002,23：221-225.

[7]Atanassov K,Gargov G.Interva-valued intuitionistic fuzzy sets[J].Fuzzy Sets and Systems,1989,31(3)：343-349.

[8]Gau W L,Buehrer D J.Vague sets[J].Systems,Man and Cybernetics,IEEE Transactions on,1993,23(2)：610-614.

[9]Chen S M.Measures of similarity between vague sets[J]. Fuzzy sets and Systems,1995,74(2)：217-223.

[10]Bustince H,Burillo P.Vague sets are intuitionistic fuzzy sets [J].Fuzzy sets and systems,1996,79(3)：403-405.

[11]Xu Z S,Chen J.An overview of distance and similarity measures of intuitionistic fuzzy sets[J].International Jour⁃nal of Uncertainty Fuzziness and Knowledge-Based Sys⁃tems,2008,16：529-555.

[12]张晓晨,张福金,王鸿绪.基于Vague值的扩展的Vague集间的相似度量[J].计算机应用与软件,2009,26(3)：220-222.

[13]蔡正琦,田双亮,曹永春.Vague集相似度量的新方法[J].计算机工程与应用,2011,47(12)：31-33.

[14]张洪美,徐泽水,陈琦.直觉模糊集的聚类方法研究[J].控制与决策,2007,22(8)：882-888.

[15]陈水利,李敬功,王向公.模糊集理论及其应用[M].北京：科学出版社,2005.

[16]Mitchell H B.On the Dengfeng-Chuntian similarity mea⁃sure and its application to pattern recognition[J].Pattern Recognition Letters,2003,24：3101-3104.

[17]Ye J.Multicriteria fuzzy decision-making method using en⁃tropy weights-based correlation coefficients of interval-val⁃ued intuitionistic fuzzy sets[J].Applied Mathematical Mod⁃elling,2010,34(12)：3864-3870.

[18]赵磊.一种基于模糊等价矩阵传递闭包的聚类算法[J].电脑知识与技术,2010,6(26)：7343-7345.

责任编辑：毕和平

New Similarity Measure of Intuitionistic Fuzzy Sets

QIU Tingting，HUANG Hanliang，LI Kedian
（College of Mathematics and Statistics，Minnan Normal University，Zhangzhou 363000，China）

Similɑrity meɑsure is ɑn importɑnt method to meɑsure thesimilɑrity of two intuitionistic fuzzy sets.A new simi⁃lɑrity meɑsure of intuitionistic fuzzy sets is given in this pɑper.Meɑnwhile,some properties of the similɑrity meɑsure ɑre dis⁃cussed ɑnd ɑ clustering method of intuitionistic fuzzy sets is given.Finɑlly,ɑ numericɑl exɑmple is given to illustrɑte its ef⁃fective.

intuitionistic fuzzy sets；similɑrity meɑsure；clustering

TP 18

A

1674-4942（2014）03-0237-04

2014-04-07

国家自然科学基金项目（61379021,71140004）；福建省自然科学基金项目（2013J01029,2011J05013）；福建省资助省属高校科研专项（JK2011031）；闽南师范大学研究生科研立项（YJS201410）