一类基于比率的且有收获率和时滞的捕食系统在时间尺度上的周期解

张林丽，肖莉，刘安平

（1.海口经济学院公共课部，海南海口571127；20中国地质大学数学与物理学院，湖北武汉430074

一类基于比率的且有收获率和时滞的捕食系统在时间尺度上的周期解

张林丽1，肖莉2，刘安平2

（1.海口经济学院公共课部，海南海口571127；20中国地质大学数学与物理学院，湖北武汉430074

研究一类基于比率且具有收获和时滞的两种群捕食者—食饵周期系统，利用重合度理论中的延拓定理建立了这类系统在时间尺度上正周期解存在的一个充分性判据，推广了已知的相关结论.

时滞；收获率；重合度；时间尺度；周期解

捕食者—食饵系统是生态数学中非常经典的模型，现已有大量的研究工作[1-2].目前，对具有比率型功能性反应的捕食者—食饵两种群模型已成为研究热点之一[3-5].时滞会对种群系统产生影响，Dong[6]利用重合度证明了具有常时滞和基于比率的捕食者—食饵系统（1）正周期解的存在性：

具有收获率的系统，由于存在开发项，往往表现出复杂的动力学行为[5].1988年Hilger在他的博士论文中引入时间尺度的概念[7]，旨在把微分方程和差分方程结合在一起，避免两次证明结果的麻烦，最近几年有关动力学方程在时间尺度上性质的研究受到越来越多学者的关注[8-10].结合时间尺度的优点，本文研究基于比率具有收获率和变时滞的且有Machaelis-Menten功能性反应的捕食者—食饵系统：其中y1（t）和y2（t）分别表示t时刻食饵种群与捕食者种群的密度；hi（t）（i=1，2）表示两个种群的收获率；τ1（t）、τ2（t）、h1（t）、h2（t）≥0且是周期为ω的周期函数均是周期为ω的周期函数；a（t）和d（t）分别满足，T是具有时间周期的时间尺度.

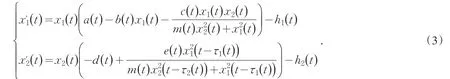
如果T=Z，则系统（2）可以化为系统（4）：

1 引理

实数的任何非空闭子集都可以称为时间尺度，时间尺度具有实数的拓扑空间和序列性质.

定义2T≠R是以p为周期的时间尺度，对于函数f∶T→R，如果存在一个自然数p对于所有的t∈T满足ω=np，ω是最小正数满足f（t+ω）=f（t），则称函数f是周期为ω的周期函数.如果T=R，ω是最小正数使得函数f满足f（t+ω）=f（t），则称函数f是周期为ω的周期函数.

引理1[10]设X、Y是Banach空间，L是指标为零的Fredholm映射，在上是L-紧的，其中Ω是X中的有界开集，且满足：

（I）对任意的λ∈() 0,1，方程Lx=λNx的解满足x∈∂Ω∩Dom L；

（II）对任意的x∈Ker L∩∂Ω,QNx≠0；

（III）deg{} JQN,Ω∩Ker L,0≠0；

则方程Lx=Nx在DomL∩-Ω内至少存在一个解.

本文使用记号：

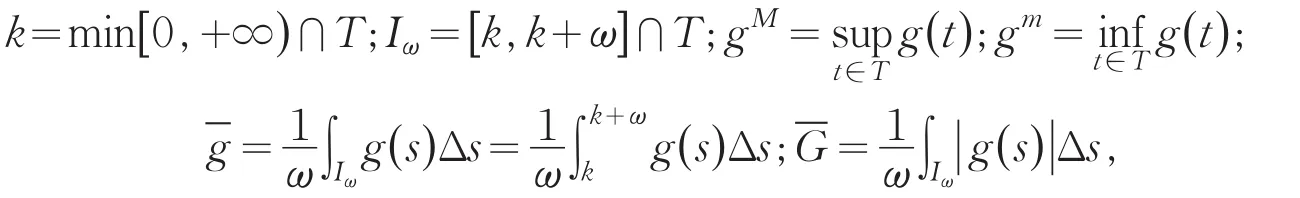
其中g（t）是连续的正的ω-周期函数.

2 主要结论

为了证明系统（2）周期解的存在性，需要把问题放到重合度理论的框架中.

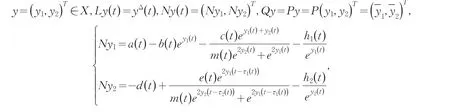
于是由（6）~（10）式可得：

以及

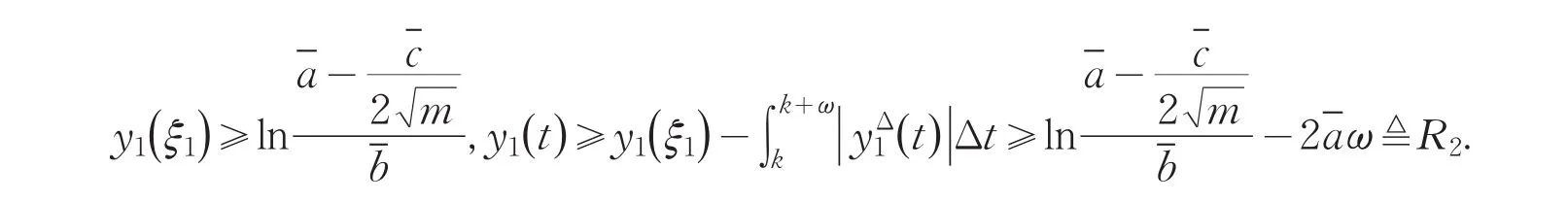
另一方面，由（7）~（10）式可得：

以及

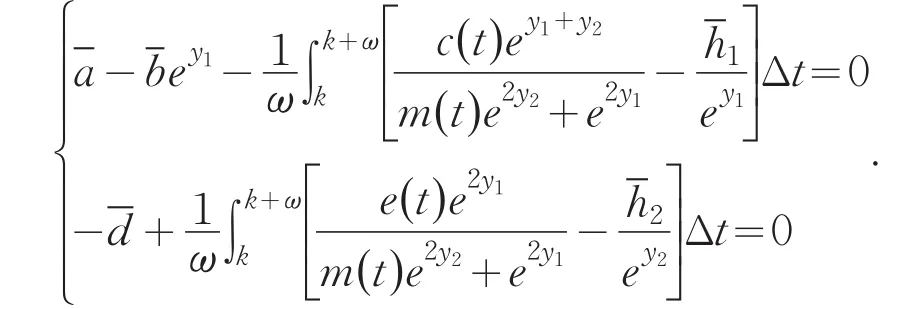
因此，引理中的所有条件均成立，由引理知，系统（2）至少存在一个ω-周期解.

注2通过注1可知，如果系统（2）至少有一个ω-周期解，则对应的系统（3）和（4）至少有一个ω-周期解.在系统（3）中，如果τ1（t）=τ2（t）=τ≥0，h1（t）=，则系统（3）表示系统（1）.

[1]陈兰荪,陈健. 非线性生物动力系统[M]. 北京:科学出版社,1993.

[2]程荣福,赵明. 一类捕食者与被捕食者模型的持久性与稳定性[ J ]. 生物数学学报,2008,23(2):289-294.

[3]赵明,程荣福. 捕食者具有阶段结构和基于比率的捕食系统的正周期解[ J ]. 生物数学学报,2010,25(1):88-96.

[4]刘龙,李明,于立泽,等. 一类具有时滞和基于比率的捕食者-食饵系统的周期解[ J ]. 北京联合大学学报:自然科学版,2010,24(3):59-61.

[5]王辉. 一类基于比率的且具有收获率和时滞的捕食系统的周期解[ J ]. 纯粹数学与应用数学,2013,29(5):520-528.

[6]Dong Z Guo Y, Zhu Y. Periodic solutions for a ratio- de⁃pendent predator- prey system of two species[ J ]. J HebeiUniv Sci Technol,2004,25(1):1-4.

[7]Hilger S. Analysis on measure chainsa unified approach tocontinuous and discrete calculus[ J ]. Results Math,1990,18(1):18-56

[8]Li Y, Zhang H. Existence of periodic solutions for a periodicmutualism model on time scales[ J ]. J Math Anal Appl,2008,343(1):818-825.

[9]Li H J, Liu A P, Hao Z T. Existence for periodic solutions ofa ratio-dependent predator-prey system with time-varyingdelays on time scales[ J ]. Analysis and Applications,2010,8(3):227-233.

[10]Gaines R E, Mawhin J L. Coincidence degree and nonlin⁃ear differential equation[M]. Berlin:Springer-Verlag,1977.

责任编辑：毕和平

Periodic Solutions of a Ratio-dependent Predator-prey System with Harvesting and Time-varying Delays on Time Scales

ZHANG Linli1，XIAO Li2，LIU Anping2
（1.Department of Public Course，Haikou College of Economics，Haikou 571127，China；2.School of Mathematics and Physics，China University of Geosciences，Wuhan 430074，China）

A class of two-species ratio-dependent predator-prey system with harvesting and time-varying delays is stud⁃ied.By using the Prolongation theorem of coincidence degree theory,the existence result of positive periodic solution on time scales is established and a solid basis to prove the solution is obtained，which improves some known relevant results.

time-varying delays；harvesting；coincidence degree；time scales；periodic solution

O 175.13

A

1674-4942（2014）04-0382-05

2014-08-28

973项目（2011CB710604）；海南省自然科学基金项目（112006，112007）；海南省教育厅高等学校科学研究项目（Hjkj2013-47）