换流站阀厅结构的非线性动力分析

胡孝平，袁 健

（1.苏州市吴江区代建项目管理局 ，江苏苏州215000；

2.中南林业科技大学土木工程与力学学院，湖南长沙410004）

换流站阀厅结构的非线性动力分析

胡孝平1，袁 健2

（1.苏州市吴江区代建项目管理局 ，江苏苏州215000；

2.中南林业科技大学土木工程与力学学院，湖南长沙410004）

采用有限元软件SAP2000对一钢框架－剪力墙结构的换流站阀厅在罕遇地震作用下的非线性动力性能进行分析。计算过程中，分别使用了三条典型地震波，最后分别得到了柱顶位移、柱底力及索轴力的时程曲线。计算结果表明，在罕遇地震作用下，结构位移可满足规范的要求，但索轴力和柱底力的增幅均较大，在设计时应给予重视。

SAP2000；阀厅；罕遇地震；动力分析

随着我国电网的高速发展，换流站在全国得到了广泛的应用。换流站阀厅结构不仅是直流输电工程建设中的关键性设施之一，而且也是电网系统工程中不可或缺的一个组成部分，其主要结构特点是在屋架下悬吊有多组大质量的阀组，抗震规范对于具有悬吊质量结构没有给出其在地震作用下结构计算的取值方法。换流阀组和悬索是换流站中的关键设备，它们的工作条件对抗震也有严格要求，因此阀厅结构抗震性能的研究日益受到重视［1－5］。

对于具有悬吊质量的结构体系，国内外均已进行过专门的研究，但研究的重点主要是结构的振动控制，且多数也是为了减震才加入悬吊质量的，因此，在计算中往往忽略悬吊质量摆动产生的离心力及其对结构产生的效应。阀厅结构的悬吊阀组是作为其固有的组成部分而存在的，由于阀组的质量很大，因此为了保证阀厅设备的安全运行，有必要对其悬吊阀组在罕遇地震作用下的索轴力及相应的结构效应进行研究。

1 结构体系及有限元模型

该结构采用钢框架－混凝土剪力墙的混合结构形式，并且还具有多组大质量的悬吊阀组。此阀厅结构阀组设备在吊梁处的平面布置如图1所示，⑦轴处的剖面如图2所示。Ⓕ轴采用钢筋混凝土剪力墙，由于其还有特殊的工艺要求，一般称作防火墙。①轴、Ⓐ轴及屋架采用钢结构 ，钢柱的截面为HW600×600×18×25。阀组及其相关设备采用悬索悬挂于水平钢梁上，阀组共有6层，层与层之间采用悬索连接，整个结构共有6组阀组，一组阀组重12 t，屋面活荷载［6］取0.5 kN／m2。

图1 阀厅结构平面布置

图2 阀厅结构剖面示意

该阀厅结构位于7度地震区，房屋总长度52m，总宽度21.87m，建筑物总高度20.6m。

采用SAP2000进行非线性动力分析，防火墙采用分层壳单元模拟，材料包括钢筋和混凝土，其中钢筋层可以根据已有钢筋面积换算成钢筋层。分层壳单元考虑了面内弯曲－面内剪切－面外弯曲之间的耦合作用，剪力墙的塑性行为是通过对分层壳模型的非线性分析来实现的。

钢屋架及钢柱采用梁单元模拟；悬吊阀组采用壳单元模拟；阀组的悬索采用索单元模拟，只受拉不受压，SAP2000中对此单元的处理是非线性的；所有材料的强度均取标准值；分析中主要考虑结构几何非线性、索及钢柱塑性铰的非线性。阀厅结构的有限元模型如图3所示。

1.1 塑性铰

目前国内规范尚未提供构件弹塑性变形限值，国际上一般采用以抗震性能为基准的FEMA356［7］所提供的限值。

弯矩－转角的非线性恢复力滞回曲线的骨架曲线根据FEMA356建立，如图4所示。在A点与B点内，铰内没有变形发生，所有弹性变形在框架单元内发生，点 IO，LS及CP代表能力水平，它们分别对应直接使用、生命安全及防止倒塌。

图3 阀厅结构的有限元模型

图4 弯矩－转角关系曲线

在①至⑧轴柱底分别定义PM铰，塑性铰的属性基于FEMA356，其属性还依赖于截面。

在SAP2000中规定，铰的行为是刚塑性的，没有弹性行为的；当框架单元出现塑性行为时，塑性行为全部在铰内部发生，而框架只发生弹性变形。

1.2 动力方程的数值解法

采用逐步积分的Wilson－θ法，这是一种无条件稳定的线性加速度方法［8－9］。在罕遇地震作用下结构的阻尼比取5%。

运用Wilson－θ法，可对水平地震作用下的阀厅结构进行非线性动力分析，求解结构的运动方程，从而得到结构在计算时间内每一时刻的地震反应。

2 模态分析

屋面的维护结构和墙面均选用压型钢板，荷载的取值在有限元计算时仅考虑其自重，最后将各钢板的自重及屋面的活荷载均转化为线荷载作用在结构上而不考虑压型钢板对结构的支撑作用［5］。

结构模态分析的主要误差在于结构质量的统计上，在SAP2000中结构的质量和自重是两个相互独立的概念，可以采用质量源的概念来得到用于结构模态分析的结构质量。由钢板自重转化而来的线荷载可再一次转化为质量源参与结构的模态分析。表1给出了结构振型对应的周期［10－12］。

s

表1 阀厅结构的自振周期 单位：

表1为阀厅结构前5阶自振周期，由表1可以看出，是否挂阀对结构自振周期影响很小，挂阀前与挂阀后的振动模态是相似的，其中表1所列模态为整体结构的振动模态（不包括阀体的振动模态），其中第一振型为纵向平动，第二振型为横向振动，第三振型为扭转振动，且扭转主要表现在①号轴这一侧，由于⑨至⑩轴处存在多片剪力墙，因此刚度较大，在第三阶模态中表现不明显。由上述模态分析结果可见，本文与文献［13］的分析结果相比明显不同，主要是因为本文所采用的防火墙为钢筋混凝土剪力墙且总体结构形式较文献［13］不规则，而文献［13］中的防火墙采用的是框架且总体结构形式较为规则，因此模态分析结果表现出一定的差异性。

3 不同地震波作用下结构的响应

震害结果表明，结构承载力是正常使用的保证，结构的耗能和延性是大震不倒的保证。因此在进行结构设计时，不仅要对结构进行小震作用下的计算，还需对其进行大震作用下的变形验算。由于该阀厅结构同一般工业厂房没有太大的差别，在静力计算与设计等各方面都比较成熟，因此本文着重探讨阀组悬索在地震作用下的内力变化及其对结构抗震性能的影响，为该类结构的设计提供参考［5，14－16］。

计算时采用三条波分别为El－Centro波，记录时间（1940年5月18日），卓越周期为0.55 s、Taft波，记录时间（1952年7月21日），卓越周期为0.44 s及天津波，记录时间（1976年11月25日），卓越周期为0.9 s。与基本烈度7度对应的罕遇地震作用下的水平地震加速度峰值为220 gal，因此笔者将各地震波的峰值加速度均调整为220 gal。在进行动力非线性分析时，选择Sap2000中的直接积分的非线性时程分析。结构③号轴线对应钢柱的力、位移时程曲线，如图5所示；结构一组索（六根索）的轴力时程曲线，如图6所示，其中索轴力为悬吊阀组在摆动过程中产生的动拉力，不包括阀组本身的自重；图中所示柱的力、位移时程均为动力反应部分（不含静力分析部分）。各钢柱顶的静动力位移峰值如表2所示。

动力计算的结果表明，各钢柱的底部均未出现塑性铰，钢柱底部仍处于弹性工作状态。由图5及表2，表3可知，在罕遇地震作用下，结构的响应较大，但以钢柱处的最大位移计算的层间位移角不到2／1000。柱底轴力最大增幅达20% ，柱底剪力最大增幅达10%，其最大剪应力水平仍远小于1，不会出现剪切破坏，柱底弯矩最大增幅达49%；由图6可知，其中索的轴力最大增幅达18%。构件内力的最大增量取［Max（地震作用下的内力）／静力分析的内力］－1。由于阀组在振动的过程中会产生比较大的离心力，因此柱底轴力的增加幅度受此因素的影响较大，索轴力与柱底轴力的增大幅度表现比较接近［5］。

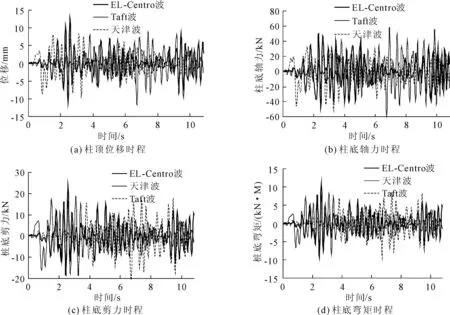
图5 钢柱的力、位移时程

图6 索轴力时程

表2 柱顶位移 单位：mm

表3 结构地震反应部分峰值比较

由表3可知，在罕遇地震作用下，阀厅结构柱顶的动位移峰值为12.8mm（El－Centro波），柱顶位移的最大反应相差可达38%，因此不同场地类别的地震波对结构柱顶位移反应的影响较大。

4 结 论

由于阀厅结构的功能要求，在其剪力墙一侧共布置了七片横向防火墙，使得整个结构的横向刚度得到了增强，所以结构的纵向振动模态早于横向振动模态的出现。结构的振动主要包括悬吊阀组各质量块的来回摆动及扭转与整体结构的平动、扭转及部分杆件的局部振动。

换流站阀厅结构非线性地震反应分析的计算结果表明：

（1）在7度罕遇地震作用下，结构的响应较大，结构柱顶位移可满足规范的要求。在阀厅结构抗震研究中，最关键的设备是悬索与阀组，其中索的轴力最大增幅达18%，由于现在还缺少相关试验数据，其安全性有待试验验证；柱底轴力、剪力及弯矩最大增幅分别达20%、10%及49%。由于阀组的振动对柱底轴力的增加幅度产生了较大影响，因此索轴力与柱底轴力的增大幅度表现比较接近。其中，柱底弯矩增幅最大，需引起重视，但由于此处设计的柱子断面尺寸较大，其一直未进入塑性工作状态，设计偏于保守。

（2）由于结构动力特性的复杂性，柱顶位移反应受不同场地类别地震波的影响较大。

［1］ 赵成刚，冯启民.生命线地震工程［M］.北京：地震出版社，1994.

［2］ 柳春光，林 皋，李宏男，等.生命线地震工程导论［M］.大连：大连理工大学出版社，2005.

［3］ 胡聿贤.地震工程学［M］.北京：地震出版社，2006.

［4］ 魏文晖，周兴乐 ，胡孝平 .换流站阀厅结构的地震效应动力分析［J］.建筑结构，2010，40（3）：75－77.

［5］ 胡孝平.悬吊质量结构的动力分析［D］.武汉：武汉理工大学，2008.

［6］ 中华人民共和国住房和城乡建设部，中华人民共和国国家质量监督检验检疫总局.GB 50009－2012.建筑结构荷载规范［S］.北京：中国建筑工业出版社，2012.

［7］ Federal EmergencyManagement Agencyfema.356 Prestandard and commentary for the seismic rehabitlitation ofbuilding［S］.Washington：The Building Seismic Safety Council，2000.

［8］ 李桂青.抗震结构计算理论和方法［M］.北京：地震出版社 ，1985.

［9］ 吴晓枫，余 萍 ，胡孝平 .某框架结构加层后的地震反应控制分析［J］.水利与建筑工程学报 ，2008，6（3）：44－46.

［10］ 北京金土木软件技术有限公司.SAP2000中文版使用指南［M］.北京：人民交通出版社，2006.

［11］ 傅志方.振动模态分析与参数识别［M］.北京：机械工业出版社，1990.

［12］ Ward H，Stefan L，Paul S.Modal Analysis Theory and Testing［M］.Katholieke Universiteit Levven Department WerktviGkunde，1997.

［13］ 刘宗辉，吴 轶，蔡 健，等.带悬吊阀体的大型换流站阀厅结构地震反应分析［J］.建筑结构 ，2012，42（10）：119－123.

［14］ Nikolaenko N A，Burgman IN.Earthquake Resistance of Structures With Suspended Masses［C］.Ashrae Transactions，1976.

［15］ 王前信，卢书辉.悬吊体系的地震力［M］.北京：地震出版社，1981.

［16］ 王玉朋，魏 琏.悬吊质量结构的抗震计算方法［J］.工程抗震与加固改造，1989，12（2）：1－11.

Non－linear Dynamic Analysis of the Valve－hall Structure

HU Xiao－ping1，YUAN Jian2
（1.Administration of Agent Construction Project，Wujiang Districtof Suzhou City，Suzhou，Jiangsu 215000，China；2.School of Civil Engineering and Mechanics，Central South University of Forestry&Technology，Changsha，Hunan 410004，China）

The non－linear time－history analysis of steel frame－shearwall structure of the valve－hallwas presented，three typical seismicwaveswere used and the analysis of the valve－hallwas accomplished by using the finite element software SAP2000.Finally，the time－history of top of the column displacement，bottom of the column force and axial force of the cableswere obtained.The results indicate that the seismic performance of the valve－hall can satisfy the criterion of the seismic code in rare earthquakes But the bottom of the column force and axial force of the cableswere highly increased in the analysis，somore attention should be given to the design regarding to this.

SAP2000；valve hall；rare earthquake；dynamic analysis

TU398＋.2

A

1672—1144（2014）04—0120—04

10.3969／j.issn.1672－1144.2014.04.023

2014－02－18

2014－03－13

住房和城乡建设部科技研发项目（2013－K4－21）

胡孝平（1982—），男 ，江苏苏州人 ，硕士 ，工程师，主要从事建筑结构的抗震设计与理论研究。