偏微分方程性质对大坝安全监控的意义

方卫华

（1.南京理工大学理学院，江苏南京210094；2.水利部南京水利水文自动化研究所，江苏南京210012）

偏微分方程性质对大坝安全监控的意义

方卫华1，2

（1.南京理工大学理学院，江苏南京210094；2.水利部南京水利水文自动化研究所，江苏南京210012）

为夯实大坝安全监控理论基础，采用理论分析的方法，以典型二阶线性偏微分方程解的极值原理、解的存在唯一性和稳定性、影响区域以及时间反演对称性等性质为例，给出了偏微分方程性质在大坝安全监控包括测值分析、监控仪器布置、仪器量程选择和误差估计等方面的理论指导作用。分析结果表明熟悉偏微分方程的性质对提高大坝安全监控理论水平具有重要意义。

偏微分方程；大坝安全监控；模型建立；误差估计

大坝安全监控的发展离不开相应的数学和力学理论，如应用应变张量（第一）不变量进行应变计组误差分析、有效应力原理进行埋设渗压计测值分析以及弹性地基梁和悬臂梁解析解确定变形监控统计模型的因子等［1］。众所周知，偏微分方程是描述自然规律的有力工具，在大坝安全监控中，常见的热传导、振动和稳定渗流场（温度场）以及弹性力学等问题都可以分别归结为抛物型、双曲型和椭圆型偏微分方程加以研究［2］。尽管有关偏微分方程研究的成果众多，但直接应用偏微分方程理论指导大坝安全监控的工作还未涉及［3］。也正是因为如此，随着大坝安全监控实测数据的不断增加，人们越来越意识到加强大坝安全监控相关理论研究的重要性，大坝安全监控理论的发展已成为制约大坝安全监测技术进一步发展的瓶颈。实际上，深入理解偏微分方程的数学性质不仅是建立相应测值数学模型、反演相关物理参数的基础，而且对大坝安全监控中的误差分析、测点布置和仪器选型等都具有十分重要的意义。为此，本文将以二阶线性偏微分方程为例，分析其在指导大坝安全监控方面的作用，借此引起人们对理论研究的重视。

1 偏微分方程与大坝安全监控的关系

1.1 大坝安全监控中的常见偏微分方程及分类

（1）不稳定的热传导和渗流问题可以用抛物型方程加以描述，如混凝土大坝施工期湿度和温度传导、多层多孔介质中部分饱和渗流问题描述的具有间断系数都可以用非线性抛物方程描述，如平面正交各向异性不稳定渗流方程可以写成［4－9］：

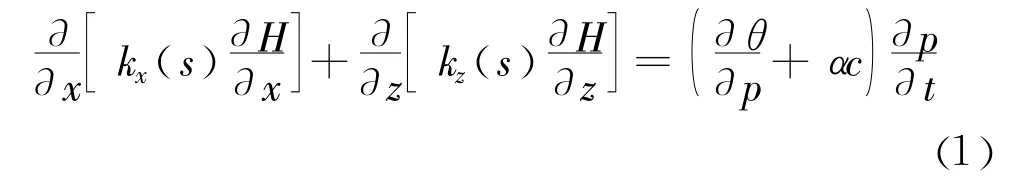
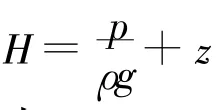
（2）地震、泄洪或发电诱发振动、波浪或水锤冲击等导致的大坝振动和波传播问题都可以用双曲方程加以描述。

（3）在稳定或平衡状态研究中，椭圆型方程在工程安全中占据重要位置，如稳定温度场、稳定渗流场以及弹性力学平衡问题等都可以用椭圆方程加以描述。

对于线弹性体，设其位移场为 u＝ ［u1，u2，u3］T，则用位移分量表示的平衡微分方程为［10］

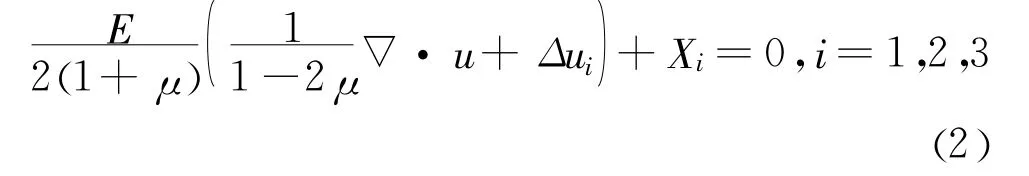
其中：Xi为对应方向的体力分量；E、μ分别为杨氏弹性模量和泊松比。可见式（2）为椭圆型方程。

平面问题两个正交方向的正应力之和（σx＋σy）满足Possion方程，如平面应力条件下，应力满足：

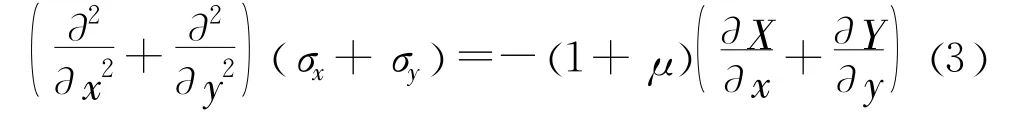
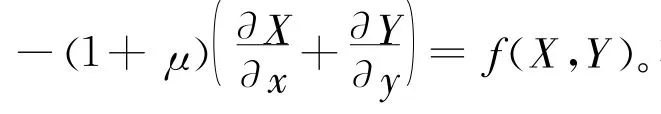
当只受到空间常体力（如重力坝或惯性力）条件下，式（3）和式（4）相应的Possion方程转化成标准Laplace方程Δ（σx＋σy）＝0。可见线弹性力学中许多方程都可以转化为（二阶）椭圆方程（组）。总之，稳定渗流场、温度场和平衡问题都可以归结为椭圆型偏微分方程问题。

1.2 偏微分方程类型转化与大坝安全性态演化的关系

一类偏微分方程对应一类工程安全的状态及其演化，方程的系数反映具体结构参数或各种参数之间的耦合影响。如式（1）中渗透系数是饱合度的函数，在不同的结构状态下，这种函数关系是不同的［11］。方程系数的变化 ，包括系数数量及其物理内涵的变化是工程结构状态发生改变的显著标志。当方程系数变化时，线性偏微分方程可能转化为另外的线性偏微分方程、半线性偏微分方程、拟线性偏微分方程甚至完全非线性偏微分方程。总之，方程类型的改变反映了工程安全状态的改变，而通过方程类型和性质也可以分析大坝的安全状态。

现以涉水（风）工程方面的Navier－Stokes方程（组）为例进行说明。Navier－Stokes方程（组）是分析工程荷载和液固耦合系统稳定的基础。根据不同的简化，Navier－Stokes方程（组）属于不同的类型，如一维非定常Euler方程为双曲型、二维（非）定常Euler方程为双曲型或双曲－椭圆型、定常不可压缩方程为椭圆型、定常可压Navier－Stokes方程是双曲椭圆型、利用边界层理论简化的Navier－Stokes方程为抛物型方程等。可见Navier－Stokes方程（组）的类型依赖于流场的特性，它们可能是椭圆型、抛物线型、双曲线型或混合型［13－14］。

利用实测资料建立偏微分方程尚有一定的难度，利用实测资料和相应偏微分方程的匹配程度确定工程或结构所满足的微分方程，或直接利用数据同化方法，将实测资料和数理方程进行结合，这也是利用偏微分方程分析工程安全状态的有效方法［1］。

2 典型偏微分方程性质及其作用

2.1 极值原理与上下界估计

古典解估计包括解及其梯度估计，前者可以为监测仪器的量程选择和粗差分析提供基础，后者对测点布置疏密起指导作用，即在待监测物理量空间梯度大的地方测点加密，空间梯度比较小的位置降低测点密度。在时间梯度大的地方加密测次，在时间梯度小的地方降低测次［15］。

2.1.1 抛物型方程

在大坝安全监控中的常见二阶抛物型方程的混合初边值问题可以写成：

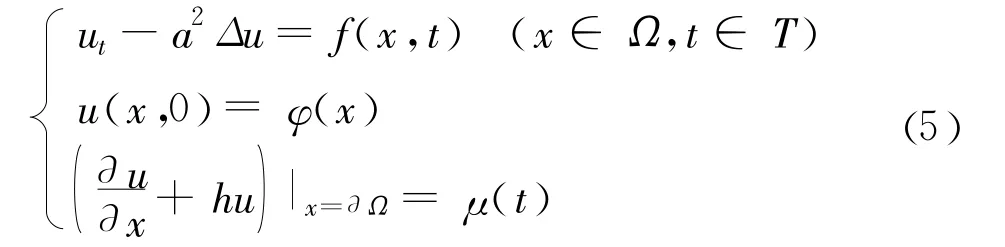
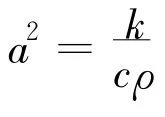
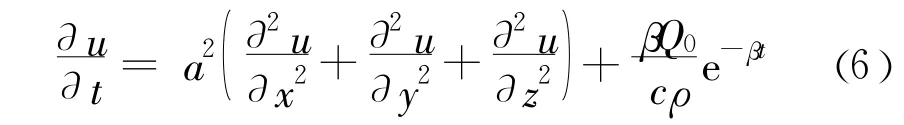
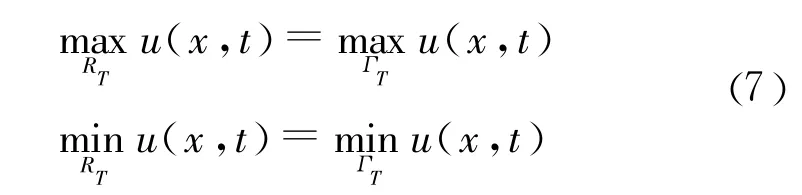
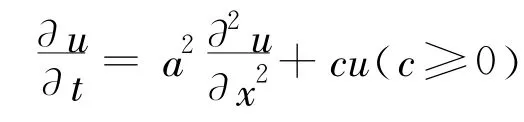
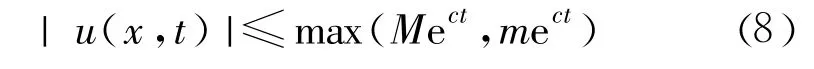
类似地，当温度场或渗流场等监测物理量 u∈C2，1（ΩT）∩ C（）满足如下方程：

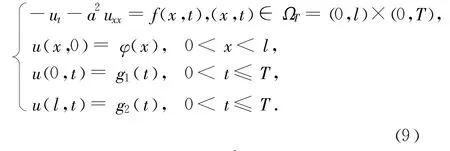
对于区域上初始条件已知，且 u∈C2，1（QT）∩C（）满足如下抛物方程：

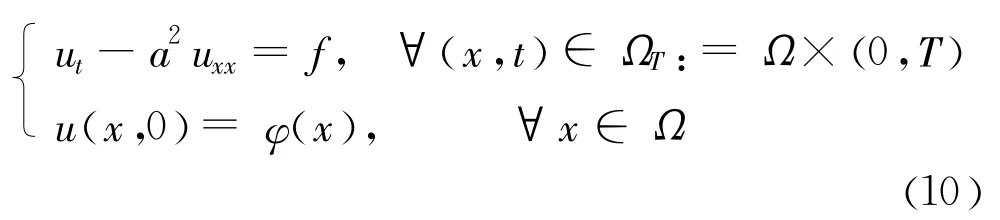
总之，对于一般的抛物型方程，其极值总在抛物边界上达到，而对于式（8）、式（9）和式（10），温度场或渗流场等将满足更严格的有界条件。这对于不稳定温度场或渗流场的测值分析和仪器量程选择等都具有十分重要的指导意义。

2.1.2 双曲型方程

双曲型（波动）方程混合问题可以表示为：

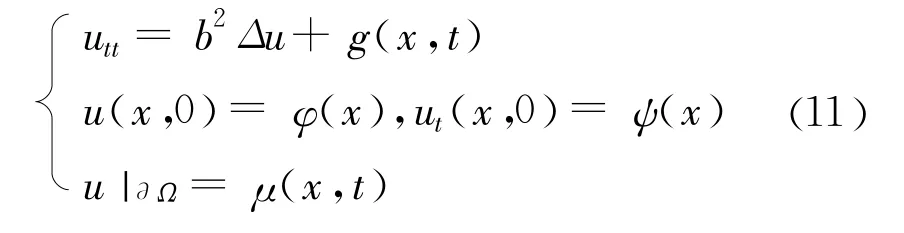
波动方程一般不存在极值原理，即对于振动难以找到振动位移的极大值满足的规律。当初始条件满足不强的约束条件时，对多个空间变量的双曲型方程组的Cauchy问题甚至连整体光滑解都不可能存在［12］。

2.1.3 椭圆型方程

设稳定条件下大坝的温度场、渗流场函数为u（x，t），则函数 u（x，t）为Laplace方程的解。当u（x，t）在¯Ω上连续时，则 u（x，t）一定在边界∂Ω上取到最大值和最小值。即若在边界∂Ω上成立u≤v，则在 Ω内也成立着u≤v。并且只有u≡v时，在Ω内才会有等号成立。根据式（2），在满足平面假设条件下，应力增量的第一不变量在边界取得极值。类似地可以得到椭圆型方程的非负最大值原理和Hopf边界点引理。

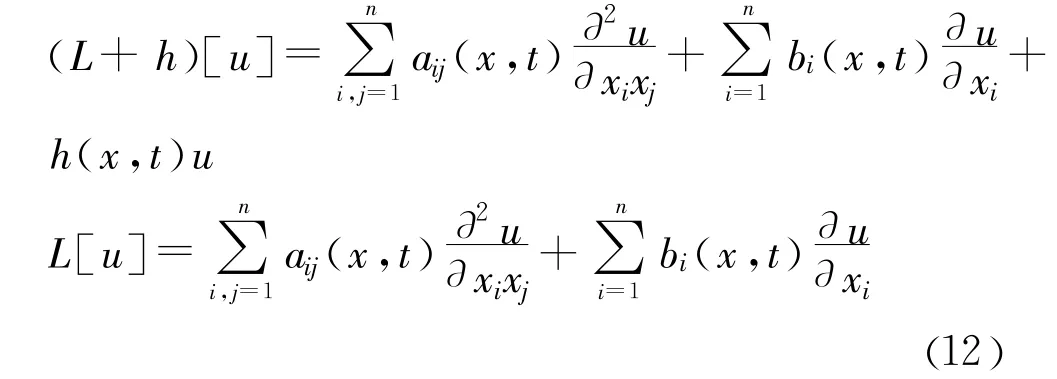
假设 u∈C2（Ω）∩C（¯Ω）为式（12）的任意一个解，且 L满足在 Ω中是一致椭圆型的和（L＋h）［u］＝f（x）≥0，h≤0及L的系数一致有界，则：

（1）u在¯Ω上的非负最大值必在Ω的边界∂Ω上达到，即max｛u（x）|x∈¯Ω｝＝max｛u（x）|x∈∂Ω｝；

（2）若 Ω单连通而且存在一点x0∈ Ω，使得u（x0）＝ max｛u（x）|x ∈ ¯Ω｝，则 u（x0） ≡u（x）｛∀x∈¯Ω｝。

抛物、双曲及椭圆型方程解及其梯度往往对应大坝安全监控中的重要物理量及其分布，一般情况下，对解或其梯度进行估计常运用古典Hopf第一、第二极值原理，在此基础上推导出由这些方程边值问题的解或解的梯度所定义的范函的极值原理［17］。

2.2 唯一性和稳定性

2.2.1 抛物型方程

抛物型方程（4）在区域Ω×T上的解是唯一的，而且连续地依赖于边界∂Ω×0上所给定的初始条件及边界条件。上述定理说明：①在初始条件和边界条件相同的情况下，即 φ（x）、μ（x）、g（x，t）相等时，实测资料在理论上应该是唯一的，如考虑测量系统的误差，每次（多次）测值应该在理论值加一定的允许误差范围内，满足一定的重复性。②当边界条件（或初始条件）分别为 φ1（x）＜ φ2（x）＜ φ3（x）时，对应的实测资料在剔除仪器测值误差后也应该满足 m1（x）＜ m2（x）＜ m3（x）。③由定理2可知，通过长时间的边界测量 g（x，t），可以获得对应的区域 Ω的内部测值u（x，t），即在准确知道材料参数 a的前提下，无需在内部设置测点。

2.2.2 双曲型方程

双曲型（波动）方程（10）的解是唯一的，并且解u连续依赖于初值φ（x），ψ（x）及右端项g（x，t）。其中 u（x，t）为不上述说明波动方程初边值问题的解u（x，t）在下述意义下关于初始值（φ，ψ）与方程右端项f是稳定的，即对任何给定的ε＞0，一定可以找到仅依赖于ε和T的η＞0，只要 ‖φ1－φ2‖≤ η，‖φ1x－φ2x‖L2（Ω）≤ η，‖φ1y－φ2y‖L2（Ω）≤η，‖ψ1－ψ2‖≤ η，‖f1－f2‖≤ η，那么以（φ1，ψ1）为初值、f1为右端项的解 u1与以（φ2，ψ2）为初值、f2为右端项的解u2之差在0≤t≤ T上满足

2.2.3 椭圆型方程

对于有限区域的Dirichlet内问题：

的解存在唯一，且连续依赖于边值条件。

对于地下厂房或洞室等Dirichlet外问题：

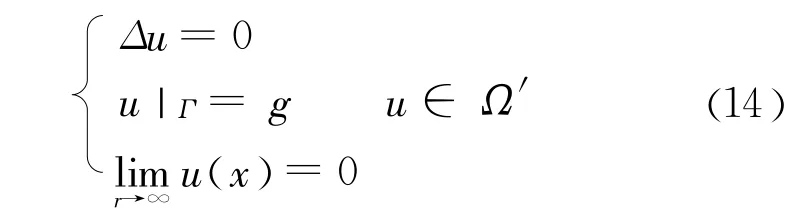
的解存在且唯一，并连续依赖于边值条件。Neumann内问题：

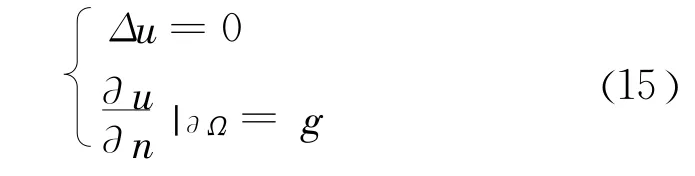
的解存在，则除相差一常数因子外，解是唯一的。Neumann外问题：

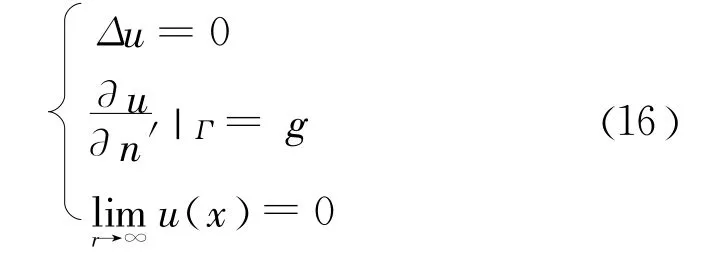
解存在且唯一。总之调和方程第一、第二和第三边值问题的解如存在必唯一。对于 Possion方程和Helmholtz方程和Lame－Navier方程也被证明，如果解存在必唯一。

由上述定理可知，椭圆型方程的解完全依赖于边界条件，因此只需要获得边界条件（根据边界条件确定），即只需要在边界获得荷载和作用信息，以及材料的物理参数，即可获得结构内部场的分布，从而检验实测资料的正确性和进行有关预测。

2.3 影响区域与依赖区域

影响区域与依赖区域是测点布置、反演分析、测值分解、因子选择的基础，通过研究偏微分方程的影响区域，从而为上述问题的解决提供理论支撑具有十分重要的意义。

2.3.1 抛物型方程

对于抛物型方程，初始时刻一点的影响区域是该时间点以后的整个空间，同样一点的依赖区域也是整个空间以前时段的函数分布。

2.3.2 双曲型方程

双曲方程式（10）在三角形区域内的解 u（x，t）由［x1，x2］上的初值分布惟一地决定，而与此区间以外的初值无关。参见图1，A点决定域为三角形ABC所围成的区域，BC的影响区域为两条点画线所确定的区域。对于大坝安全监控而言，影响区域内所测到的物理量与 BC区域初始条件是相关的，但不能由 BC区域唯一确定，不能建立确定性函数关系。决定区域的监测物理量是由 BC区域物理量唯一确定的，两者之间可以建立相应的函数关系。在考虑仪器监测误差的条件下，两者可以建立良好的统计模型。在影响区域外，监测物理量与 BC上的初始条件是独立的，也就是说不可能通过影响区域外的监测物理量反演到初始条件BC上的物理量。

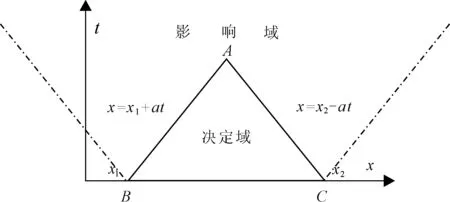
图1 线性双曲方程解的影响区域和决定域

对于高维双曲型方程，初始时刻一点的影响区域是以该点为顶点的、沿时间正向传播的特征锥面。一点的依赖区域是以该点为顶点的特征锥沿时间逆向直到初始时刻的特征锥所形成的球面。

对于线性双曲方程，由于边界条件的变化会在影响区域内得到相应的反映，因此通过影响区域内部的测点信息反馈分析以前时刻或边界区域的信息变化。对于非线性双曲方程，如浅水方程，即使边界条件是光滑的，解也可能存在间断，因此难以利用区域内部测值的连续性反映边界的连续性。

2.3.3 椭圆型方程

对于椭圆方程，边界曲面上任意小的影响区域都是整个区域。在边界上数据分布的不规则变化，经过整个区域的“平均”，影响的差别就不是很明显，如弹性力学理论中的S.Venant原理。在椭圆方程控制之下，区域 Ω相当于一个平滑滤波器，使得边界环境或荷载的变化在区域内的影响变得平滑，因此在椭圆方程控制的稳定温度场、稳定渗流场以及弹性力学中，要通过区域内有的有限点信息分辨边界的微弱变化必须采用高分辨率和灵敏度的仪器。

2.4 时间反演与信息传播速度

设在某些外界条件下按某种规律变化的一物理状态，在时间 t1时处于状态A，到时间t2时变为状态B；如果在 t2时刻的状态B可以沿着相反的变化过程回复到原来的状态A，而外界条件不发生其他的变化，则这物理状态的变化过程是可逆的，否则是不可逆的。

2.4.1 抛物型方程

抛物方程是不可逆的，信息传播的速度是无穷大。因此从理论上讲，只要仪器足够灵敏，可以立即“捕捉”到远处热源及其边界的变化。

在形式上，热传导方程出现对时间 t的一阶偏导数，在取 －t时，方程不具有等价性。物理上，热传导方程描述的是一个不可逆过程，物理上，热传导方程描述不可逆过程，不可能根据t＝0时刻的状态反推 t＜0的状态，从方程本身的形式来看，由于热传导方程仅出现 t的一阶偏导，故对时间反演不具有不变性。数学上表现为由 t2（t2＞t1）状态反演 t1状态的问题为不适定问题。

2.4.2 双曲型方程

波动方程则出现 t的二阶偏导，对时间具有不变性，可从t＝0的波动状态反推知 t＜0的波动状态，因此齐次线性波动方程具有时间对称性，其信息传播满足一定的速度，即波速 c。波动方程含有对时间的二阶导数，因此齐次方程形式上具有等价性，因此具有对时间反不变性，即可以从由 t2（t2＞ t1）状态反演 t1状态。意味着，在时间 t以后，ct半径范围内可以获得震源信息。但如果双曲波动方程中含有不可逆的阻尼项或耗散项，双曲方程也是时间反演不可逆的。

2.4.3 椭圆型方程

椭圆方程是对稳定状态下的描述，与时间无关，不存在时间反演对称性和信息传播速度问题。因此在大坝安全监控中，不可能利用稳态情况反演材料或结构动态流变（蠕变）信息。

3 结 语

一个偏微分方程的全面描述还包括初始条件、边界条件和满足区域，这些都有可能与偏微分方程的性质，特别是解的性质有密切的关系，而解的性质对应着大坝安全性态。随着大坝安全性态的不断演化，相应的偏微分方程无论在系数、方程形式，还是在类型上都有相应的改变本文重点以大坝安全监控中常见的二阶线性偏微分方程为例，叙述了其解析性质对大坝安全监控测值分析、仪器布置和误差估计等方面的意义。实际上，偏微分方程的性质还有很多，如解的Blow－up的临界指标和有限Blow－up的性质等［18］，更加复杂的问题将另文叙述。总之，通过研究偏微分方程的性质从而指导大坝安全监控工作具有十分重要的意义。

［1］ 方卫华.大坝安全监控：问题，观点与方法［M］.南京：河海大学出版社，2013.

［2］ 谷超豪，李大潜.数学物理方程（第二版）［M］.北京：高等教育出版社，2002.

［3］ 程建春.数学物理方程及其近似方法［M］.北京：科学出版社，2004.

［4］ 彭 华，陈胜宏 .饱和—非饱和岩土非稳定渗流有限元分析研究［J］.水动力学研究与进展A辑，2002，17（2）：253－259.

［5］ 盛金昌，速宝玉，王 媛.裂隙岩体渗流－弹塑性应力耦合分析［J］.岩石力学与工程学报，2000，19（3）：304－309.

［6］ Sheng D.Review of fundamental principles inmodeling unsaturated soil behavior［J］.Computers and Geotechnics，2011，38（6）：757－776.

［7］ Lloret A，Alonso E E.Consolidation of unsaturated soils including swelling and collapse behavior［J］.Géotechnique，1980，30（4）：449－477.

［8］ Chang C S，Duncan JM.Consolidation analysis for partly saturated clay by using an elastic－plastic effective stress－strain model［J］.International Journal for Numerical and Analytical MethodsGeomechanics，1983，7（1）：39－55.

［9］ Huang S，Barbour S L，Fredlund D G.Development and verification of a coefficient of permeability function for a deformable unsaturated soil［J］.CanadianGeotechnical Journal，1998，35（3）：411－425.

［10］ 徐芝纶.弹性力学（第二版）［M］.北京：高等教育出版社，1984.

［11］ WuW，LiX，Charier R，etal.A thermo－hydro－mechanical constitutivemodel and its numericalmodelling for unsaturated soils［J］.Computers and Geotechnics，2004，31（2）：155－167.

［12］ 陈恕行.高维非线性守恒律方程组［J］.中国科学：数学，2013，43（4）：317－332.

［13］ 高学平.高等流体力学［M］.天津：天津大学出版社 ，2005.

［14］ Sideris T C.Formation of singularities in three－dimensional compressible fluids［J］.Comm.Math.Phys.，1985，101（4）：475－485.

［15］ 林长好.一类二阶抛物方程解的极值原理和界［J］.中山大学学报，1986，（3）：50－54.

［16］ 吕 坤.微分方程的最大值原理及应用［D］.重庆：重庆邮电学院，2005.

［17］ 翟 健.偏微分方程引论［R］.杭州：浙江大学，2013.

［18］ 徐淑奖.几类非线性偏微分方程解法及解的性质的探讨［D］.北京：北京邮电大学，2006.

The Significance of Partial Differential Equation on Dam Safety Monitoring

FANGWei－hua1，2
（1.School of Science，Nanjing University of Science and Technology，Nanjing，Jiangsu 210094，China；2.Nanjing Automation Institute ofWater Conservancy&Hydrology，Nanjing，Jiangsu 210012，China）

In order to reinforce the basic theory of dam safetymonitoring，taking the solution propertiesof typical second order linear partial differentialequation asan example，maximum principle，uniquenessand stability of the solutions，affected region and time－reversal symmetry，were analysed to provide theoretical guidance on dam safetymonitoring includingmeasured value analysis，monitoring instruments arrangement，instruments range selection，and error estimate，etc.The analysis results show that the familiaritywith partialdifferentialequation playsan important role in improving the theoretical level of dam safetymonitoring.

partial differential equation；dam safety monitoring；modeling；error estimate

TV698.2＋39

A

1672—1144（2014）04—0088—06

10.3969／j.issn.1672－1144.2014.04.016

2014－02－28

2014－04－02

中央级公益性科研院所基本科研业务经费面上项目（Y913012）；科技部农业科技成果转化资金项目（2013GB23320631）；南京水利水文自动化研究所科研项目（ZL081108）

方卫华（1972—），男，安徽安庆人，博士后，高级工程师，硕士生导师，主要从事工程力学和工程安全监控方面的教学和科研工作。