基于定子磁链定向的双馈风力发电解耦控制研究

高扬，于会群，张浩，彭道刚

（上海电力学院自动化工程学院上海市电站自动化技术重点实验室，上海200090）

基于定子磁链定向的双馈风力发电解耦控制研究

高扬，于会群，张浩，彭道刚

（上海电力学院自动化工程学院上海市电站自动化技术重点实验室，上海200090）

首先介绍了变速恒频双馈风力发电系统的特点，构建了实际风速的数学模型，研究了基于定子磁链定向的变速恒频双馈风力发电机转子侧变换器的控制，最后仿真实现了双馈电机有功功率和无功功率的独立解耦控制，并在发电机定子侧输出单位功率因数的情况下，调节直流母线电压快速达到了给定参考值，维持了直流母线电压的稳定。

双馈感应风力发电系统；风速数学模型；定子磁链定向；有功无功解耦

1 引言

过去世界各地使用的风机，大多采用定速恒频风力发电机。定速恒频风力发电机通常采用常见的感应发电机，风速改变时，发电机的转速基本不变，运行在超同步情况下，转子的转差率s是负的，具有结构简单，维护方便等优点。但是，由于其转速恒定，不能跟踪最大风能，发电效率较低。风速改变时，发电机的功率波动也较大。当风速大于额定风速时，将会给风机的传动部分等造成很大的机械应力，可能损坏风机。电网电压发生闪变或者无功功率波动时，对发电机的电能质量也会产生影响。正常运行时不能改变电压，不利于电压恢复或者电力系统的稳定［1-3］。

目前广泛采用的变速恒频风力发电机，可以通过改变桨距角来调节风机的转速，进而调节发电机转子转速。变速恒频风力发电机主要通过绕线式转子上的电力电子器件，调节输出到电网上的有功功率和无功功率，根据风速变化，快速跟踪最大风能，提高发电效率。当电网电压闪变或者电网频率改变时，通过基于定子磁链定向的矢量控制技术对发电机定子输出的有功和无功功率进行解耦控制，调节电能质量。

2 基于定子磁链定向的矢量控制

变速双馈风机风力发电系统的基本结构如图1所示。风力机机轴通过增速齿轮箱连接到绕线式感应电机的转子上。电机定子直接连接到电网上，而转子通过交-直-交变频器连接到电网上。这些电力电子器件仅从电网上吸收约25%～30%的功率来实现对发电机的变速恒频控制。

图1 双馈电机风力发电系统结构Fig.1 Double-fed induction generator system

由于变速恒频双馈感应发电机的电路存在磁路上的耦合，为了实现有功功率和无功功率的解耦，采用了矢量控制，将三相静止坐标系下的定子三相电流进行d-q旋转坐标变换，分解为励磁电流分量和转矩电流分量。类似直流电机的转矩控制，在调速过程中，保持励磁电流分量不变，改变转矩电流分量控制电磁转矩，进行调速。

设d-q轴以同步速度旋转，转子和定子的电压和磁链方程按电动机惯例为

式中：uds，uqs，udr，uqr分别为定子和转子电压的d，q轴分量；Rs，Rr分别为定子和转子的电阻；ids，iqs，idr，iqr分别为定子和转子电流的d，q轴分量；p为微分算子；Ψds，Ψqs，Ψdr，Ψqr分别为定子和转子磁链的d，q轴分量；ω1，ωs分别为同步速和转差速度；Ls，Lr，Lm分别为定子和转子的自感及互感［4-6］。

如果将发电机的转子磁链定向在同步坐标系的d轴上，定子的有功功率和无功功率的计算就比较复杂，影响了控制系统的实时处理。为解决这个问题，将发电机的定子磁链定向在d轴上。由于双馈电机定子侧电流频率始终在50Hz左右，定子电阻的压降远比电机的反电势小，故可以忽略电机定子绕组的电阻，那么，定子电压方程就可以化简为

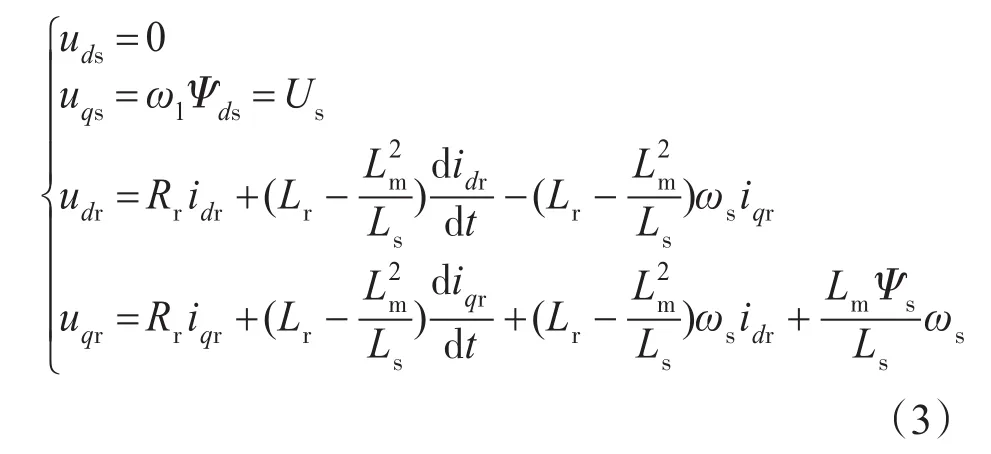
转矩方程为

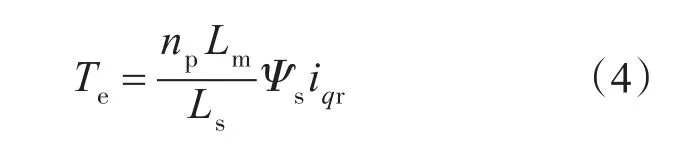
定子侧有功功率和无功功率分别为

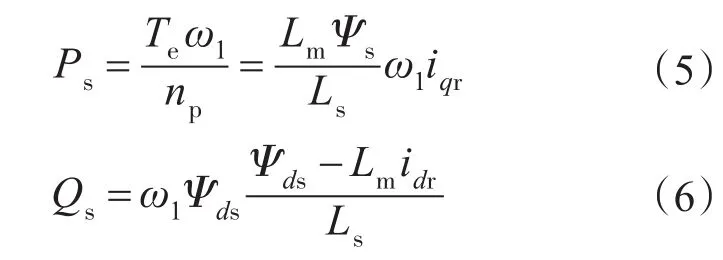
由式（5）可以看出，双馈发电机定子的有功功率与转子电流的转矩分量成线性关系。由式（6）可以看出，定子的无功功率与转子电流的励磁分量成线性关系。调节转子电流的转矩分量和励磁分量，就可以分别控制定子的有功功率和无功功率，实现有功功率和无功功率的解耦控制［7-9］。

有功和无功解耦控制策略如图2所示。

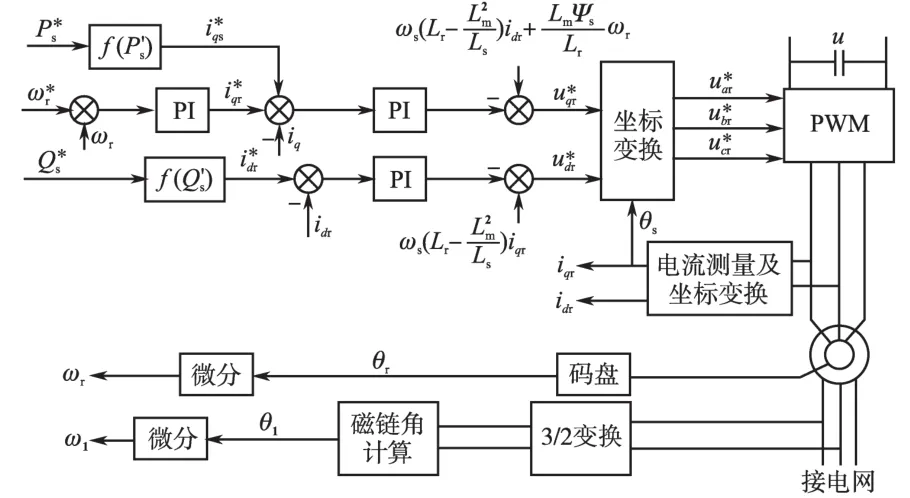
图2 变速恒频双馈风力发电机有功、无功解耦Fig.2 Active and reactive power decoupling of VSCF doubly-fed wind power generator

定子磁链即d轴位置的观测是矢量控制中旋转变换的关键。在静止坐标系下，忽略定子电阻后定子电压方程为

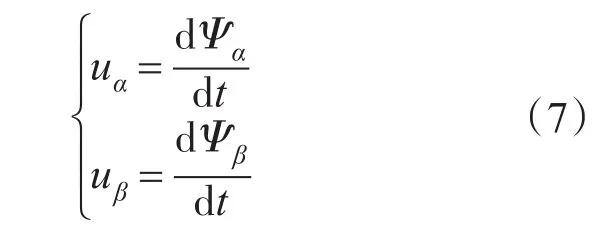
由式（7）可以看出，定子电压矢量超前定子磁链矢量90°，由观测到的定子三相电压经过3/2变换，得到静止坐标系下定子电压uα和uβ，然后计算出定子电压矢量给定位置角θ，定子磁链矢量位置为θ1=θ-90°，这样就可以得出坐标系d轴的位置。

3 仿真研究

3.1 风速数学模型

由于风能具有随机性和间歇性，通常将风速分解为基本风ν、阵风vWG、渐变风vWR和随机风vWN4个分量［10-12］。

基本风风速模型如下：

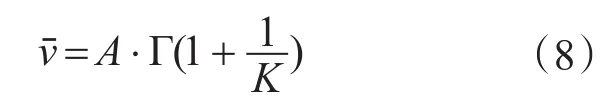
式中：A，K分别为Weibull分布的尺度和形状参数；Γ(·)为伽马函数。

基本风随时间t变化很小［13-14］，可以设定其为常数。

阵风风速模型如下：

式中：vWG为阵风风速，m/s；T1G为阵风启动时间，s；TG为阵风周期，s；vmaxG为阵风最大值，m/s；t为时间。

渐变风风速模型如下：

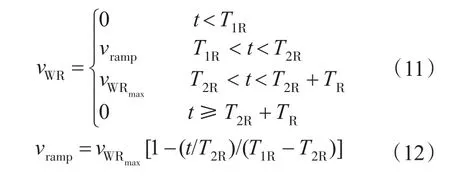
式中：vWR为渐变风风速，m/s；vWRmax为渐变风风速的最大值，m/s；T1R为渐变风启动时间，s；T2R为渐变风终止时间，s；TR为渐变风保持时间，s。

随机风渐变风风速模型如下：

式中：vWN为随机风风速，m/s；ωi为各个频率段的频率,，Δω为随机分量的离散间距；φi为0～2π之间均匀分布的随机变量；KN为地表粗糙系数；F为扰动范围，m2；μ为相对高度的平均风速，m/s；N为频谱取样点数。

综合上述4种风速成份，风力机上的风速可由4者来合成：

3.2 仿真参数设置

双馈风力发电系统的仿真参数设置如下：发电机的额定功率1 500kW，额定电压U=0.575kV额定频率f=50Hz，定子电阻Rs和定子漏感L1s分别为0.023（标幺值）和0.18（标幺值）；转子电阻Rr和转子漏感L1r分别为0.016（标幺值）和0.16（标幺值）；激磁电感LM为2.9（标幺值），双馈电机的极对数为3，转动惯量J=0.089kg·m2，风力机的风轮半径R＝2.4 m，齿轮传动比N=8，直流母线电压初始值为800V，开关周期Ts=0.000 2 s，仿真时间8 s。平均风速为8.5m/s时，最佳叶尖速比λopt=9，最大风能利用系数Cpmax=0.48。

3.3 仿真结果及分析

图3反映了风速的变化。基本风速为7.5m/s阵风从0 s开始，8 s结束，最大值为1m/s；渐变风从0s开始，4 s结束，最大值为1m/s，保持时间为4 s。图4和图5分别为定、转子三相电流仿真结果。

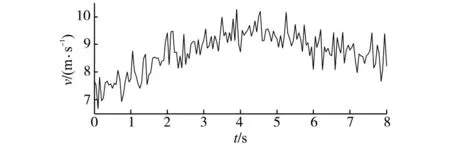
图3 风速仿真结果Fig.3 Simulation results of wind speed

图4 定子三相电流Fig.4 The three-phase current of stator

图5 转子三相电流Fig.5 The three-phase current of rotor

图6为有功功率和无功功率的控制结果。从图6可以看出，经过短暂的调节过程之后，定子有功功率和无功功率很快就实现了解耦控制［15-16］随着发电机转速的变化，定子有功功率虽然发生了改变，但能快速跟踪转速的变化，动态响应很快，而无功功率基本稳定，维持在0附近。这说明定子有功功率和无功功率实现了各自的独立调节。

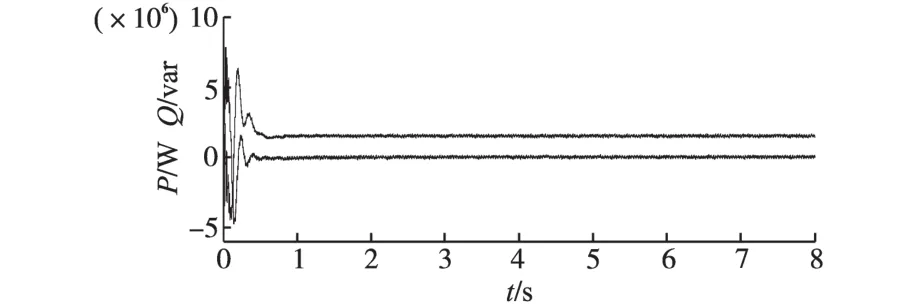
图6 定子有功功率、无功功率Fig.6 Active power，reactive power output of the stator

图7为直流母线电压的仿真结果。随着风速波动，直流母线电压很快从初始电压800 V达到给定电压参考值1 150 V。

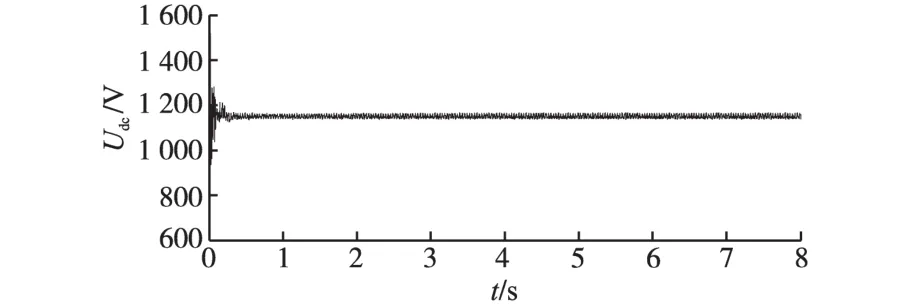
图7 直流母线电压Fig.7 Voltage of DC bus

4 结论

本文分析了风力机最大跟踪的控制方法，建立了包括基本风、渐变风、阵风、随机风等在内的真实情况下的风速仿真模型，探讨了双馈风力发电机有功和无功的独立解耦控制策略。

由于传统的PID控制是针对一个特定固定频率的线性化模型，而变速恒频双馈的风力发电系统是非线性的，时变不确定的，难以建立精确的数学模型，因此，后续仍需对双馈风力发电系统中并网控制和变桨距控制中的PID控制器作进一步的改进。

［1］王昌存.变速恒频双馈风力发电系统的研究［D］.哈尔滨：哈尔滨理工大学，2007.

［2］Sun Yuanzhang，Lin Jin，Li Guojie.A Survey on the Grid Integration of Wind Farms with Variable Speed Wind Plant Systems［J］.Automation of Electric Power Systems，2010，34（3）：75-80.

［3］马幼捷，尹向前，周雪松，等.变速恒频双馈风电机组的控制策略研究［J］.电气传动，2008，38（4）：12-16.

［4］马小亮.风力发电机组的电气控制［J］.电工技术学报，2006，21（6）：11-16.

［6］赵栋利，郭金东，许洪华.变速恒频双馈风力发电机有功、无功解耦控制研究与实现［J］.太阳能学报，2006，27（2）：174-179.

［7］姚兴佳，韩嵩崟，赵希梅，等.变速恒频双馈风力发电机的最大风能追踪控制［J］.电气传动，2012，42（7）：57-60.

［8］邬冬临，佘岳，徐凤星，等.双馈风力发电机机侧变频器控制策略的研究［J］.电气传动，2013，43（5）：66-69.

［9］徐大平，肖运启，秦涛，等.变桨距型双馈风电机组并网控制及建模仿真［J］.电网技术，2008，32（6）：100-105.

［10］贺益康，胡家兵.双馈异步风力发电机并网运行中的几个热点问题［J］.中国电机工程学报，2012，32（27）：1-15.

［11］胡家兵，贺益康，刘其辉.基于最佳功率给定的最大风能追踪控制策略［J］.电力系统自动化，2005，29（24）：32-38.

［12］刘其辉，贺益康，赵仁德.变速恒频风力发电系统最大风能追踪控制［J］.电力系统自动化，2003，27（20）：62-67.

［13］卞松江，吕晓美，相会杰，等.交流励磁变速恒频风力发电系统控制策略的仿真研究［J］.中国电机工程学报，2005，25（16）：57-62.

［14］黄晟，廖武，黄科元.双馈风力发电系统无速度传感器控制［J］.电气传动，2010，40（3）：3-5.

［15］王志新，张华强.风力发电技术与功率控制策略研究［J］.自动化仪表，2008，l29（11）：1-6.

［16］倪昊.变速变桨风力发电系统的控制［D］.兰州：兰州理工大学，2012.

Research on the Decoupling Control of Doubly-fed Wind Power Generators Based on Stator Flux Oriention

GAO Yang，YU Hui-qun，ZHANG Hao，PENG Dao-gang
（College of Automation Engineering，Shanghai Key Laboratory of Power Station Technology，Shanghai University of Electric Power，Shanghai 200090，China）

Firstly introduced the features of VSCF（variable speed constant frequency）doubly fed wind power generation system.Then the rotor side converter control based on the stator flux orientation was studied，achieved active and reactive power decoupling in the simulation.Finally，the output power factor of the generator stator was set as one，and the DC bus voltage was quickly regulated to the given reference value，maintaining the stability of the DC bus voltage.

doubly fed induction wind power system；wind speed model；stator flux orientation；active and reactive power decoupling

TM614

A

2014-01-06

修改稿日期：2014-06-11

国家自然科学基金重点项目（61034004）；上海市教育委员会科研创新项目（12YZ142）

高扬（1990-），男，硕士研究生，Email：jjgyxky@126.com