基于射击次数的编队防空队形优化配置
2014-07-07翁璐姚跃亭刘剑锋孟凡磊
翁璐,姚跃亭,刘剑锋,孟凡磊
(1.海军装备部,北京100841;2.海军航空工程学院飞行器工程系,山东烟台264001)
基于射击次数的编队防空队形优化配置
翁璐1,姚跃亭2,刘剑锋1,孟凡磊2
(1.海军装备部,北京100841;2.海军航空工程学院飞行器工程系,山东烟台264001)
为解决舰艇编队协同防空中抗击多方向来袭目标流的队形部署优化问题,提出了以编队对来袭目标流的综合射击次数为目标函数的优化方法。将编队总射击次数分解为零航路捷径和非零航路捷径下的射击次数之和,利用射击次数与、杀伤区纵深、队形配置向量之间的约束关系,给出了计算方法。以一字队形为例,建立了队形部署优化模型。
编队防空队形优化配置;射击次数;多方向目标流;一字队形
在舰艇编队协同防空中,良好的编队队形配置,是达到合理利用兵力、充分发挥火力、有效抗击敌空袭的重要条件,也是实施防空射击指挥决策的基本依托。编队队形配置是一个综合多种因素、寻求最佳方案的过程。这些因素包括:防空武器数量和性能、杀伤区耦合、敌来袭方向、对抗干扰、火力掩护区面积等。单独考虑某一个因素进行队形配置有失偏颇,很难得到正确的结果;因素太多,会使防空队形配置建模过程显得非常复杂。因此,需要一个综合性的指标,通过建立各种因素的约束关系模型,来合理准确地反映编队队形配置的优劣,
文献[1]以被掩护舰的生存概率为优化目标,建立了防御队形配置方法。但是该方法受敌我兵力使用方式影响较大。文献[2]从电子对抗、火力协同、指挥通信和区域掩护4个方面对对象配置进行了较为完整的研究。但对一些问题阐述还不够深入。文献[3]给出了航母编队防空哨戒阵位缺点原则。文献[4]则以防空区域防御纵深最优为目标,研究了双舰编队的扇面部署问题。但是航母编队往往规模较大,而双舰编队则规模太小,两者的研究成果都很难直接应用在常规驱护舰编队的防空队形配置中。
按一定队形配置的编队防空作战体系作为防御方,主要任务是在杀伤区内尽可能多地杀伤目标数,制止空袭目标突击编队或阻止目标通过编队杀伤区,使编队的安全系数或者生存概率最大。因此,编队防空系统杀伤目标期望可以较全面地衡量编队队形配置的优劣。该期望值是抗击连续空袭时,武器能拦截目标数量的最大值,由射击次数和杀伤目标概率决定。当给定目标流和防空武器参数时,该武器的杀伤概率即可确定。因此,射击次数即成为衡量防空火力配系优劣的一个核心指标。
本文依据这一特点,引入队形配置决策向量,给定多方向来袭的目标流,以一字队形为例,建立以总射击次数为目标函数的队形配置模型,旨在解决编队抗击多方向目标流的队形优化配置问题。
1 编队协同射击次数模型
1.1 单舰射击次数模型
当来袭目标航路捷径为零时,理想状态下,第1个弹目遭遇点恰好位于舰空导弹杀伤区远界上,最后1个弹目遭遇点恰好位于杀伤区近界上,则舰空导弹拦截射击次数为[5]

式中:Lyj、Ljj分别为舰空导弹武器系统杀伤区远界和近界;vd为舰空导弹的平均飞行速度;tΔ为舰空导弹发射间隔时间与该枚防空导弹飞行时间的差值;λ为目标平均飞行速度与舰空导弹平均速度之比值。
在非零航路捷径时,假定来袭目标以高度H、航路捷径P运动,如图1所示[6]。
图1中,O点为舰空导弹发射点位置,目标的航路捷径点记为CPA点。Ti点为第i枚防空导弹与目标遭遇时刻所在位置,i=0,1,…,N,N为舰空导弹武器系统的总射击次数;Di为该时刻目标在水平面内的斜距;θj为在弹目遭遇点处的目标角;αj为舰空导弹的前置射击角。依据图1的几何关系,当目标越过舰空导弹的杀伤区近界时,目标已突防,此时迎击的射击次数达到最大。则:

式(2)中[5]:
1.2 邻舰的掩护射击次数模型
假设来袭目标朝O1舰进攻,O2舰为掩护舰。图2中扇形区域ABC所围区域就是O2舰对O1舰的协同防空区域。在图2中所示的协同射击态势图中,目标相对O1、O2舰的航路捷径分别为P1、P2,则两舰的掩护射击次数可等效为各自对杀伤区纵深为M1M2的目标在非0航路捷径下进行射击的次数。
Lyj为O2舰的杀伤区远界,Qm为目标相对O1舰的舷角,Qmin为O1舰舰空导弹的最小射界,d为O1和O2两舰间距,θ为O1相对O2舷角,也称为看齐角。

图2 邻舰掩护杀伤区Fig.2 Diagrammatic sketch of adjacent ship covering kill zone
在理想情况下,M1点恰好位于防空导弹的杀伤区远界上,则协同射击时的第一个弹目遭遇应该位于M1点处。当目标越过M2点时,目标实现突防。此时,掩护射击次数达到最大,则掩护舰在非零航路捷径下的射击次数为[7]:

式(4)中,Li
1.3编队总射击次数模型
编队总射击次数是编队内各协同成员的射击次数之和。以双舰编队为例,来袭目标攻击其中一舰时,另一舰即为掩护舰,此时,编队总的射击次数就由被攻击舰对(零航路捷径)目标的射击次数与掩护舰对(非零航路捷径)目标的射击次数之和。当增加编队成员数目和来袭目标流数目时,对每一批目标,同样存在被攻击舰和掩护舰的集合。则编队总的射击次数Ntotal存在如下关系:

式(5)中:M为来袭目标流批数;Ni为编队抗击第i批目标的射击次数;B为能够抗击第i批目标的舰艇集合;B0为被攻击舰;B0¯为掩护舰集合,且满足

式(6)表明:编队抗击多批次、多方向来袭目标流时,预计的总射击次数是M个集合B的射击次数之和。当给定威胁目标和舰空导弹武器参数时,因为被攻击舰的抗击次数保持不变,编队总的射击次数就与掩护舰的射击次数相关。由1.2节分析可知,影响掩护舰射击次数的关键参数为该防空武器的杀伤区纵深。因此,可以利用该参数与队形配置向量、射击次数之间的约束关系建立综合配置模型。
2 编队对多方向目标流射击次数模型
编队队形是由编队成员在空间内的相对位置即舰艇之间的距离d和看齐角θ唯一确定的。其中,舰艇间隔距离主要影响编队的目标探测能力以及目标的防御纵深。看齐角则直接影响编队整体防御区域的大小和对目标的拦截效果。调整和改变编队队形,实际上就是改变d和θ,将编队火力单元进行合理配置,在重点部署区域将同型或异型的火力单元杀伤区进行耦合,能改善火力结构,提高集火能力。
双舰编队队形的一般研究方法都是假设编队防空导弹武器类型、性能一致,在给定威胁目标的情况下,协同杀伤区纵深最大对应的队形配置就是最优配置。但是,由于多舰编队的舰空导弹武器多种多样,协同杀伤区纵深计算方法与双舰编队的计算方法有较大区别,因而该方法不能直接应用于多舰编队的队形配置。
为获得多舰编队的更具广泛意义的驱护舰编队队形配置,设计优化方法思路为:给定威胁目标流,建立一字队形防空态势,引入队形配置向量进行杀伤区纵深计算,以编队所有舰艇对所有目标的总的射击次数为目标函数,在受约束的决策空间内寻找使目标函数达到最大的向量,即为最优的编队队形配置方案。当编队内舰空导弹武器系统不一致时,该A¯为一决策矩阵。
2.1 一字队形防空态势
现代舰艇编队防空的来袭目标流以导弹流为主。给定四个方向上的导弹流,认为该导弹流临空时间间隔的数学特性符合巴尔姆流[8],且在不同的突击样式下会呈现出不同的分布。假设编队序列为(J0,J1,J2,J3,J4),其中J0为被掩护的指挥舰,其余四艘舰艇为掩护舰。导弹流均向J0攻击,则忽略J0的防空能力,重点考察掩护舰的情况。J1、J2为护卫舰,装备了相同型号的中近程舰空导弹武器系统,J3、J4为驱逐舰,装备了相同型号的中远程舰空导弹武器系统,导弹武器均具有全向攻击能力。一字队形下编队抗击导弹流的态势图如图3所示。
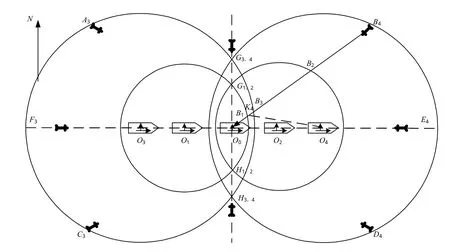
图3 一字队形编队抗击多方向目标流态势图Fig.3 Situation chart of fleet in line-type formation intercept multi-direction target flow
图3中来袭目标流序列为Mi,i=1,2,…,8,该序列的航向角为βi。编队队列线与正北方向的夹角为α,α=π/2。编队成员航向角保持一致。舰艇序列在过指挥舰质心的水平面内投影为:(O0,O1,O2,O3,O4)。集合(Ai,Bi,Ci,Di,Ei,Fi,Gi,Hi)为8批目标流航路与4艘掩护舰防空导弹杀伤区远界的交点(i=1,2,3,4)。
因为图3中坐标系的对称性,以第I象限的目标序列M2为例进行分析。该目标序列相对J0的舷角Qm02=α-β2。以O0为原点,以指挥舰艏艉线的延长线在水平面内的投影为X轴,舰艏方向为正;艏艉线的垂线在水平面内的投影为Y轴,向右方向为正,建立坐标系。不妨设0≤α≤π/2,则当目标航向角,坐标轴XOY沿顺时针方向旋转π/2-α,得到指向正东和正北方向的坐标轴X′OY′。对图3作简化处理,如图4所示。

图4 第I象限目标流的攻击态势图Fig.4 Engagement situation chart of first quadrant
2.2 一字队形优化配置模型
由图4知:掩护舰J4对目标流M2的杀伤区纵深为为J4受J2影响的禁危区边界,点K4为该目标流航路与的交点。利用三角关系,有:

a4、b4为J4受该禁危区影响的射界直线参数为该射界线与禁危区的交点坐标。

同理,可得:

同理,可得到J1和J3对该目标流的杀伤区纵深计算式。虽然目标流航路B4O0与J1和J3的杀伤区远界存在交点,但是由于该交点可能位于邻舰影响的射击禁危区内,导致不能对M1进行抗击。因此,必须对该交点进行禁危区判断,即:
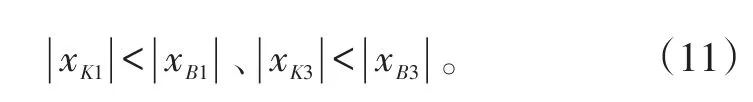
式(11)中:xB1、xB3为J1、J3杀伤区远界与目标流交点的横坐标;xK1、xK3为目标流航路与J1、J3禁危区边界交点的横坐标。
成一字队形时通常满足:d1=d2,d3=d4。
令Qmij为目标i相对舰艇j的舷角。当编队成一字队形时,θ=0。可建立第一象限的编队总射击次数计算模型:

式(12)中,对被攻击舰艇,采用式1的零航路捷径射击次数计算式;对掩护舰,采用式2~4的非零航路捷径射击次数计算式。
以上给出的是在给定防空武器系统配置的情况下,编队对以一定方位角进入防空区域的单个目标序列的射击次数计算方法。假设在图4所示的90°范围内,目标进入方位角服从分布密度函数为的某一分布,则在整个图3所示的圆周区域内,编队抗击多方向目标流的总射击次数期望为:

上式与式(12)具有相同的变量约束。
3 仿真分析
对图4所示的攻击态势,依据文献[9],设来袭目标为反舰导弹,vt为330 m/s,飞行高度为30 m,β2为30°,α为60°,假设舰艇间距相等,即d=d2=d4-d2,J2、J4的舰空导弹飞行速度均为1 000 m/s,舰空导弹武器系统为单通道系统且具有全向攻击能力[10],杀伤区远界分别为12km和15km。令舰艇间距d在0~ 120链范围内变化,得到仿真结果如图5所示。图中,纵轴表示J2和J4舰对来袭目标的射击次数之和,横轴为d。舰艇间隔距离单位为链(Cab=10-1nmile)。由图5知,当舰艇间距从0逐渐增大时,J2和J4对目标流的杀伤区纵深增大。但是,在(0,280)Cab内,两舰对目标的抗击可以近似为0航路捷径的抗击过程,所增加的纵深尚不足以使舰空导弹完成一次完整的射击周期,因而总射击次数保持不变。在(28,46)Cab内,间距对总射击次数的影响较大,从8.2次增大到了13.3次。在间距d约为41 Cab处,J0舰恰好位于J4舰杀伤区远界上,此时,J4舰对目标的射击次数达到最大,继续增大等间距d,则抗击目标的纵深逐渐减小,导致射击次数的逐渐降低。

图5 一字队形下J2和J4的射击次数Fig.5 Fire times ofJ2andJ4under line formation
图4中,当d4≈82 Cab,d2=41 Cab时,由于J2的杀伤区远界为12km,因而该舰对目标的杀伤区纵深依然具备增大的余地。此时,若保持J4舰的位置不动,继续增大d2,则总射击次数依将继续增大。当d2=65 Cab,d4=82 Cab时,总射击次数将达到14.8的最大值。
由于图4是一个简化态势图,仅表示了单个象限内的防空态势,且图5的仿真结果也只对目标流M2进行了仿真。实际在图3中,在第I象限内有3个目标流,分别是M1、M2和M3。由于M3位于队列线上,只能由J4舰单独进行抗击,因此,该象限实际能够协同抗击的目标流为M1和M2。M1位于J1和J2、J3和J4的耦合杀伤区内,该耦合杀伤区随着舰艇间距增大而减小。由于J2和J4对2个目标流的拦截过程具有相同特性,因而以J2舰为例进行仿真,得到图6。图6中,横轴为d2,纵轴为J2舰对2个目标流的射击次数。
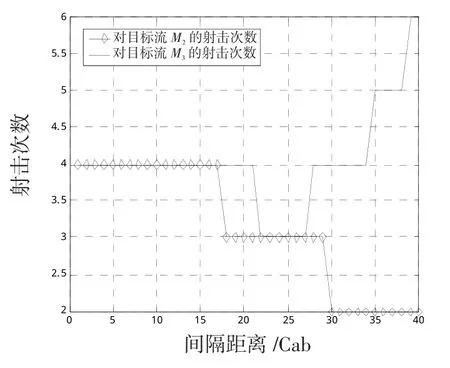
图6 第I象限2个方向来袭目标流射击次数与间距关系Fig.6 I llustration for fire frequency to ships intervals with two different direction targets flows in first quadrant
由图6可知,当d2较小时,J2舰对2个目标流的杀伤区纵深均为12km,因而射击次数也一致。d2逐渐增大,J2对M1的纵深逐渐减小,对M2的纵深B2O0分为二段,其中,B2O2随着d2的增大逐渐减小,而O2O0则逐渐增大,在增大至L2min之前,舰空导弹都不能对该目标流进行射击,因而J2的总射击次数仅与B2O2相关,与O2O0无关。因此,在d2达到21 Cab时,射击次数下降。此后d2继续增大,O2O0的距离也越过J2的杀伤区近界,使射击次数开始增加。当d2=42 Cab时,目标流相对J2舰空导弹的航路捷径为7.7km,超出了该型导弹能够拦截的最大航路捷径P2max,因而对M1的射击次数为0。
由以上讨论可以看出,对图4的防空态势,虽然增大舰艇间隔距离能够增加对队列线方向来袭目标流的射击次数,却相应的减小了对垂直于队列线方向来袭目标流的射击次数,因而对来袭方向不同分布的目标流需要采取不同的间隔距离配置方式。
0,30 Cab,L2jj=3km,对J2按照队形向量关系进行射击次数仿真,结果如图7所示。
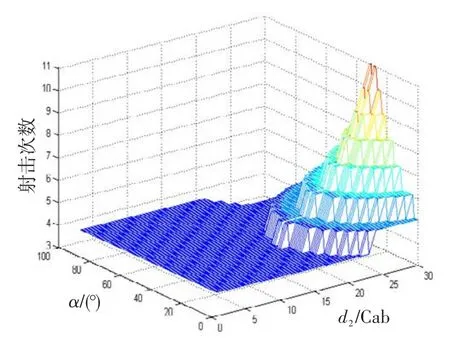
图7 不同队形配置下J2对M2的射击次数Fig.7 Fire times ofJ2toM2under different formation
图4中,给定目标流M2的航向角时,J2舰对目标流M2的射击次数与队列线的方位角相关。与只有迎击杀伤区的双舰协同情况不同,具有全向攻击能力的一字队形编队,相对舷角Qm02越小,队列线方位角越贴近目标流来袭方向,相应的射击纵深越大,射击次数也越大。当Qm02=0时,队列线与目标来袭方向重合,位于J2后方的区域为射击禁区,因而J2对目标流的射击纵深为Lyj,此时,射击次数下降到5次。
4 总结
海上编队防空队形配置是编队火力运用的重要问题之一。本文利用射击次数与杀伤区纵深、队形配置向量之间的约束关系,建立了一字队形优化配置模型,通过射击次数来衡量队形的优劣,并进行了仿真验证。为舰艇编队防空队形优化提供了新思路。
由于篇幅所限,本文仅就一字队形展开了建模仿真,下一步将把该优化配置模型的构建方法应用于其他典型防空队形,如菱形、人字形等,并针对具有区域防空导弹武器和近程防空导弹武器相结合的舰艇编队防空队形问题进行具体研究[11-12],以明确量化的指标实现几种队形的优劣评判,为编队防空作战指挥决策提供参考。
[1]李永刚.舰艇编队对空防御队形优化配置模[J].情报指挥控制系统与仿真技术,2000,26(4):65-67. LI YONGGANG.A model of optimal disposition of warship formation for air defense[J].Information Command Control System&Simulation Technology,2000,26(4):65-67.(in Chinese)
[2]谭安胜,邱延鹏,汪德虎.新型驱护舰编队防空队形配置[J].火力与指挥控制,2003,28(6):5-9. TAN ANSHENG,QIU YANPENG,WANG DEHU.Investigation on air defense disposition for formation of destroyers and escort vessels[J].Fire Control&Command Control,2003,28(6):5-9.(in Chinese)
[3]徐胜良,王振波.航母编队航渡过程中防空哨戒舰阵位确定方法研究[J].指挥控制与仿真,2007,29(4):54-58. XU SHENGLIANG,WANG ZHENBO.Research on the position of air defense-guard ship for carrier formation during navigation[J].Command Control Simulation,2007,29(4):54-58.(in Chinese)
[4]赵建印,刘芳.海上编队双舰防空队形部署优化研究[J].兵工学报,2010,31(6):865-869. ZHAO JIANYIN,LIU FANG.Deployment optimization of two warships formation for air defense[J].Acta ArmamentarⅡ.2010,31(6):865-869.(in Chinese)
[5]丹尼尔·瓦格纳,查尔斯·米兰德.海军运筹分析[M].姜青山,郑保华,译.北京:国防工业出版社,2009:286-298. DANIEL H WAGNER,W CHARLES MYLANDER.Naval operation analysis[M].Traslated by JIANG QINGSHAN,ZHEN BAOHUA.Beijing:National Defense Industry Press,2009:286-298.(in Chinese)
[6]谭安胜.水面舰艇编队作战运筹分析[M].北京:国防工业出版社,2009:221-240.(in Chinese)TAN ANSHENG.Surface fleet operation analysis[M]. Beijing:National Defense Industry Press,2009:221-240.(in Chinese)
[7]范英飚,姚跃亭,高波.舰艇编队协同防空连续射击次数仿真分析[J].计算机工程与设计,2011,32(6):2092-2095. FAN YINGBIAO,YAO YUETING,GAO BO.Analysis and simulation on continuous fire frequency of coordinate air defense in warship formation[J].Computer Engineering and Design,2011,32(6):2092-2095.(in Chinese)
[8]高山,李孝军,陈杰生.面向防空的空袭目标流时间特性分析[J].空军工程大学学报:自然科学版,2008,9(1):41-45. GAO SHAN,LI XIAOJUN,CHEN JIESHENG.The analysis of time characteristic of air-raid target stream for air defense[J].Journal of Air Force Engineering University:Natural Science Edition,2008,9(1):41-45.(in Chinese)
[9]高雁翎,施荣,黄莉茹,等.世界防空反导导弹手册[K].北京:国防工业出版社,2010:410-413. GAO YANLIN,SHI RONG,HUANG LIRU,et al.Manual of antimissile missile in the world[K].Beijing:National Defense Industry Press,2010:410-413.(in Chinese)
[10]沈治河,杜一平.关于水面舰艇编队防空队形的研究[J].海军大连舰艇学院学报,1996,19(3):17-19. SHEN ZHIHE,DU YIPING.Study on surface fleet antiair formation[J].Journal of Dalian NavalAcademy,1996,19(3):17-19.(in Chinese)
[11]马雷挺,熊吉光.有区域防空导弹的驱护舰编队防空队形研究[J].海军大连舰艇学院学报,2000,23(4):10-12. MA LEITING,XIONG JIGUANG.Study on anti-air formation of surface fleet with area air defense missile[J]. Journal of Dalian Naval Academy,2000,23(4):10-12.(in Chinese)
[12]马其东,方立恭.海上区域防空目标威胁评估模型[J].现代防御技术,2009,37(1):15-19. MA QIDONG,FANGN LIGONG.Research on threat assessment model of air target for area air defense[J].Modern Defence Technology,2009,37(1):15-19.(in Chinese)
Optimal Allocation of Anti-Air Warships Formation Based on Fire Times
WENG Lu1,YAO Yue-ting2,LIU Jian-feng1,MENG Fan-lei2
(1.Naval Equipment Department,Beijing 100841,China; 2.Department of Airborne Vehicle Engineering,NAAU,Yantai Shandong 264001,China)
An optimal method using firing times to the target flow as objective function was brought forward.The objective function was divided into two parts,one with zero course shortcut and another with none zero course shortcut.And the calculate method was given with the bounded relation between firing times,kill zone depth and formation deployment vector. Taking the trail formation as an example,the optimal model was constructed.
anti-air warships formation optimal allocation;fire times;multi-direction targets flow;trail formation
E928.674
A
1673-1522(2014)01-0087-06
10.7682/j.issn.1673-1522.2014.01.019
2013-10-20;
2013-12-10
翁璐(1979-),男,硕士。
Key words:
