空舰导弹射击禁区计算模型
2014-07-07帅鹏刘铁文建国
帅鹏,刘铁,文建国
(1.海军装备部,北京100071;2.海军航空工程学院a.飞行器工程系;b.科研部,山东烟台264001)
空舰导弹射击禁区计算模型
帅鹏1,刘铁2a,文建国2b
(1.海军装备部,北京100071;2.海军航空工程学院a.飞行器工程系;b.科研部,山东烟台264001)
空舰导弹射程远、飞行过程中的干扰因素多,明确其实弹射击过程中的禁区对于指导部队的射击训练和作战使用具有重要意义。文章通过分析空舰导弹武器系统的特性,梳理归纳了影响空舰导弹射击禁区的主要因素;在分析空舰导弹运动特性的基础上,采用质点飞行弹道模拟法、导弹飞行误差合成法建立了空舰导弹射击禁区的计算模型。
空舰导弹;射击禁区;计算模型
部队在组织空舰导弹实弹射击和打靶时,面临最大的问题就是难以准确可靠地确定空舰导弹的射击禁区,只能依据有限的弹道数据进行大致估算。这样如果估算的禁区范围过小,在实弹射击时助推器和导弹残骸有可能对禁区外的保障舰艇及民船造成伤害;如果估算的范围过大,又会导致前期投入扫海和保障的兵力过多,费时费力,严重影响了训练和试验任务的开展,有时甚至因为保障兵力不够而让民用船只误驶入射击禁区,导致训练任务紧急中止[1]。
为了保证部队实弹射击训练和打靶试验任务能安全有效地开展,必须能够科学合理地确定空舰导弹的射击禁区,解除部队训练时的后顾之忧,使部队官兵能通过实弹射击训练熟练掌握武器装备的性能,提升部队战斗力。
1 射击禁区定义及影响因素
1.1 射击禁区定义
空舰导弹射击禁区是包括导弹助推器脱落区和末制导雷达搜索、捕捉、自导命中的区域,以及导弹正常飞行的区域,对射击禁区区域的计算就是计算导弹在系统各种误差和自然环境干扰作用下正常飞行的区域以及助推器坠落区域。
1.2 影响因素
在具体划定空舰导弹射击禁区之前,首先需要对影响空舰导弹射击禁区划定的各种因素加以分析。影响空舰导弹射击禁区划定的因素有很多,根据其制导体制、性能参数、工作过程以及射击禁区形成的原因,大体上可以将这些因素归纳为以下3类。
1)自然环境因素。自然环境的因素主要包括:大气温度和风。气温主要影响导弹的飞行速度,造成导弹自控终点在距离上散布的变化,从而对导弹的禁区造成影响[2-3]。气温对空舰导弹飞行速度的影响可以总结为:气温升高,导弹飞行速度增大,飞行时间减小;气温降低,飞行速度减小,飞行时间增加。温度变化时飞行时间变化规律,可由如下经验公式获得:
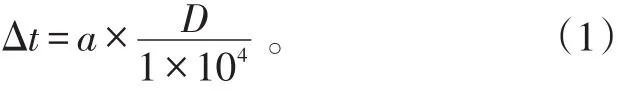
式(1)中:a为系数;D为导弹飞行距离;Δt为相对于发射点温度的变化值。
风对导弹射击禁区的影响主要体现在对导弹飞行弹道的影响上。其作用效果等效为导弹受到纵风和横风2个方向外力的共同作用。导弹飞行过程中,由常值风造成的飞行最大偏差可按发射条件允许的最大风速计算,以全程横风或全程纵风影响为最大。Ewx=Fxm·t;(2)Ewz=Fzm·t。(3)式(2)、(3)中:Ewx、Ewz分别为由常值风造成的纵向和侧向飞行最大偏差;Fxm、Fzm分别为发射条件允许的最大纵向风速和侧向风速。
2)载机因素。影响禁区大小的载机因素包括:载机的发射点散布,载机发射导弹时的扇面角,载机的发射航向角误差,载机发射导弹时的飞行速度和飞行高度等[4-6]。
载机定位误差区域:发射点为中心点,半径为Ez的圆,即Ezx=Ezz=Ez,Ezx、Ezz分别为载机纵向和侧向定位误差。
扇面发射角ψ:根据导弹允许发射条件,最大扇面发射角为α;发射航向角最大误差Eφ取β。
3)导弹系统因素。影响禁区大小的导弹因素主要包括:导弹系统误差、导弹末制导雷达的搜索范围、动力航程、弹道高度、导弹最大飞行时间。
导弹系统误差主要有惯导误差和制造误差。惯导误差包括初始对准时产生的误差和飞行过程中的累计误差。初始对准误差可由惯导性能参数直接获得。累计误差则需要根据惯导系统的极限误差结合导弹飞行距离确定。惯导系统的极限误差一般按最大飞行时间给定,据此可以将其转换为单位误差,并将惯导累计误差看作工作时间的非线性关系。具体可由下式得到:式(4)中:Egx、Egz分别为惯导纵向、侧向累计误差;Sgx、Sgz分别为惯导纵向、侧向极限误差;td、tmax分别为导弹实际飞行时间和最大飞行时间。
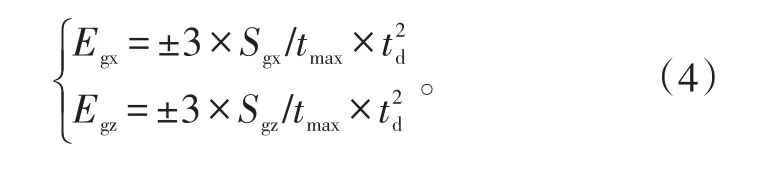
由于制造误差涉及因素众多,一一分析无必要,可以简化取其与惯导精度相同,则导弹系统误差为:Esx=2Egx;(5)Esz=2Egz。(6)式(5)、(6)中,Esx、Esz分别为导弹纵向、侧向系统误差。
2 空舰导弹射击禁区计算模型
2.1 空舰导弹弹道划分
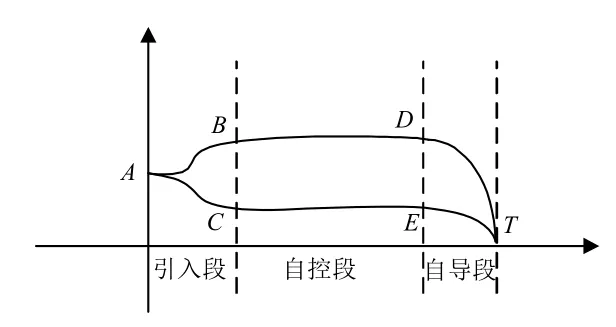
图1 各段飞行区域示意图Fig.1 Schematic diagram of each flight zone
空舰导弹的典型弹道可分2种情况,如图1所示。一种是高空飞行的弹道ABDT,另一种是低空飞行的弹道ACET[7]。
空舰导弹的典型弹道包括以下3部分。
第Ⅰ段为引入段。即导弹从载机上投射后,至高度信号接入控制回路时的弹道。采用低空飞行弹道时导弹发射后即下滑到预定高度后(见图1中的C点),高度信号接入,导弹转为程序控制,AC段即为引入段;采用高空飞行弹道时,导弹离开母机后,先稍下滑一小段再爬升,当爬升到预定高度后(见图1中的B点)高度信号接入,导弹转为程序控制,AB段即为引入段。
第Ⅱ段为自控段。即导弹开始进行程序控制起,至导引头开机时的飞行弹道。
第Ⅲ段为自导段。即导引头开机搜索捕捉目标起,至导弹命中目标时的飞行弹道。
空舰导弹侧向正常飞行区域主要包括:导弹引入飞行及助推器脱落区域、自控飞行区域、自导飞行区域3个部分在海平面上的投影(不带助推器的导弹没有助推器脱落区域)。
空舰导弹禁区的计算包括:引入段、自控段、自导段、按最大飞行时间飞行段和助推器脱落段。引入段的终点也是自控段的起点,而自控段的终点也是自导段的起点。由于误差是呈圆形散布的,为区域划分方便起见,各段起点和终点的散布以散布圆外切矩形的形式给出,如图2所示。
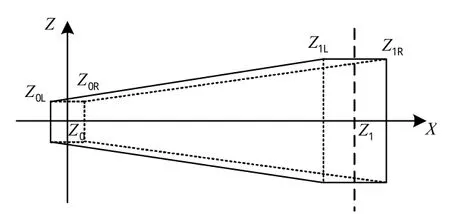
图2 各段飞行区域示意图Fig.2 Schematic diagram of each flight zone
图2中,Z0点为导弹各段理论飞行起点,Z0X轴为导弹预定射向,Z0Z轴垂直于Z0X轴;左边矩形为起点散布圆的外切包络,Z0L点为起点散布左边界点,Z0R点为起点散布右边界点;Z1点为导弹各段理论飞行终点,右边矩形为终点散布圆的外切包络,Z1L点为终点散布左边界点,Z1R点为终点散布右边界点。
2.2 引入段飞行区域
导弹引入段飞行区域是指导弹“离机”至飞行到t1(引入段飞行时间)时导弹的正常飞行区域。
引入段飞行区域按有无助推器分2种情形。
1)有助推器。
考虑到助推器脱落后坠落区域的计算需要获取助推器脱落点的相关参数,设t11为导弹发射至助推器工作时间,t12为助推器脱落至高度信号接入时间,则引入段飞行时间t1=t11+t12。
0~t11(助推器脱落):导弹正常飞行距离Xd11=vd·t11,式中,vd为导弹飞行速度。为稳妥起见,vd取导弹平均飞行速度的最大值vdmax。
扇面发射角引起的侧向偏差为Eψ,z=vd·t11·sinψ。
由系统误差引起的纵向飞行偏差Esx11和侧向飞行偏差Esz11可根据式(5)和(6)计算获得。
发射航向角误差引起的侧向偏差为Eφ,z=vd·t11·sinEφ。
因此,在0~t11内,由扇面发射角、各种误差和环境干扰导致的导弹飞行偏差为:
Ex11=Esx·t11+Fxm·t11+vd·Δt;(7)
Ez11=Esz·t11+Fzm·t11+Eψ,z+Eφ,z。(8)
式(7)、(8)中:Ex11、Ez11分别为助推器工作段导弹飞行纵向和侧向偏差;Δt为大气温度变化引起的助推器工作时间的变化,可根据式(1)计算获得。
t11~t1(助推器脱落,至高度信号接入):导弹正常飞行距离Xd12=vd·t12。
此时助推器已经脱落,导弹根据设定弹道要求进行爬升或下滑,扇面发射角可逐渐修正,发射航向误差角也可消除,但已形成的位移不能消除。此段时间只有系统误差和风的干扰引起导弹的飞行偏差,其大小为:
Ex12=Esx·t12+Fxm·t12;(9)
Ez12=Esz·t12+Fzm·t12。(10)
式(9)、(10)中:Ex12、Ez12分别为t12时间段导弹飞行的纵向、侧向偏差。
引入段飞行起点后向边界端点位置为(-Xj1_0L,Zj1_0L)和(-Xj1_0L,-Zj1_0L),前向边界端点位置为(Xj1_0L,Zj1_0L)和(Xj1_0L,-Zj1_0L),其中:

引入段飞行终点散布后向边界端点位置为(Xj1_1L,Zj1_1L)和(Xj1_1L,-Zj1_1L),其中:
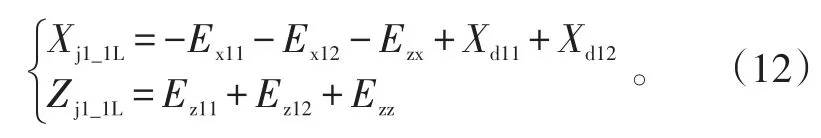
引入段飞行终点散布前向边界端点位置为(Xj1_1R,Zj1_1R)和(Xj1_1R,-Zj1_1R),其中:
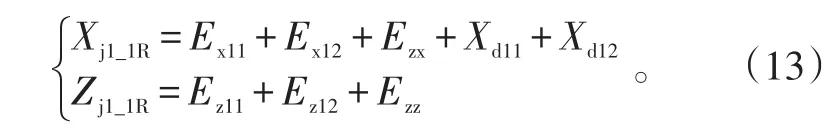
飞行终点后向边界端点是指靠近发射点的位置,飞行终点前向边界端点是指远离发射点的位置,以下含义均相同。
2)无助推器。
0~t1(高度信号接入):导弹正常飞行距离Xd1=vd·t1。
扇面发射角引起的侧向偏差:Eψ,z1=vd·t1·sinψ。
由系统误差引起的纵向飞行偏差Esx1和侧向飞行偏差Esz1可根据式(5)和式(6)计算获得。
Eφ,z1=vd·t1·sinEφ为发射航向角误差引起的侧向偏差。
因此,在0~t1内,由扇面发射角、各种误差和环境干扰导致的导弹飞行偏差为:
Ex1=Esx1·t1+Fxm·t1+vd·Δt;(14)
Ez1=Esz1·t1+Fzm·t1+Eψ,z1+Eφ,z1。(15)
式(14)、(15)中:Ex1、Ez1分别为无助推器情况下引入段导弹飞行纵向和侧向偏差。
引入段飞行终点散布后向边界端点位置为(Xj1_1L,Zj1_1L)和(Xj1_1L,-Zj1_1L),其中:
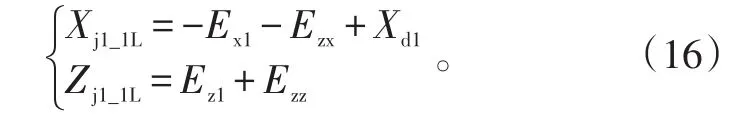
引入段飞行终点散布前向边界端点位置为(Xj1_1R,Zj1_1R)和(Xj1_1R,-Zj1_1R),其中:
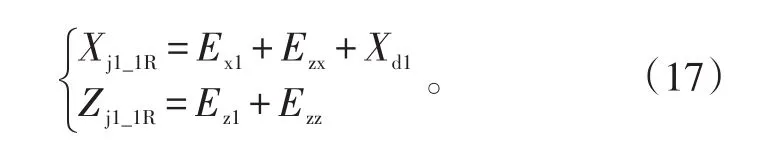
2.3 自控段飞行区域
导弹自控飞行区域是指导弹飞行t1至末制导雷达开机前可能飞过的区域。它与导弹的射程、雷达导引头作用距离、自控飞行时间、惯导精度等有关。
设Rd为导弹末制导雷达开机距离,Rm为导弹射击距离。导弹自控段飞行距离为Rzk=Rm-Rd-Xd1,飞行时间为t2=Rzk/vd。自控段飞行终点散布后向边界端点位置为(Xj2_1L,Zj2_1L)和(Xj2_1L,-Zj2_1L),其中:
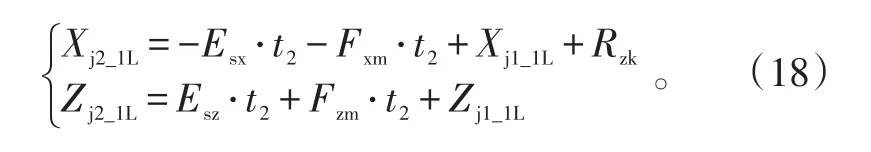
自控段飞行终点散布前向边界端点位置为(Xj2_1R,Zj2_1R)和(Xj2_1R,-Zj2_1R),其中:
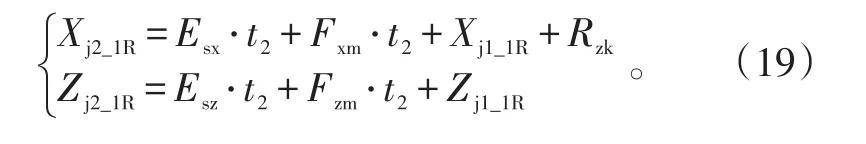
2.4 自导段飞行区域
自导飞行区域是指末制导雷达开机后导弹可能的飞行区域。与自控终点散布、末制导雷达开机距离、搜索范围、雷达波束宽度、目标位置等有关。
设φz1为导弹末制导雷达航向最大搜索角,φz2为导弹末制导雷达波束半宽,导弹自导段飞行时间t3=Rd/vd。由于此时导弹雷达已开机,导弹由自动控制改为自主导引,此时系统误差不再包含惯导误差,系统误差减为原来的1/2。
自导段飞行终点散布后向边界端点位置为(Xj3_1L,Zj3_1L)和(Xj3_1L,-Zj3_1L),其中:
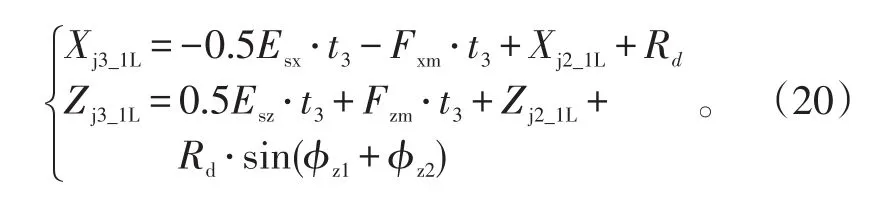
自导段飞行终点散布前向边界端点位置为(Xj3_1R,Zj3_1R)和(Xj3_1R,-Zj3_1R),其中:
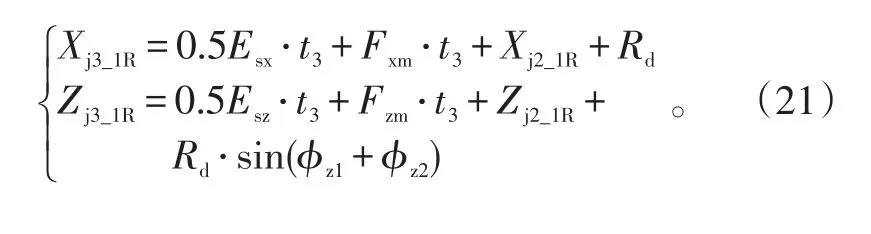
2.5 按最大飞行时间飞行区域
该段区域定义为弹上雷达开机后一直未搜索到目标,持续搜索直到导弹最大飞行时间,该区域应是自导段飞行区域的延续。
1)导弹最大飞行时间的计算。设vdmin为导弹最小平均速度;vmmax为目标最大速度。则导弹最大飞行时间的计算模型为
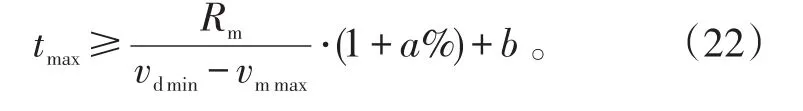
式(22)中:a%是考虑最大飞行时间的装订误差;b是为确保导弹完成装订射程飞行而设置的时间余量。
2)导弹按最大飞行时间飞行区域的计算。导弹按最大飞行时间飞行终点散布前向边界端点位置为(Xj_tmax,Zj_tmax)和(Xj_tmax,-Zj_tmax),其中:
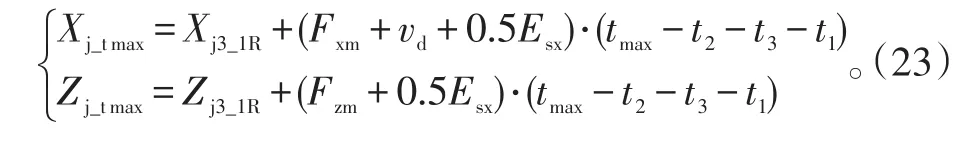
2.6 助推器落入区域
助推器落入区域是以助推器与导弹分离时导弹飞行高度、飞行速度和姿态角为初始参数,助推器作自由落体运动可能落入的区域。为简化起见,在此未考虑助推器所受的气动力。
将助推器视为质点,其坠落过程视为自由落体,影响助推器坠落区域的主要因素有:导弹飞行高度、飞行速度、偏航角、风速和风向等。其中偏航角是影响助推器侧向位移的主要因素,由于缺少弹道参数,因而以导弹与助推器分离时侧向位移最大点与发射点连线和射向的夹角作为助推器工作结束时导弹的最大偏航角,计算助推器脱落区域。即最大偏航角为
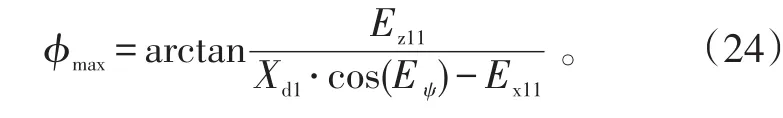
助推器分离时的起点散布后向边界端点位置为(Xj4_0L,Zj4_0L)和(Xj4_0L,-Zj4_0L),其中:
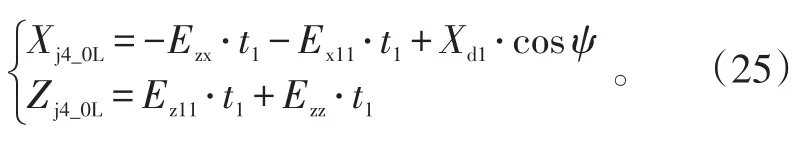
助推器分离时的起点散布前向边界端点位置为(Xj4_0R,Zj4_0R)和(Xj4_0R,-Zj4_0R),其中:
助推器分离后的运动是以初速即导弹速度vd进行的自由落体运动,则助推器坠落所需时间为:

式(27)中:Hzt为助推器分离时的导弹飞行高度,按导弹发射高度计算;g为重力加速度。
助推器坠落位置相对分离点最大值为:纵向最大偏差Xm=vd·t(取φmax=0时为最大),侧向最大偏差Zm=vd·t·sinφmax。
助推器坠落终点散布后向边界端点位置为(Xj4_1L,Zj4_1L)和(Xj4_1L,-Zj4_1L),其中:
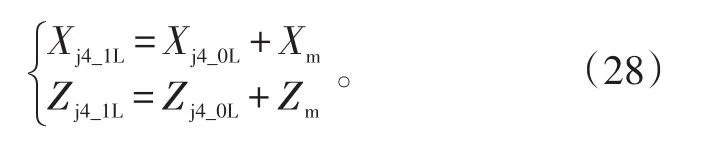
助推器坠落终点散布前向边界端点位置为(Xj4_1R,Zj4_1R)和(Xj4_1R,-Zj4_1R),其中:
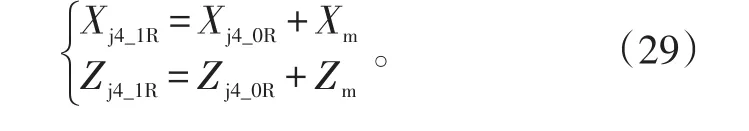
3 计算实例
假设导弹发射距离为32km,发射高度为5km。导弹正常飞行时的引入段、自控段、自导段、助推器脱落区域以及最大飞行时间飞行区域的划分见图3。
由以上计算实例可知,导弹飞行禁区各段区域不但存在交叉,而且包含了多个端点,这对演练保障人员扫海来说是非常困难的。出于简单实用的目的,需要对理论计算出来的区域进行数学处理,去掉大部分端点。处理原则是在涵盖上述各段区域的基础上,使禁区整体图形规则化、最小化。实用化的禁区处理效果图如图4所示。各端点坐标为:J1(-1.5,1.5),J2(24.840,10.088),J3(64.086,10.982),J4(-1.5,-1.5),J5(24.820,-10.088),J6(64.806,-10.982)。将各端点转换为经纬度,形成可实际应用的空舰导弹射击禁区。
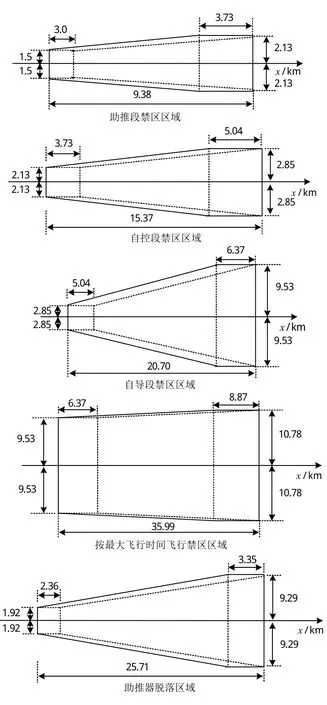
图3 射距32km、高度5km时的禁区各段计算结果Fig.3 Calculation of each phase in exclusion zone with32km-projection and5km-height
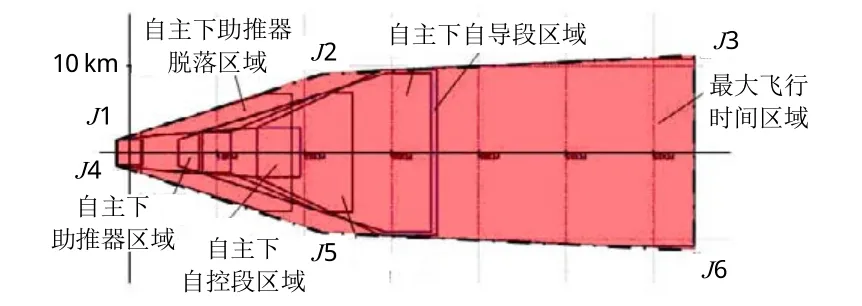
图4 实用禁区处理效果图Fig.4 Treatment effect drawing of practical forbidden zone
4 结论
本文在分析空舰导弹运动特性的基础上,建立了空舰导弹飞行禁区的计算模型并进行了实例计算,为得到简单实用的飞行禁区,对理论计算结果进行了处理。实用飞行禁区的确定可在保证安全的前提下,减少部队扫海作业量、缩短演训方案制定时间,对于提高部队战训水平具有较好的实用价值。
[1]龙飞,刘鼎臣,张林.航路规划技术对反舰导弹攻击影响的探讨[J].飞航导弹,2005(12):26-28. LONG FEI,LIU DINGCHEN,ZHANG LIN.Investigation of path planning effect on anti-ship missile attack ability[J].Aerodynamic Missile Journal,2005(12):26-28.(in Chinese)
[2]夏龙世,邹强,宋贵宝,等.舰艇摇荡对舰载导弹飞行参数影响的分析[J].海军航空工程学院学报,2005,20(2):223-226. XIA LONGSHI,ZOU QIANG,SONG GUIBAO,et al. Analysis of ship-rocking effect on flight parameters of ship-borne missiles[J].Journal of Naval Aeronautical Engineering Institute,2005,20(2):223-226.(in Chinese)
[3]冯铁城,朱文蔚.船舶的操纵与摇荡[M].北京:国防工业出版社,1989:71-150. FENG TIECHENG,ZHU WENWEI.Control and rock of ship[M].Beijing:National Defense Industry Press,1989:71-150.(in Chinese)
[4]赵晶,戴幻尧,来庆福,等.自控终点误差与目标散布下反舰导弹捕获概率分析[J].战术导弹技术,2010,31(2):64-68. ZHAO JING,DAI HUANYAO,LAI QINGFU,et al.Analysis of acquisition probability of anti-ship missile under auto-control termination error and target scattering[J].Tactical Missile Technology,2010,31(2):64-68.(in Chinese)
[5]周烨.反舰导弹航路规划的层次与任务[J].飞航导弹,2003(6):1-4. ZHOU YE.Level and task of anti-ship missiles path planning[J].Aerodynamic Missile Journal,2003(6):1-4.(in Chinese)
[6]赵建军,王光辉.反舰导弹自控终点误差散布及其改进[J].火力与指挥控制,2003,28(5):12-13. ZHAO JIANJUN,WANG GUANGHUI.The error spreading and improving of auto-control terminal point of antiship missiles[J].Fire Control&Command Control,2003,28(5):12-13.(in Chinese)
[7]沈如松,宋贵宝,周文松,等.导弹武器系统概论[M].北京:国防工业出版社,2010:65-66. SHEN RUSONG,SONG GUIBAO,ZHOU WENSONG,et al.Introduction of missile weapon system[M].Beijing:National Defense Industry Press,2010:65-66.(in Chinese)
Abstrract:The air-to-ship missile has a long range,and many interference factors impact its flight.It is very important for guiding our army's launch training and warfare application that determines the air-to ship missile forbidden combination zone.In this paper,based on analyzing the property of air-to-ship missile weapon system,main factors of affecting air-toship missile forbidden combination zone were generalized.Secondly,based on analyzing the movement property air-toship missile,the calculation model of forbidden and danger zone was built in use of particle flight trajectory simulation method and missile flight error combination method.
Calculation Mooddeell of Air-to-Ship Missile Forbidden Combination Zone
SHUAI Peng1,LIU Tie2a,WEN Jian-guo2b
(1.Naval Equipment Department,Beijing 100071,China; 2.Naval Aeronautical and Astronautical University a.Department of Airborne Vehicle Engineering; b.Department of Scientific Research,Yantai Shandong 264001,China)
air-to-ship missile;forbidden combination zone;calculation model
TJ762.2+4
A
1673-1522(2014)01-0062-05
10.7682/j.issn.1673-1522.2014.01.014
2013-11-10;
2013-12-10
帅鹏(1979-),男,工程师,硕士。
