单跨斜支承梁内力的影响因素分析

柯赛华，吴 晟，宁建根，谢 群，张戎令

（1.江西赣北公路勘察设计院，江西 九江 332700；2.兰州交通大学土木学院，甘肃 兰州 730070）

0 引言

近年来随着高等级公路、城市道路和立交枢纽的快速发展，因受地形地貌、设计净空、设计线形等的约束，斜弯桥结构得以广泛的应用[3]。斜梁桥的大量出现，引起了工程界的高度重视。20世纪90年代后，国内专门成立了“斜弯梁桥”课题组，并取得了一定的研究成果。但是，斜弯梁桥的研究远不如常规桥梁那样彻底、完善、系统。

由于弯扭耦合作用，单跨斜支承梁在左右梁内有较大扭矩产生，其结构表现为一次超静定结构，且内力分布及其规律与常规梁桥有很大不同。《混凝土斜梁桥》一书提出了考虑支承刚度的ESS（弹性斜支承梁）分析模式，并对单跨斜支承梁的影响因素进行了分析，提出了多项研究结论，其中第四点中提出：当端横梁刚度满足id＜i/5时，单跨斜梁可按简支梁（著作中简支梁为常规桥梁，非RSS模式桥梁）计算。本文在分析支承刚度对单跨斜支承梁（RS型）的影响中，考虑不同斜度和弯扭刚度比的影响，引入线刚度比概念，更加全面地分析了单跨斜支承梁内力的影响因素。

1 理论分析

本文以沪宁高速公路20m单跨斜梁桥为例，具体数据如下：

主梁：计算跨径l=18.66m。

斜度： φ1,2=60°，I=0.0869m4,J=0.0134m4。

弯扭刚度比：κ=15.121。

40＃混凝土弹性模量：E=3.3×107kPa（共六片梁）。

端横梁： Id=0.04768m4，ld=2.1/cos60°(m)。

圆形橡胶支座：Dr=300mm，tr=52mm，t0=5mm，Er=7.532×105kPa。

下面结合实例，分析支承刚度在均布荷载作用下对主梁内力的影响，并在ESS计算模式下推导该单跨斜支承梁桥效应计算公式。

1.1 支承刚度分析

将支座和端横梁视作弹性支承连续梁，用该模型替代非刚性的边界条件，分析端横梁单刚矩阵和橡胶支座的竖向刚度矩阵，建立支承刚度矩阵[Ksupport]=。按位移法求解端横梁抗扭刚度，按照力学方法求解竖向支承刚度。实际工程中，一般只考虑端横梁的两孔连续梁的作用即可求出相应的解，并且满足精度要求。

分析结果如下：

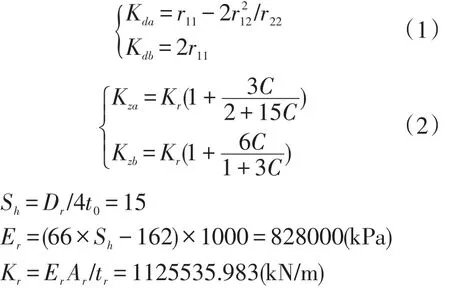
式中：

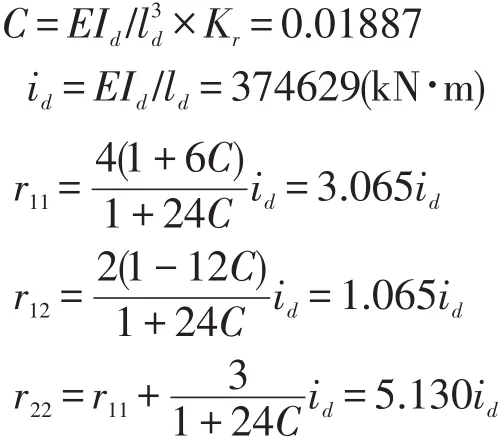
求得A、B端的抗扭刚度和竖向支承刚度：

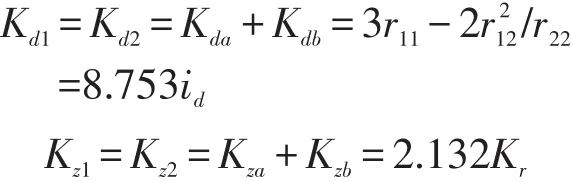
1.2 基本结构分析

解除B端抗扭约束，建立静定的基本结构，在T2作用下，利用力学平衡条件[1-2]，得到：

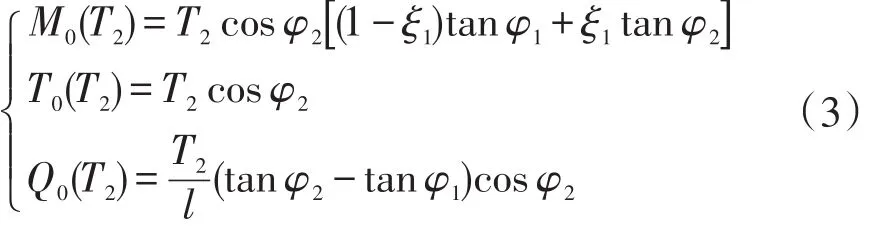
1.3 ESS分析

对于ESS图式而言，T2处无相对转动，利用力法，建立效应方程；由虚功原理求得均布荷载作用下T2的数值。最后，组合均布作用下基本结构的内力，得到均布荷载作用下的效应[2]：

反力：

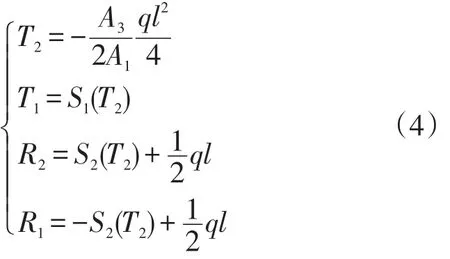
内力：

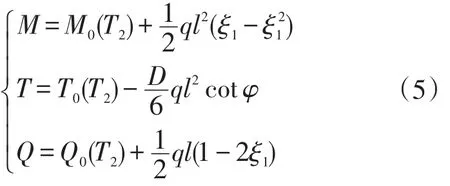
式中：

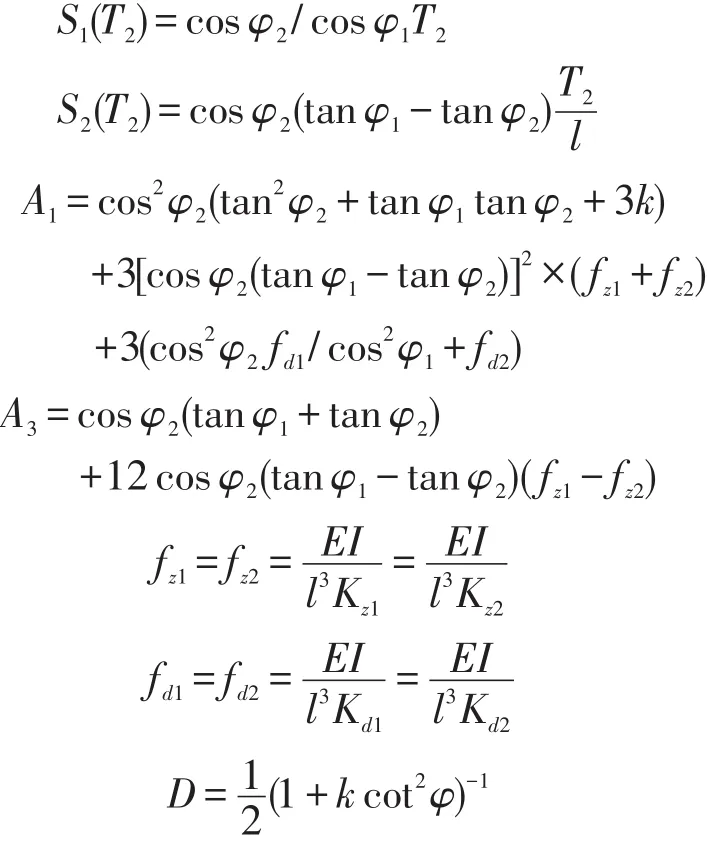
2 不同斜度和支承刚度对斜支承梁的影响

《混凝土斜梁桥》一书仅分析了同一斜度和弯扭刚度比下，支承刚度的关系图。本文将分析不同斜度和弯扭刚度比的支承刚度关系图。由于本文分析的是RS型单跨斜支承梁桥（φ1=φ2），所以可以将所用公式进行简化，然后进行对比分析。

2.1 不同斜度和弯扭刚度比的支承刚度关系

倘若仅讨论端横梁的设置，则不能全面反映单跨斜支承梁的内力变化规律，因为某个端横梁的线刚度也是斜度的函数。在斜度和端横梁惯性矩同时进行线性变换中，可以发现idi（线刚度比，用η表示）变化跟弯扭刚度比没有关系，并且符合一定规律，将这个规律拟合成曲线函数，如图1所示。

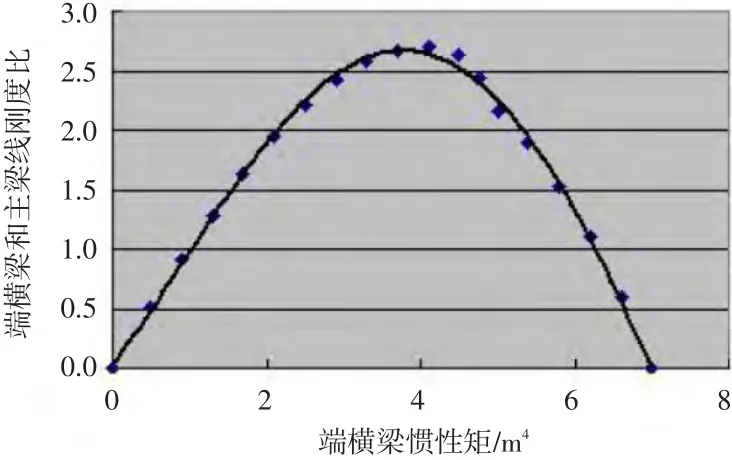
图1 端横梁和主梁线刚度比曲线

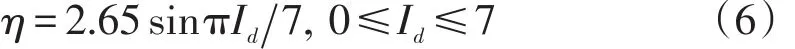
分析式（6）可知，随着斜度和端横梁惯性矩的增加，线刚度比η不是简单地递增。

由于端横梁惯性矩过大和过小都没有工程实际意义，故本文只分析1.5≤Id≤6时，线刚度比η和弯扭刚度比k对单跨支承梁的内力影响。

在弯扭刚度比k分别为15.121、10、5、1的情况下，当1.5≤Id≤6时，对比分析线刚度比η对跨中弯矩M12和扭矩T2的影响情况。

整理分析数据并绘制成图，如图2和图3所示。

根据上述曲线特征，拟合的曲线函数为：

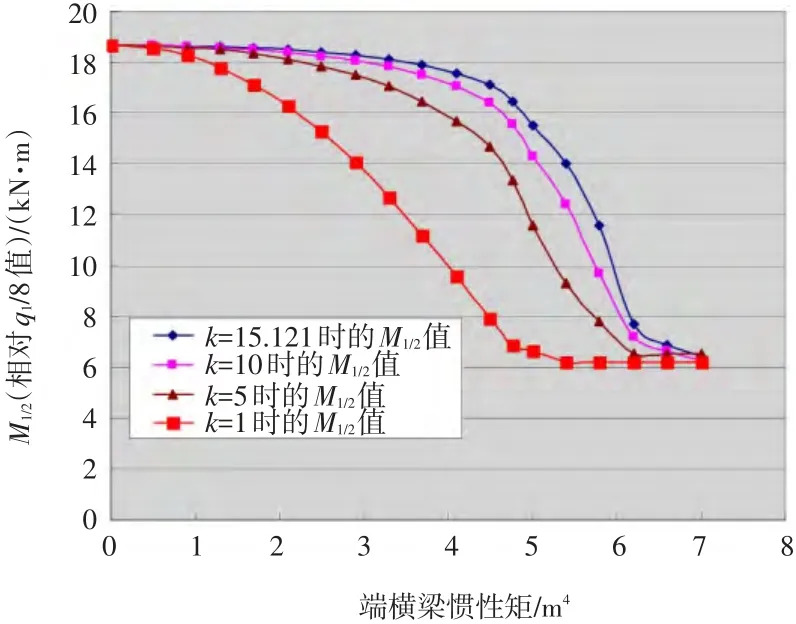
图2 不同线刚度比和弯扭刚度比的跨中弯矩

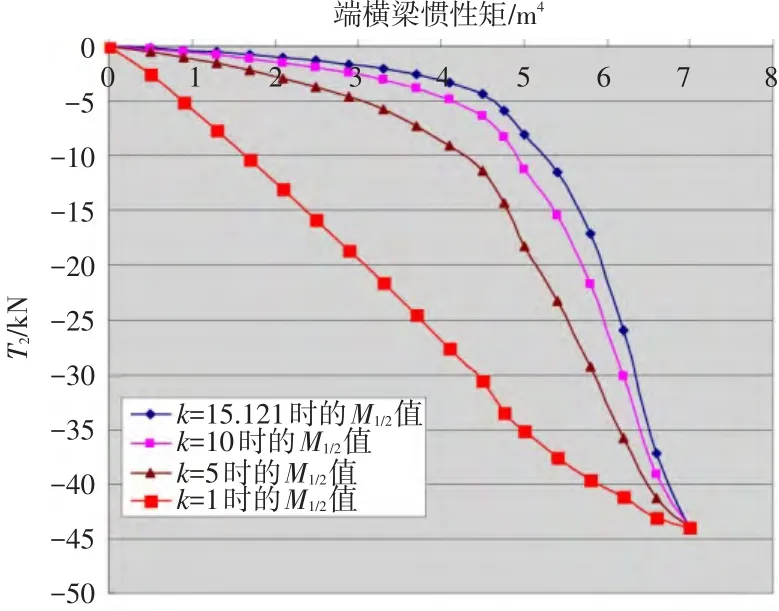
图3 不同线刚度比和弯扭刚度比的右端扭矩

2.2 关系图对比分析

在1.0≤Id≤6区间内，线刚度比η可以分为两个取值区间：1.0≤Ida≤3.5区间内，ηa∈[1.35,2.65]；3.5≤Idb≤6.0区间内，ηb∈[2.65,1.35]。其 中 ， 3.5≤Idb≤6.0表示线刚度比b区间取值是逐渐减小的区间。

2.2.1 1.0≤Ida≤3.5,ηa∈[1.35,2.65]区间内

（1）在该区间内，从以上图2、图3中可以看出，当Id→0时，M12、T2均趋向于简支梁计算结果，与斜度无关。

（2）在该区间内，当弯扭刚度比k变小时，随着ηa的增大，M12、T2的折减率加大。内力折减率见表1，弯矩减幅幅度比扭矩增幅变化较慢。

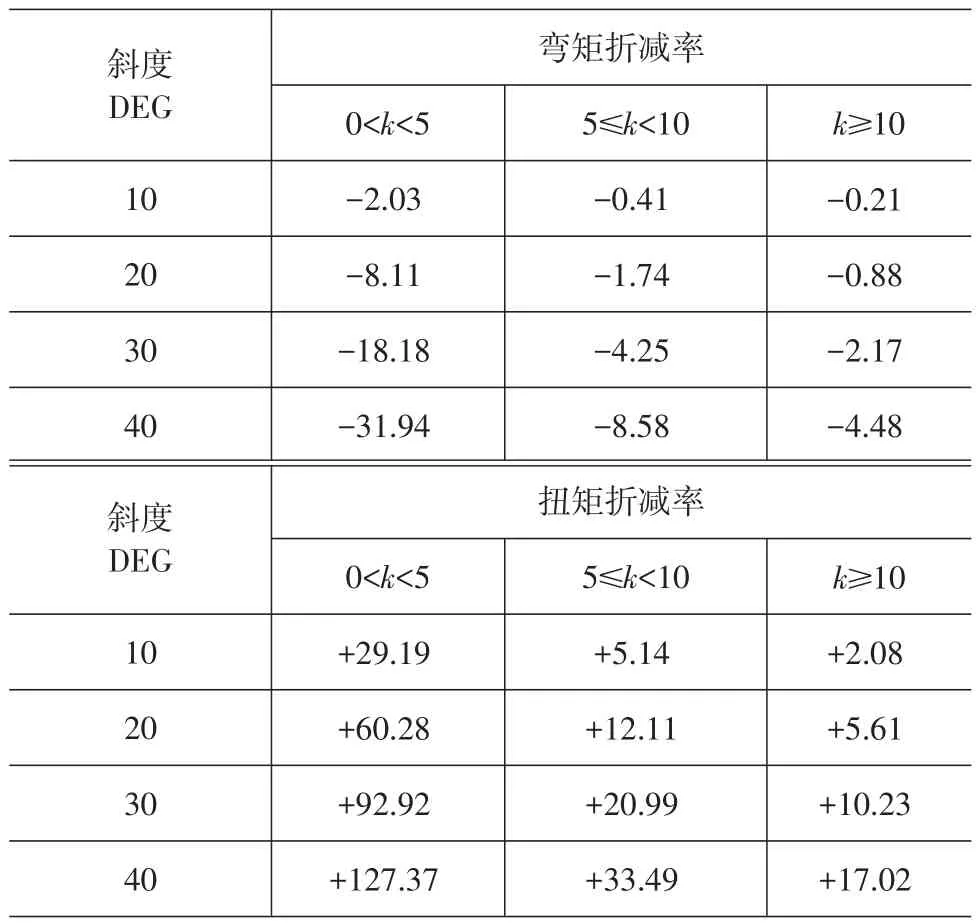
表1 内力折减率

当满足下列情况时，可看作简支梁计算M12：

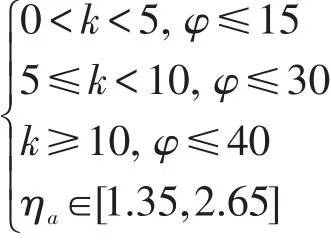
当满足下列情况时，T2数值较小，可以不计：

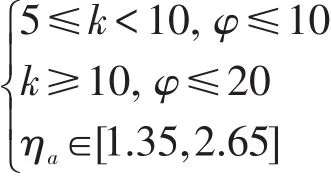
（3）在该区间内，弯扭刚度比k对内力的影响比较显著。

2.2.2 3.5≤Idb≤6.0,ηb∈[2.65,1.35]区间内

（1）在该区间内，从以上图2、图3可以看出，当Id→∞时，M12、T2均趋向于固端梁计算结果。

（2）在该区间内，虽然斜度继续增加，但是线刚度比ηb在逐渐减小，回归到与ηa对称状态，M12、T2发生了急剧变化。内力折减率见表2。

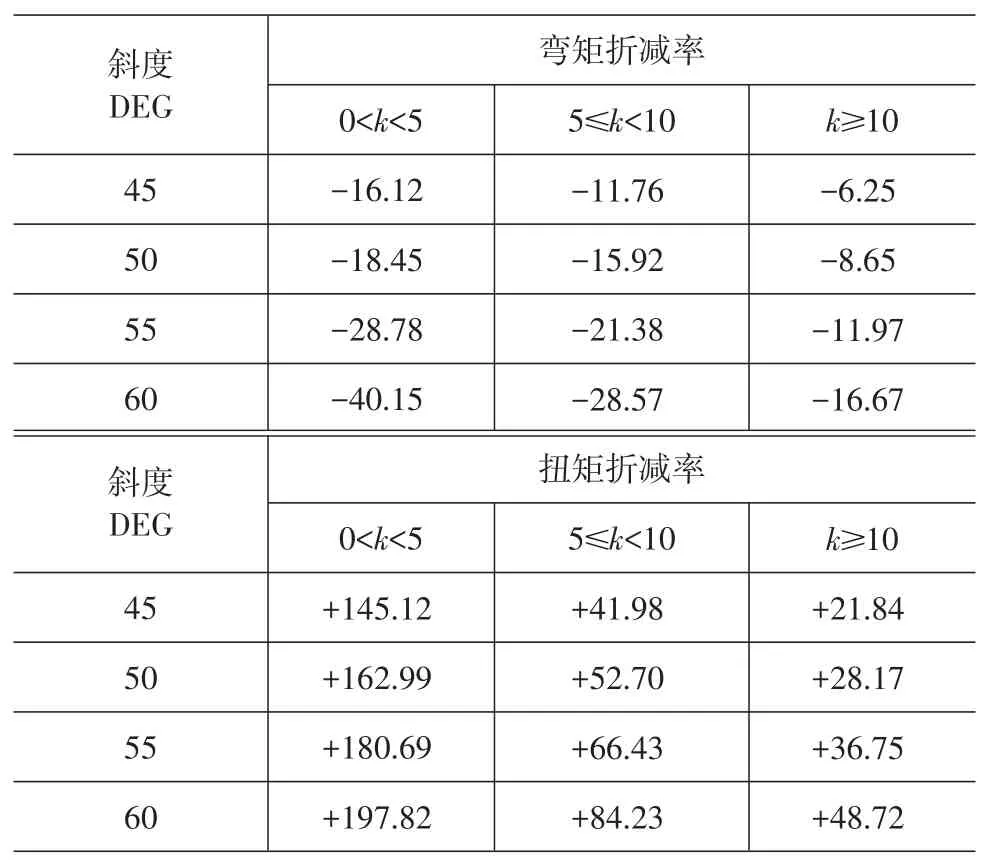
表2 内力折减率（正号增加，负号减少）

在ηb∈[2.65,1.35]区间内，由表2可知， M12随着斜度和弯扭刚度比的变化，按照5%～12%的增长率在急剧减少。跨中弯矩折减率最大值为-40.15。T2急剧变化，减小更加明显。研究和设计过程中，必须认真计算T2的值。

（3）在该区间内，弯扭刚度比k对内力的影响特别显著。

3 结论

（1）RS型单跨斜支承梁的内力变化受Kz影响较小，可以忽略不计。

（2）由于线刚度是斜度的函数，当斜度和端横梁惯性矩同时线性变化时，可以得知线刚度比η的变化符合一定规律。本文简单地将其回归为η=2.65sinπId7(0≤Id≤7)。

（3）RS型单跨斜支承梁设计和计算中，如将M12作为控制指标，当满足下列条件时，弯矩可按照简支梁进行处理：

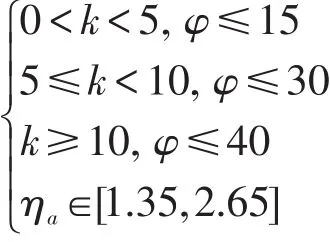
如将T2作为控制指标，当满足下列条件时，可按照简支梁进行处理，否则要准确计算T2：

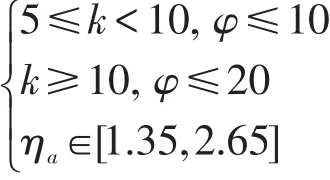
（4）在 ηb∈[2.65,1.35]区间内， M12、T2急剧变化，特别是端横梁惯性矩在4.5≤Id≤5.5范围，斜度大于45°时，须认真加以分析计算。

（5）在线刚度比η的两个取值区间内，弯扭刚度比k对单跨斜支承梁内力的影响都较大，且k值越小，影响越显著。箱梁k值一般较小，设计和计算时要引起足够的重视。

[1] 夏淦.斜梁结构分析[M].北京：人民交通出版社，1994.

[2] 黄平明.混凝土斜梁桥[M].北京：人民交通出版社，1999.

[3] 邵容光.混凝土弯梁桥[M].北京：人民交通出版社，1994.

[4] 柯赛华.斜交梁桥受力特性及设计研究[J].交通标准化，2012，（18）：47-52

[5] 龙驭球.结构力学教程[M].北京：高等教育出版社，2001.