有限元方法(FEM)求解奇异摄动Volterra积分微分方程
2014-07-06万正苏徐邦启
陶 霞, 万正苏, 徐邦启, 章 敏
(湖南理工学院 数学学院, 湖南 岳阳 414006)
有限元方法(FEM)求解奇异摄动Volterra积分微分方程
陶 霞, 万正苏, 徐邦启, 章 敏
(湖南理工学院 数学学院, 湖南 岳阳 414006)
运用有限元方法(FEM)求解奇异摄动Volterra积分微分方程. 数值算例表明, 在局部加密网格下, FEM解具有高精度性质.
奇异摄动Volterra积分微分方程; 局部加密网格; 有限元方法
引言
考虑如下奇异摄动Volterra积分微分方程:
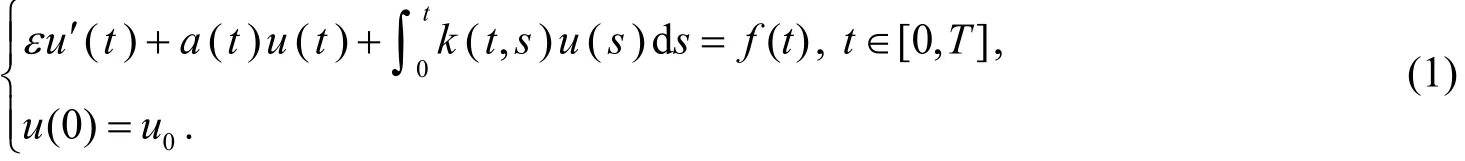
其中0<ε≪1为小参数, 0<α≤a(t),f(t)和k(t,s)充分光滑.
奇异摄动积分微分方程广泛存在于实际工程计算中, 如流体力学、天体力学、量子力学、光学、化学、生物学以及控制论等领域中. 本文讨论的奇异摄动Volterra积分微分方程来源于许多物理和生物问题, 如扩散耗散过程、流行病动力学、同期控制系统、更新过程和拉伸纤维等[3~9]. 奇异摄动Volterra积分微分方程理论综述见文[1]. 由于小参数的存在, 解在很薄的边界层中变化非常剧烈, 数值模拟解的急剧变化异常困难. 另一方面, 为准确描述这类问题, 必须考虑系统对于过去经历的记忆效应. 因此, 寻找求解奇异摄动Volterra积分微分方程的高精度数值方法尤其困难.
关于数值求解奇异摄动Volterra积分微分方程已有一些研究工作, 如指数型有限差分方法、差分方法、隐Runge-Kutta方法以及张力样条配置方法等[2]. 采用LDG-CFEM耦合方法求解奇异摄动Volterra积分微分方程, 在Shishkin网格下, 耦合解具有高精度性质. 本文运用有限元方法(FEM)求解这类方程, 算例结果表明: FEM解同样具有高精度性质. 而且在局部加密网格下, 在节点处FEM解具有2p阶的超收敛性.
1 有限元方法(FEM)
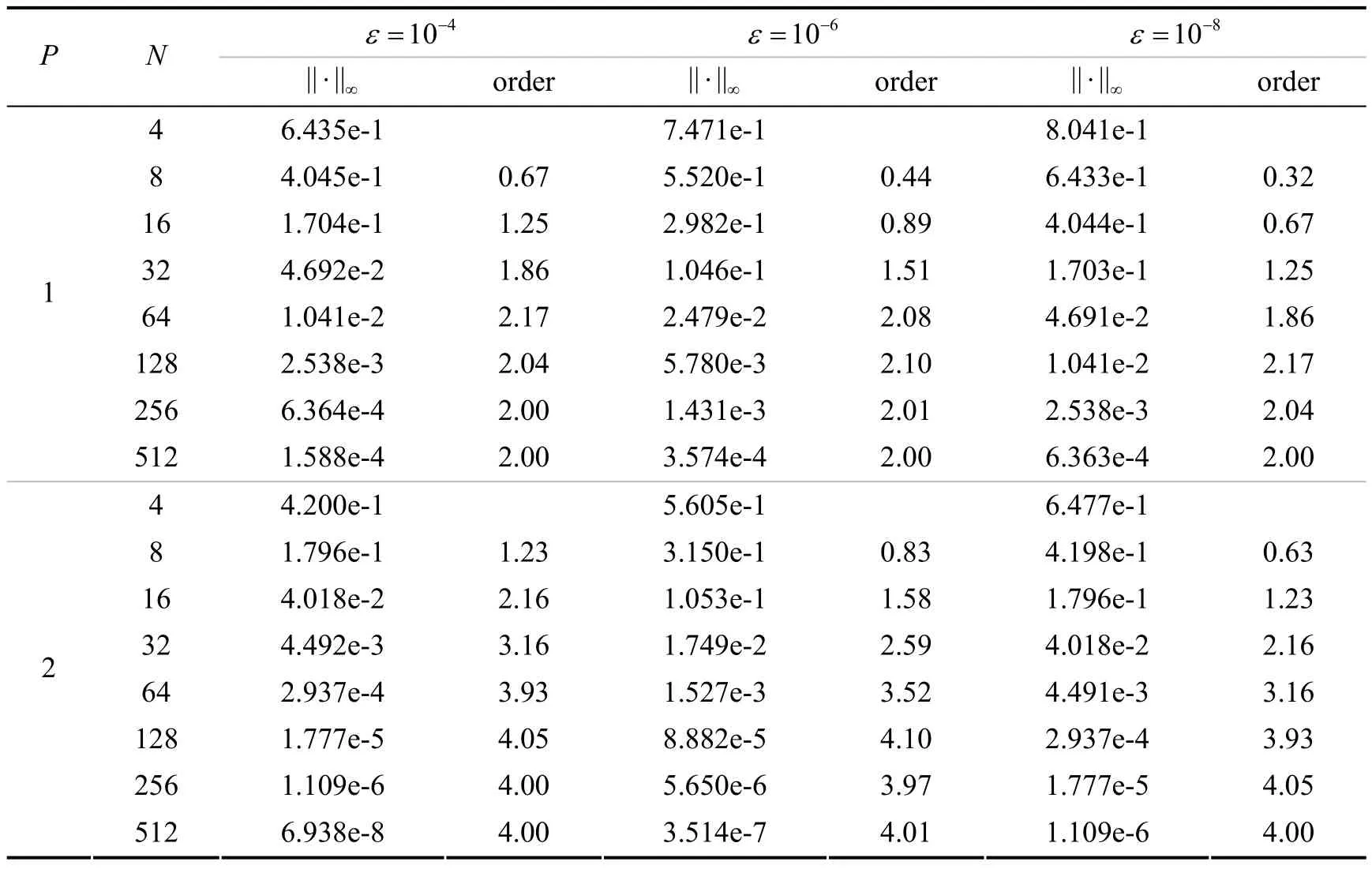
首先将区间[0,T]剖分, 剖分节点为0=t0 其中p≥1,q≥1. 在区间[0,T]上, 运用有限元方法(FEM), 即寻找使得 考虑奇异摄动Volterra积分微分方程(1), 其中a=1,k(t,s)=exp(s), 初值为u(0)=1+exp(−1),对应的真解为u(t)=exp(t−1)+exp(−(1+ε)t/ε).并且其真解在t=0附近出现边界层现象, 边界层厚度为O(ε). 这里取τ=min(0.5,−ε(p+1)logε). 当小参数ε分别取10−4、10−6和10−8时, 表1给出了相应的最大模误差和收敛阶. 表1中数据结果表明: 将区间[0,τ]和[τ,1]分别均匀剖分后, FEM解不仅稳定, 而且精度高.可以观察到: 在节点处的FEM解具有2p阶的超收敛性. 图1和图2分别显示了在线性元和二次元情形下的有限元解在节点处的误差图. 为了研究FEM解的超收敛性, 图3~图6给出了区间[0,τ]和[τ,1]上FEM解的误差图. 当ε=10−8时, 将[0,1]进行512剖分后, 图3和图4分别显示了边界层[0,τ]的前三个单元上运用FEM方法在线性元和二次元情形下的误差图; 图5和图6分别显示了[τ,1]最后三个单元上运用FEM方法在线性元和二次元情形下的误差图. 表1 FEM方法([0, 1]) 图1 FEM方法,P= 1 图2 FEM方法,P= 2 图3 FEM方法,ε= 10-8,P= 1 图4 FEM方法,ε=10-8,P= 2 图5 FEM方法,ε= 10-8,P= 1 图6 FEM方法,ε= 10-8,P= 2 [1] J. P. Kauthen.A survey of singularly perturbed Volterra equations[J]. Appl. Numer. Math., 1997, 24: 95~114 [2] 陶 霞, 章 敏, 徐邦启. 求解奇异摄动Volterra积分微分方程的LDG-CFEM耦合方法[J]. 湖南理工学报(自然科学版), 2014, 27: 12~15 [3] J. S. Angell and W. E. Olmstead.Singularly perturbed Volterra integral equations[J]. SIAM J. Numer. Math., 1987, 47: 1~14 [4] J. S. Angell and W. E. Olmstead.Singularly perturbed Volterra integral equationsⅡ[J]. SIAM J. Numer. Math., 1987, 47: 1150~1162 [5] A. M. Bijura.Rigorous results on the asymptotic solutions of singularly perturbed nonlinear Volterra integral equations[J]. J. Integ. Equat. Appl., 2002, 14: 119~149 [6] A. M. Bijura.Asymptotics of integrodifferential models with integrable kernels[J]. Int. J. Math. Sci., 2003, 25: 1577~1598 [7] G. S. Jordan.A nonlinear singularly perturbed Volterra integrodifferential equation of nonconvolution type[J]. Proc. Roy. Soc. Edinburgh Sect. A. 80, 1978: 235~247 [8] G. S. Jordan.Some nonlinear singularly perturbed Volterra integro-differential equations[J]. in: Volterra Equations(Proc. Helsinki Sympos. Integral Equations, Otaniemi, 1978). Lecture Notes in Mathematics, Vol. 737, Springer, Berlin, 1979:107~119 [9] A. S. Lodge, J. B. Mcleod and J. E. Nohel.A nonlinear singularly perturbed Volterra integrodifferential equation occurring in polymer rheology[J]. Proc. Roy. Soc. Edinburgh Sect. A. 80, 1978: 99~137 Finite Element Method (FEM)for Solving Singularly Perturbed Volterra Integrodifferential Equations TAO Xia, WAN Zheng-su, XU Bang-qi, ZHANG Min This paper implements finite element method (FEM) for solving singularly perturbed Volterra integrodifferential equations. Numerical results show that FEM solution has high accuracy property under layer-adapted mesh. singulary perturbed Volterra integrodifferential equations; layer-adapted mesh; finite element method (FEM) O241.82 A 1672-5298(2014)03-0023-03 2014-07-18 国家自然科学基金项目(11371074); 湖南省教育厅一般项目(13C366); 湖南理工学院校级科研项目(2013Y11) 陶 霞(1982 − ), 女, 湖南湘阴人, 博士, 湖南理工学院数学学院讲师. 主要研究方向: 微分方程数值解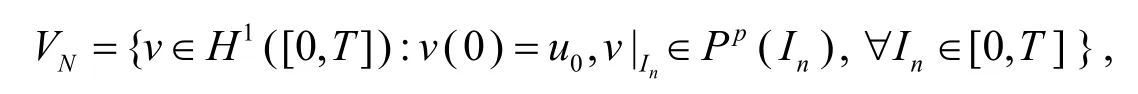

2 数值算例






(College of Mathematics, Hunan Institute of Science and Technology, Yueyang 414006, China)
