一元八次方程的矩阵解法及其推广
2014-07-06万正苏沈红玉潘婷婷
万正苏, 李 英, 沈红玉, 谢 磊, 潘婷婷
(1. 湖南理工学院 数学学院, 湖南 岳阳 414006;2. 临湘市第五中学, 湖南 临湘 414300)
一元八次方程的矩阵解法及其推广
万正苏1, 李 英1, 沈红玉2, 谢 磊2, 潘婷婷1
(1. 湖南理工学院 数学学院, 湖南 岳阳 414006;2. 临湘市第五中学, 湖南 临湘 414300)
利用矩阵的特征值和特征向量以及实对称矩阵的相似和合同理论, 给出了几类特殊一元八次方程的矩阵解法,并将其推广到一般的一元高次方程.
实对称矩阵; 相似; 合同; 八次方程
引言
自然科学和社会科学中的很多问题都可用代数方程或微分积分方程来进行描述, 而且微分积分方程的数值解以及部分微分积分方程的精确解最后都归结为代数方程(组)的求解, 因此研究代数方程的求解对数学理论的发展以及在科学工程的实际计算方程中都是有重要意义和价值的. 代数方程的求解问题也一直是数学界的一个热点问题, 这方面的研究成果数不胜数. 二、三、四次方程根的表达式以及根与系数之间的关系都已经很成熟, 但求五次及更高次方程的根式解法, 数学家们经历了一个非常艰难的过程. 第一个证明“高于四次方程不能用根号求解”的是挪威数学家阿贝尔. 也就是说, 对于一般的高于五次的方程没有一般的根式解法.
文[1]提出了求解一元实系数四次方程的矩阵解法, 文[2]研究了三类特殊实系数一元六次方程的矩阵解法. 受文[1]的思想的启发, 本文利用矩阵的特征值和特征向量以及实对称矩阵的相似和合同理论, 给出几类特殊一元八次方程的矩阵解法, 并将其推广到一般的一元高次方程.
1 实系数八次方程的矩阵解法
一元实系数八次方程的一般形式为
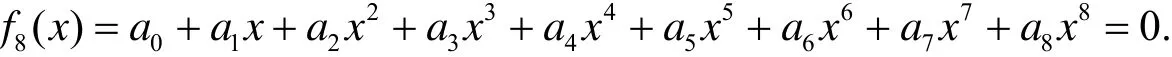
若记
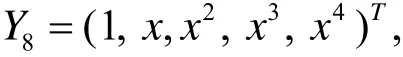
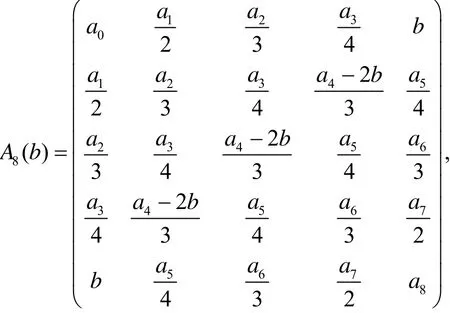
注意det(A8(b))=0是一个关于b的五次实系数方程, 由代数基本定理知一元n次实系数方程在复数域内有n个根, 且虚数根是成对出现, 因此至少存在一个实数b*, 使得det(A8(b*))=0. 若存在det(A8(b))=0的一个实根b*使得A8(b*)的惯性指数小于等于2 (或A8(b*)的秩R(A8(b*))≤2), 而A8(b*)是实对称矩阵, 则一定存在可逆矩阵或正交矩阵Q8使得其中
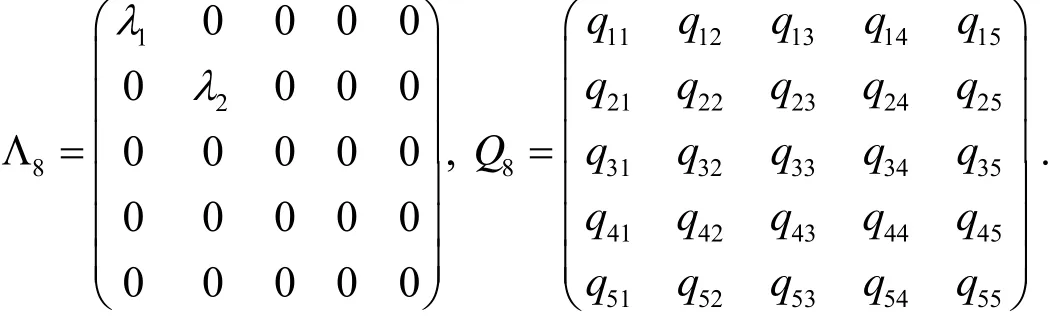
记
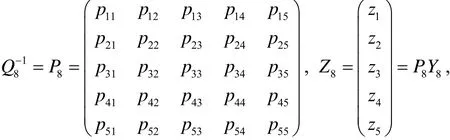
则有
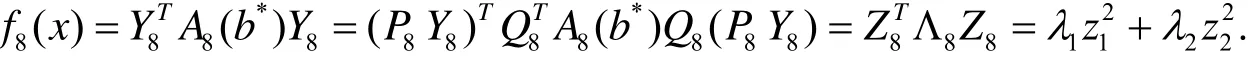
(ⅰ) 当λ1, λ2同号时, 不妨设λ1>0,λ2>0, 则有
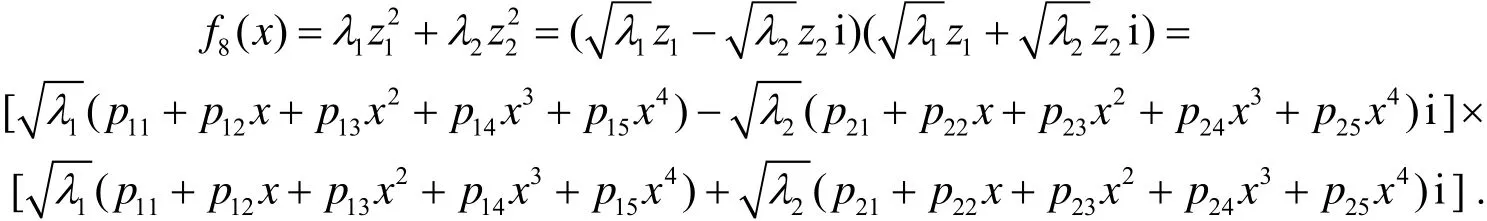
于是八次方程f8(x)=0的求解等价于求如下两个四次方程的根
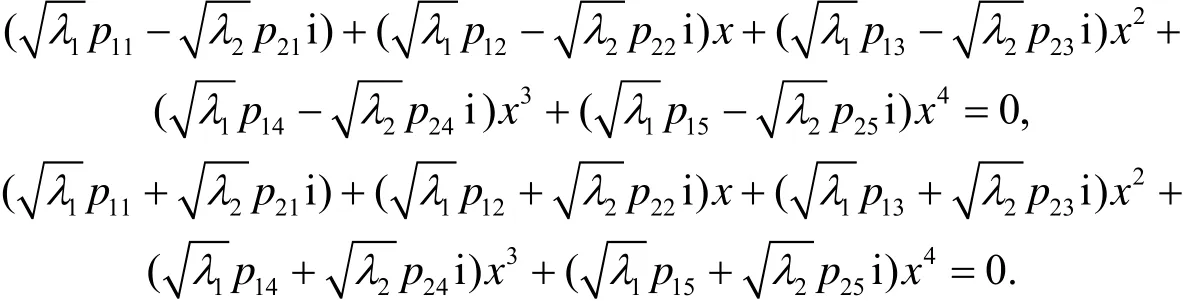
(ⅱ) 当λ1, λ2异号时, 不妨设λ1>0,λ2<0, 则有
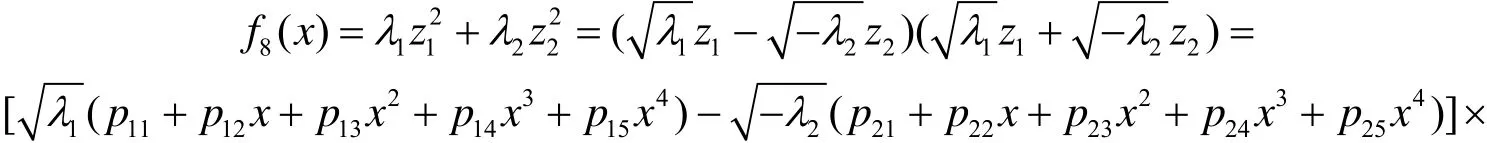
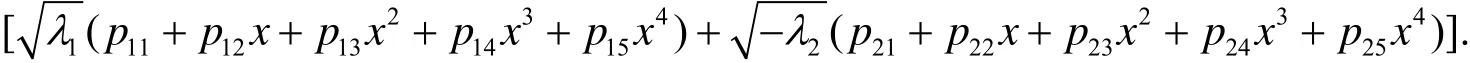
于是八次方程f8(x)=0的求解等价于求如下两个四次方程的根:
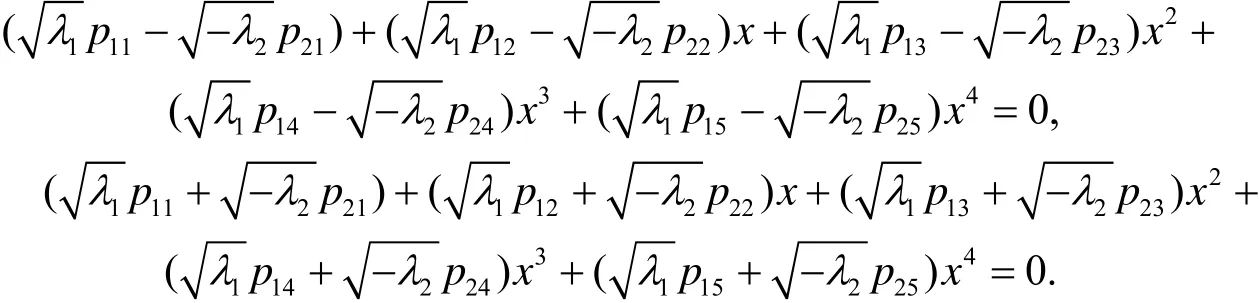
(ⅲ) 当λ1, λ2中有一个为零时, 不妨设λ2=0, 则有
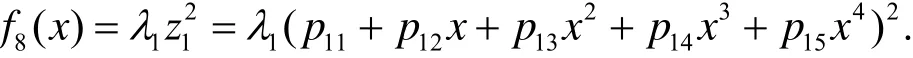
于是八次方程f8(x)=0的求解等价于求如下四次方程的根:
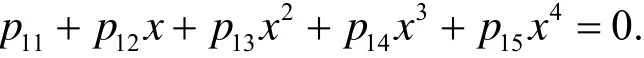
注当a8=0,a7≠0时, 上面的方法就是实系数一元七次方程的矩阵解法.
例1 解方程1+2x+3x2+4x3+5x4+4x5+3x6+2x7+x8=0.
解按上述方法求解可得
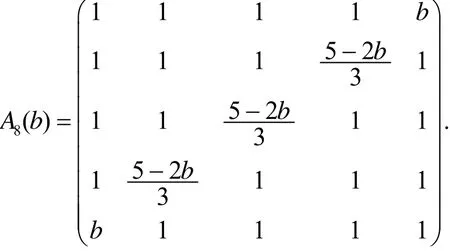
取det(A8(b))=0的实数根b*=1, 对Q8(1)进行合同变换可得其中
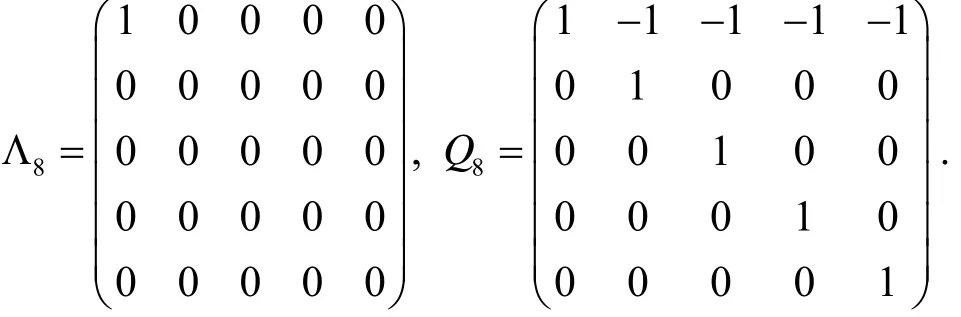
易得

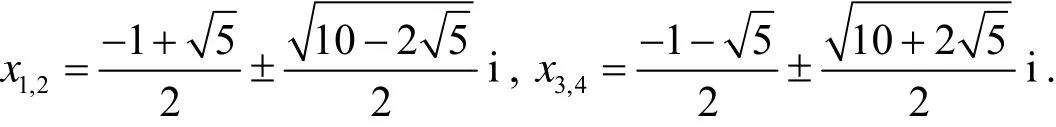
2 实系数2n次方程的矩阵解法
一元实系数2n次方程的一般形式如下

若记
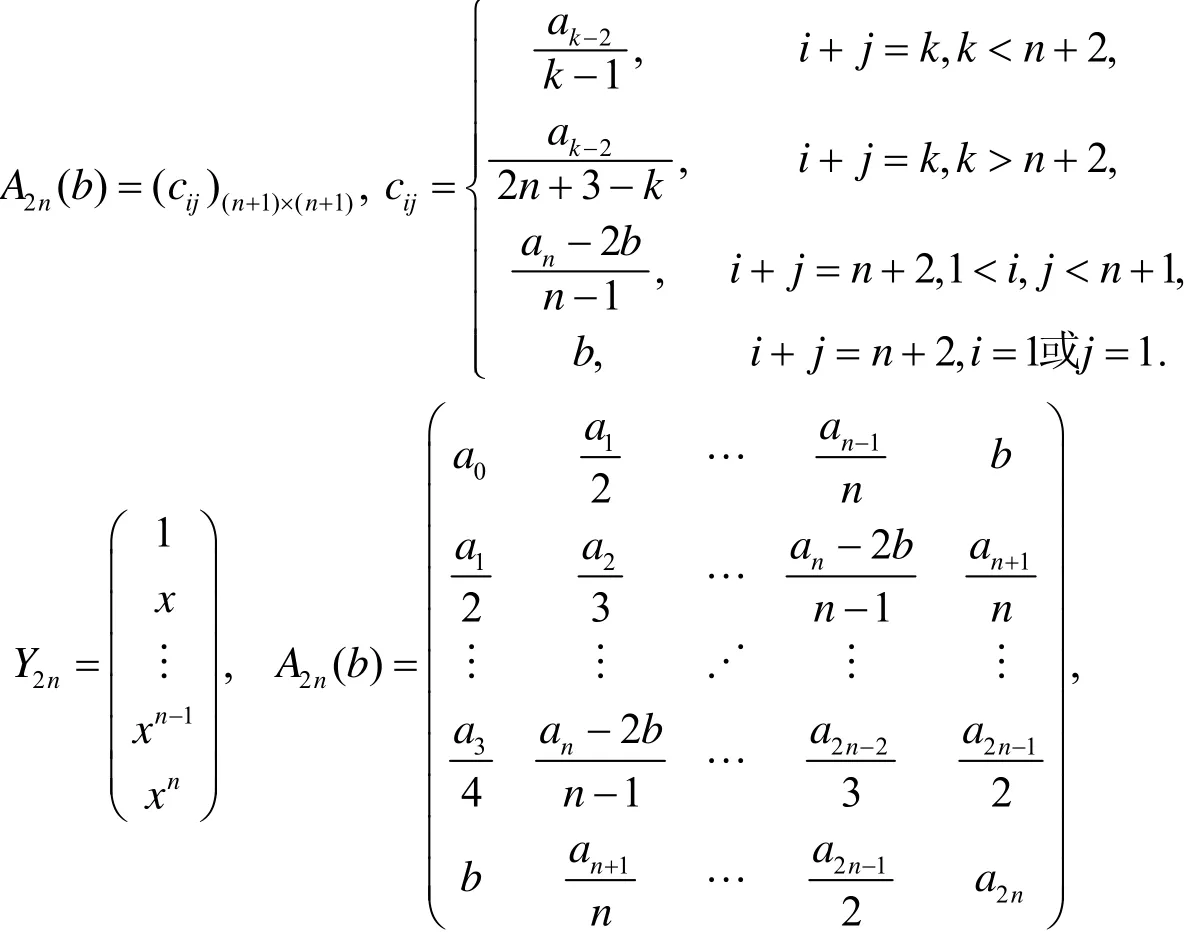
则有
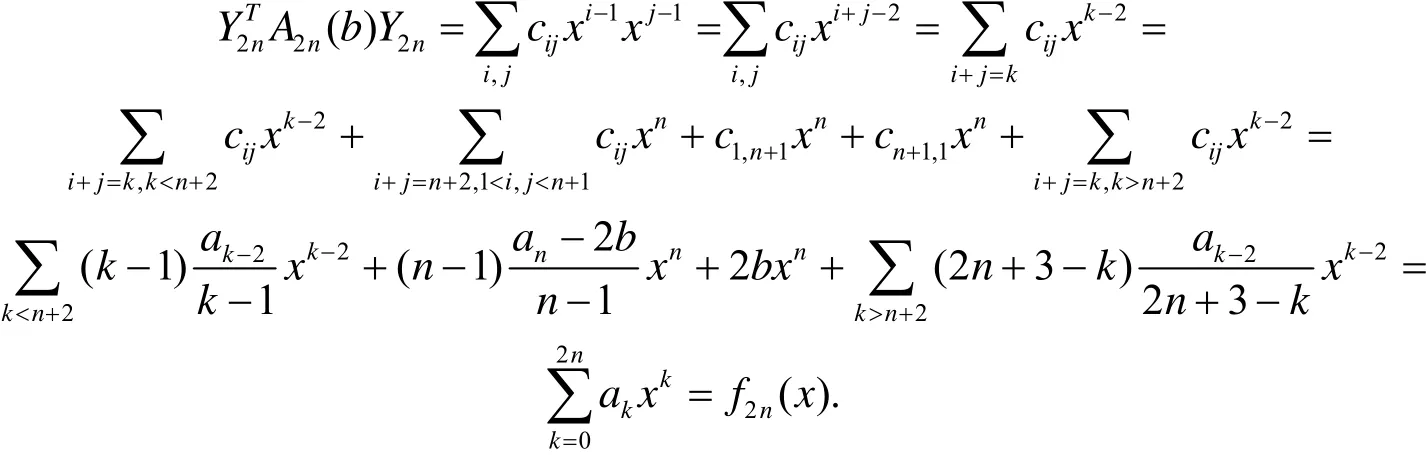
det(A2n(b))=0是一个关于b的2n次实系数方程. 若存在det(A8(b))=0的一个实根b*, 使得A2n(b*)的惯性指数小于等于2 (或A2n(b*)的秩r(A2n(b*))≤2), 而A2n(b*)是实对称矩阵, 则一定存在可逆矩阵或正交矩阵Q2n使得其中

记

则有
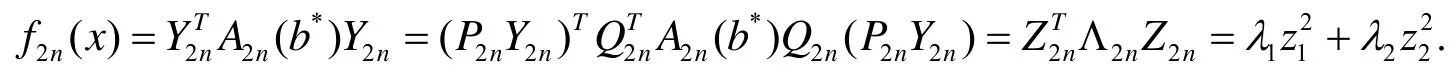
(ⅰ) 当λ1, λ2同号时, 不妨设λ1>0,λ2>0, 则有
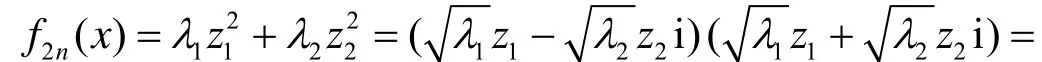
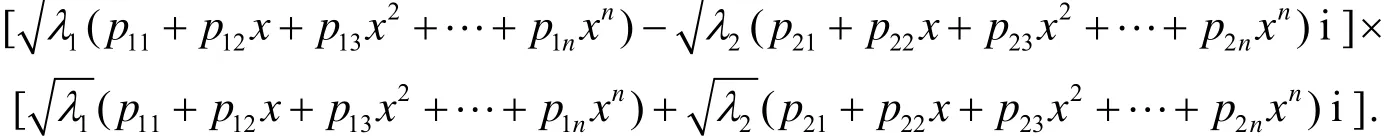
于是原2n次方程2()0
n fx=的求解等价于求如下两个四次方程的根

(ⅱ) 当1,2λ λ异号时, 不妨设10,20 λ>λ<, 则有
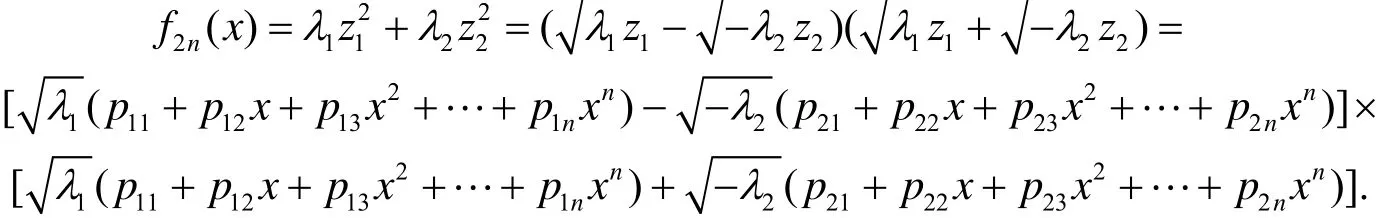
于是原2n次方程的求解等价于求如下两个四次方程的根
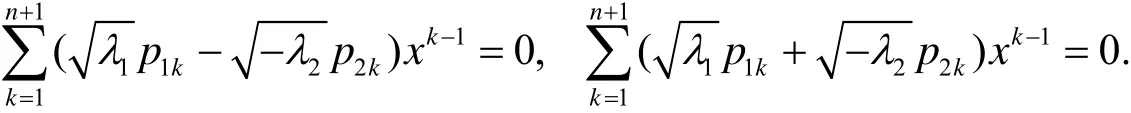
(ⅲ) 当1,2λ λ中有一个为零时, 不妨设λ2=0, 则有
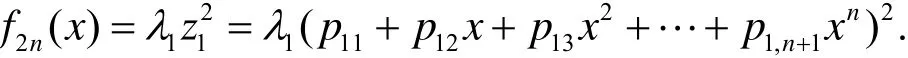
于是原八次方程f8(x)=0的求解等价于求如下四次方程的根
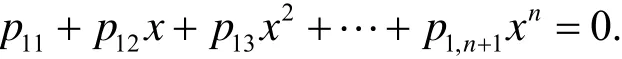
3 结束语
本文所提出的高次方程的矩阵解法的第一步是将方程所对应的多项式转化为二次型, 在该二次型的矩阵中引入了一个自由参数, 实际上我们可以引入多个自由参数. 比如第1小节所讨论的八次方程可记为
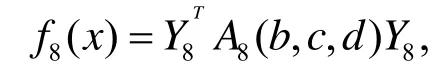
其中
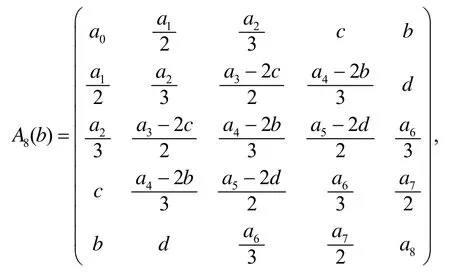
b,c,d为任意实数. 随着自由参数的增加, 本文所讨论的方法的适用范围将扩大, 但这还有待进一步的研究.
[1] 盛兴平. 实系数一元四次方程的矩阵解法[J]. 数学通报, 2002, 12: 37~37
[2] 范 军, 孔志宏. 三类特殊的实系数一元六次方程的矩阵解法[J]. 高等数学研究, 2009, 12(4): 66~69
Matrix Methods for Solving Unitary Equation of The Eighth Degree and It's Generalization
WAN Zheng-su1, LI Ying1, SHEN Hong-yu2, XIE Lei2, PAN Ting-ting1
(1.College of Mathematics, Hunan Institute of Science and Technology, Yueyang 414006, China; 2. Linxiang No.5 Middle School, Linxiang 414300, China)
In this paper, eigenvalues and eigenvectors of matrix and the theories of similarity and congruence of symmetric matrix are used, and the matrix method for solving unitary equations of eighth degree is presented.
symmetric matrix; similarity; congruence; algebraic equation of eight degree
O151.1
A
1672-5298(2014)03-0018-05
2014-06-21
国家自然科学基金项目(11371074); 湖南省教育厅科研项目(13C366); 2014年湖南理工学院大学生研究性学习和创新性实验计划项目
万正苏(1976− ), 男, 湖南桃江人, 博士, 湖南理工学院数学学院副教授. 主要研究方向: 微分方程数值解
