直齿面齿轮啮合效率计算研究*
2014-07-05苏进展贺朝霞
□ 苏进展 □ 贺朝霞
长安大学 道路施工技术与装备教育部重点实验室 西安 710064
面齿轮传动是圆柱齿轮与平面齿轮啮合的角度传动,可用于两齿轮轴线正交、非正交或偏置等情况[1]。面齿轮副应用在分流-汇流传动中,发挥了独特的优越性,在航空传动领域的应用表现出了潜在的优势。但是国内对于其啮合效率的研究很少,而对圆柱齿轮啮合效率做了大量的研究[2-4],但摩擦因数大多采用平均值或由半经验公式算得,赵宁等采用CFD(Computational FluidDynamics)计算面齿轮风阻功率损失[5]。 本文在直齿面齿轮几何接触分析[6]和齿轮承载接触分析[7]的基础上,利用热弹流理论得到接触线上各点处的滑动摩擦因数,进而得到了直齿面齿轮传动的滑动摩擦功率损失。
1 啮合效率的计算流程
直齿面齿轮传动功率损失主要有滑动摩擦功率损失、滚动摩擦功率损失、风阻损失等,其中滑动摩擦功率损失所占比例很大,本文仅考虑滑动摩擦功率损失对啮合效率的影响。
直齿面齿轮传动啮合效率的计算流程如图1所示,主要由齿轮啮合仿真、瞬时摩擦因数计算、啮合效率的计算等组成。以△φ为步长将一个啮合周期分为m 个啮合位置, 对应小轮的转角分别为 φi,i=1,2,3,…,m。在啮合位置φi,由齿轮副的轮齿接触分析(TCA)和轮齿承载接触分析(LTCA)可以得到该位置下各啮合线上各离散点处的法向载荷和载荷密度等;由各离散点的当量曲率半径、相对滑动速度、法向载荷和载荷密度等以及润滑油的动力黏度、齿轮的材料参数等可以得到弹流润滑状态下各离散点的滑动摩擦因数;由求得的法向载荷、相对滑动速度和滑动摩擦因数可以求得位置φi的直齿面齿轮瞬时滑动摩擦功率损失,进而求得瞬时啮合效率。遍历一个啮合周期内各啮合位置的瞬时啮合效率,进而求出直齿面齿轮传动平均啮合效率。
2 滑动摩擦功率损失的计算
直齿面齿轮在承载情况下,由点接触变为近似椭圆的局部接触区,又由于椭圆短轴对于长轴来说非常小,两齿面在该点的接触可以认为是局部线接触,所以该瞬时接触点处的滑动摩擦功率损失为沿椭圆长轴上各点处的摩擦功率损失之和。将接触线离散为有限线段,如图2所示,以各段中点参数表示该段接触线上各点的参数,由各段离散接触线的滑动摩擦功率损失之和近似表示该瞬时接触线的滑动摩擦功率损失。
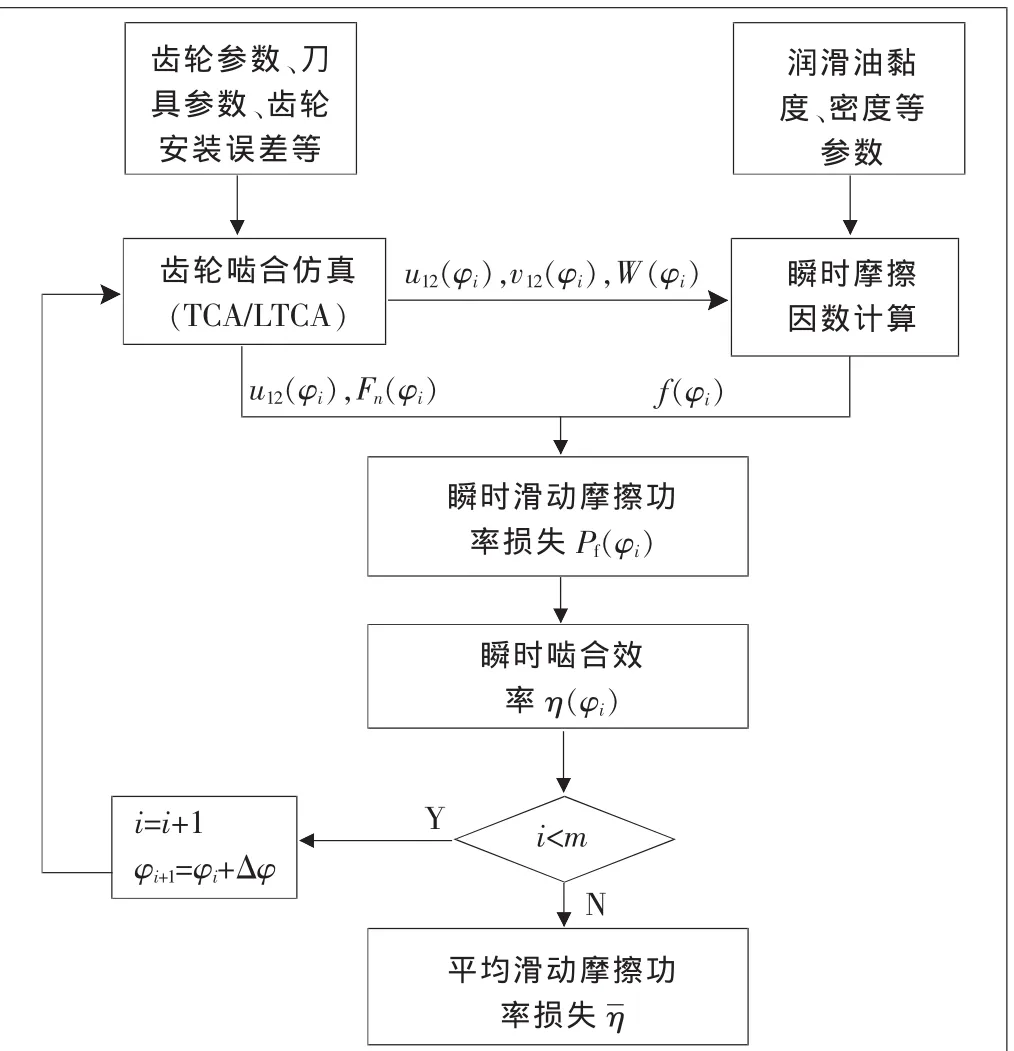
▲图1 啮合效率计算流程
2.1 离散点处的相对滑动速度
忽略齿面间隙和弹性变形量的影响,则两齿面在离散点 Mj处的切向速度和相对滑动速度分别为:式中:分别为小轮和大轮在固定坐标系Sf下,离散点 Mj的速度;分别为向 n(Mj)f方向的投影。

2.2 滑动摩擦因数的计算
齿轮在每段离散的啮合线的润滑情况用两个单位长度当量圆柱的接触情况来模拟,如图3所示,即两个圆柱体沿其母线的接触。图中Wj为两圆柱的法向载荷密度,为当量圆柱的半径,为两当量圆柱表面相对于接触点Mj的运动速度。
如图 4所示,eξ、eη分别为接触椭圆在切平面∑t上的长轴方向和短轴方向,则接触线方向为eξ方向;es、eq为小轮齿面∑1在接触线上任意离散点Mj处的两个主方向;轴eξ与轴eq的夹角为σ[8-9]。等效圆柱的曲率为小轮齿面在离散点Mj处eη方向上的法曲率,由Euler方程可得:

式中:K1eηj为小轮齿面在离散点Mj处eη方向上的法曲率;为小轮齿面在离散点Mj处的两个主曲率。
油膜压力分布和膜厚分布可以通过联立求解Reynolds方程、黏度方程、密度方程、能量平衡方程和载荷方程等求得,根据求得的油膜压力分布、膜厚分布和Ree-Eyring流体的本构方程可以得到油膜中剪应力分布,根据求得的剪应力分布可以求得两接触表面之间的摩擦力和摩擦因数。为了得到较好的收敛性能和较快的计算速度,本文仅仅考虑了热效应和非Newton流动的影响,即建立稳态热弹流理论模型求解滑动摩擦因数。图5所示为接触表面的摩擦力与润滑油的速度分布,图中,x1和x2是油膜的起点和终点位置;F1和F2分别为两表面上所受的摩擦力。滚动摩擦力主要产生于入口区(x1,-b),滑动摩擦力主要产生在接触区(-b,b)内,所以两表面的滑动摩擦力为:

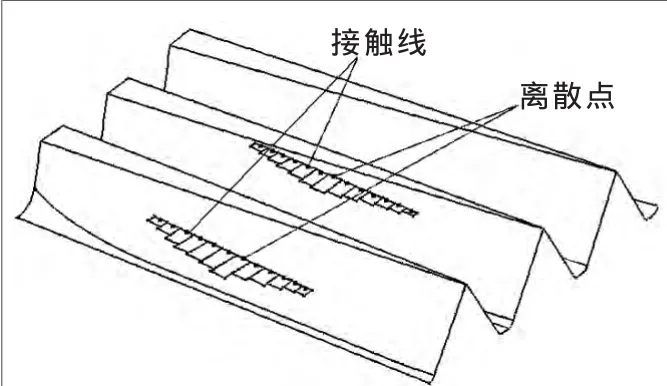
▲图2 接触线离散

▲图3 当量圆柱接触

▲图4 切平面坐标
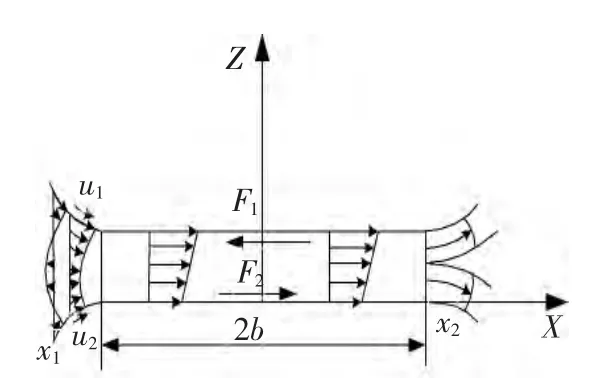
▲图5 速度分布与摩擦力
式中:τ为油膜内剪应力。
滑动摩擦因数为:

将以上数学模型无量纲化,采用多重网格法求解压力,采用逐列扫描技术求解温度,通过压力与温度的反复迭代求得完全数值解,具体方法参见文献[9]。在离散点Mj处,令:通过解以上各式,可得到离散点Mj处瞬时滑动摩擦因数,采用同样的办法,可以依次求得各啮合位置各离散点处的瞬时滑动摩擦因数。

3 啮合效率的计算
啮合位置φi处离散点Mj处的瞬时滑动摩擦因数μj(φi)确定后,该离散点处的滑动摩擦力为:

式中:Fnj(φi)为啮合位置 φi处离散点 Mj处法向载荷。
由一般动力学功率计算方法得到啮合位置φi处齿面滑动摩擦功率损失为:

式中:u(Mj)12(φi)为啮合位置 φi处离散点 Mj处两齿面相对滑动速度;n(i)为啮合位置φi处离散点的个数。
仅考虑滑动摩擦功率损失情况下,直齿面齿轮在啮合位置φi处瞬时啮合效率为:

式中:Pin为齿轮的输入功率。
由上述计算可以得到一个啮合周期内各啮合位置φ1、φ2、..、φm对应的瞬时啮合效率 η(φ1)、η(φ2)、..、η(φm),由最小二乘法拟合得到小轮转角与瞬时啮合效率的关系式:

沿啮合周期内对小轮转角积分求平均值,得到直齿面齿轮的平均啮合效率:

4 算例分析
以一对直齿面齿轮为例计算其啮合效率,齿轮的参数如表1所示。图6分别为啮合线上离散点的法向载荷、相对滑动速度和滑动摩擦因子,高度为h的离散点的值表示为hc/h0,h为离散点的高度(如图所示),h0为标度的高度,c 为标度(即 c=1m/s、500N、0.1)。 图 7为齿轮啮合效率随小轮转角的变化曲线,其中小轮转过的角度为一个周期。齿轮的输入功率为73.3kW, 输入转速为1000r/min。
由图6可以看出节线附近的相对滑动速度很小,离节线越远的啮合线上点的相对滑动速度越大;不同啮合线上离散点的滑动摩擦因数不同,同一啮合线上不同离散点的滑动摩擦因数也不同。由图7可以看出,齿轮在不同位置的啮合效率不同,积分得到齿轮的平均啮合效率为 0.98808。

表1 齿轮参数
图8所示为一单位长度圆柱与平面接触时不同滑滚比、不同载荷密度下的滑动摩擦因数,此时吸油速度为3.0m/s。在载荷密度是1000N/mm的条件下,图9所示为不同滑滚比、不同卷吸速度下的滑动摩擦因数。其中,圆柱半径为 0.08m,滑滚比 Sr=2(u1-u2)/(u1+u2)。

▲图6 旋转投影面上相对滑动速度、法向载荷和滑动摩擦因数

▲图7 啮合效率曲线

▲图8 滑动摩擦因数
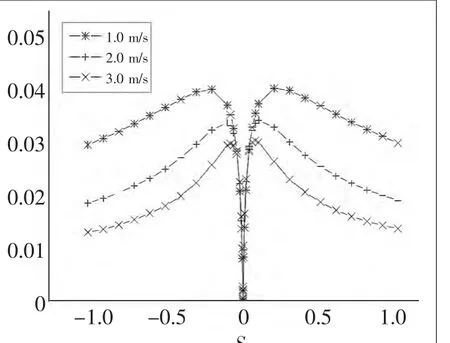
▲图9 滑动摩擦因数(W=1000N/mm)

▲图10 齿轮平均啮合效率
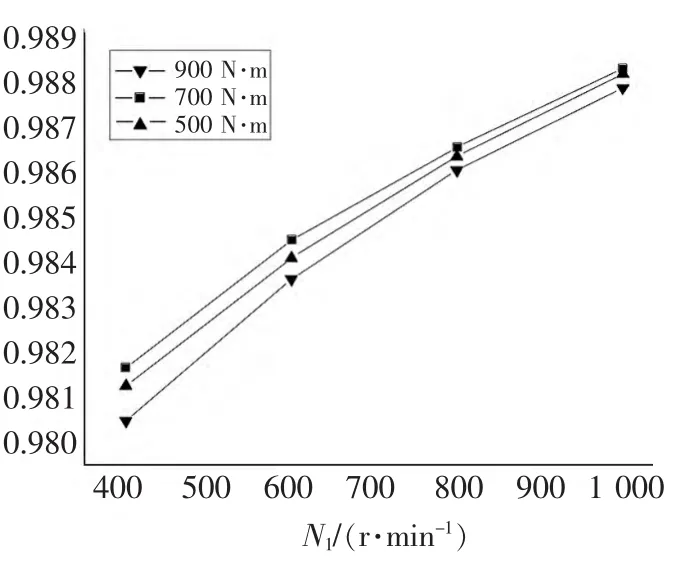
▲图11 齿轮平均啮合效率(本文所述算法)
由图8、9可以看出,滑动摩擦因数随滑滚比的减小先增大后减小,在纯滚动处,滑动摩擦因数为零。相对滑动摩擦因数随齿轮所承受法向载荷密度的增大而增大,随齿轮卷吸速度的增大而减小。
图10所示为假设齿轮摩擦因数为一固定值0.1、不同输入扭矩下直齿面齿轮啮合效率随转速的变化曲线,图11所示为本文所述算法求得的不同输入扭矩下直齿面齿轮啮合效率随转速的变化曲线。
图10中假定齿面摩擦因数为一固定值,则齿轮的啮合效率随转速和扭矩的变化都不大;图11是由本文计算模型得到的啮合效率,随转速增大而增大,随扭矩增大而减小。说明转速和扭矩对啮合效率的影响主要是通过摩擦因数实现的。
5 结论
通过以上分析可以得到以下结论。
(1)热弹流理论及其数值解法的发展使热弹流理论可以用于求解齿轮的传动效率,提高齿轮传动效率的计算精度。
(2)齿面上不同位置的滑动摩擦因数也不相同,且不同工况下齿面上同一位置的滑动摩擦因数也不相同,因此采用平均摩擦因数来计算啮合效率有一定的偏差。
(3)齿面滑动摩擦因数是影响齿轮啮合效率的重要因素,扭矩、转速对啮合效率的影响是通过影响摩擦因数实现的。仅考虑滑动摩擦功率损失情况下,齿轮啮合效率随滑动摩擦因数的减小而增加。
(4)扭矩、转速是影响滑动摩擦因数的重要因素,齿面滑动摩擦因数随扭矩的增大而增大,随转速的增大而减小。
[1] 朱如鹏,高德平.面齿轮传动的研究现状与发展 [J].南京航空航天大学学报,1997,29(3):357-362.
[2] 王成,方宗德,贾海涛.斜齿轮滑动摩擦功率损失的计算[J].燕山大学学报, 2009, 33(2):99-102.
[3] 王成,高常青,贾海涛.基于人字齿轮啮合特性的滑动摩擦功率损失[J].中南大学学报 (自然科学版),2012,43(6):2174.
[4] Seetharaman S.An Investigation of Load-independent Power Losses of Gear Systems [D]. Columbus:Ohio State University, 2009.
[5] 赵宁,贾清健.基于 CFD的面齿轮风阻功率损失研究[J].机械传动, 2012, 36(9):4-7.
[6] 沈云波,方宗德,赵宁,等.考虑边缘接触直齿面齿轮传动轮齿接触分析[J].机械传动, 2009, 33(1):9-13.
[7] 沈云波,方宗德,赵宁,等.考虑边缘接触直齿面齿轮传动承载接触分析 [J].机械科学与技术,2009(8):1096-1100.
[8] Litvin F L, Fuentes A.Gear Geometry and Applied Theory[M].Cambridge University Press, 2004.
[9] 鲁文龙,朱如鹏,曾英.正交面齿轮传动中齿面曲率研究[J].南京航空航天大学学报, 2000, 32(4):400-404.
[10] 杨沛然.流体润滑数值分析[M].北京:国防工业出版社,1998.
