相对论框架下脉冲星导航的2PN观测方程
2014-07-05任红飞魏子卿周庆勇
任红飞,魏子卿,周庆勇
1.地理信息工程国家重点实验室,陕西西安 710054;2.西安测绘研究所,陕西西安 710054
相对论框架下脉冲星导航的2PN观测方程
任红飞1,2,魏子卿1,2,周庆勇1,2
1.地理信息工程国家重点实验室,陕西西安 710054;2.西安测绘研究所,陕西西安 710054
介绍了脉冲星导航的研究进展,顾及天体的四极矩和角动量,推导了脉冲星导航的2PN观测方程,对导航观测方程中的2PN相对论效应进行数值分析。结果表明:在脉冲星导航中,太阳系天体的四极矩和角动量导致的时间延迟在10-13s量级;太阳对信号传播的引力弯曲不足1 ns,太阳系行星对信号的引力弯曲以木星为最大,量级为10-18s。
脉冲星导航;观测方程;相对论效应
1 引 言
关于脉冲星导航的构想最早产生于1974年[1]。天文观测卫星发射以后,文献[2]提出了用X射线脉冲星为近地卫星乃至星际飞行器导航的构想;文献[3]用HEAO-A1卫星实测数据对X射线脉冲星定姿方法进行验证;斯坦福大学线性加速器中心和美国海军实验室开展了USA试验,主要目的是验证脉冲星导航的可行性[4]。目前,世界主要大国都开展了相关的研究计划。美国DARPA于2005年提出了XNAV计划[5],最终目的是实现10 m(3σ)的定位精度;2004年,欧空局完成了脉冲星导航可行性研究[6];2009年,俄罗斯披露了其在该领域的一些研究进展,2012年3月30日,德国马克斯-普朗克研究院报道了其在脉冲星导航方面的研究进展。
导航观测方程是研究脉冲星导航的理论基础。文献[7—8]推导了1PN度规形式下的脉冲星计时观测方程;文献[14]推导脉冲星天文定时观测中的高阶相对论效应;文献[10]给出了1PN度规形式下的脉冲星导航观测方程;文献[15]研究了X射线脉冲星导航的测量方程和相对论修正公式。随着脉冲星观测精度的提高,观测方程的精度也要相应提高。在1PN度规形式下,脉冲星导航观测方程的理论精度约为10-9s[14,16],为满足更高精度的观测需求,就要考虑观测方程的高阶相对论效应。在2PN导航观测方程的研究方面,文献[15]中仅考虑了太阳和地球的自转,没有考虑四极矩,文献[11,17]没有考虑时空交叉项的影响。
2 2PN导航观测方程的推导
由于时空特性由度规确定,因此脉冲星导航观测方程的推导需以确定的度规形式为前提。观测方程推导的基本思路为:首先确定太阳系各个天体的度规2PN形式,然后将局部参考系下度规势转换到整体参考系下,再利用测地线方程推导光子的光行时,进而得到2PN导航观测方程。
2.1 度规势及其转换
在广义相对论理论中,考虑太阳的自转与四极矩,并假定太阳的自转轴与对称轴重合,太阳的2 PN度规为[9,14]
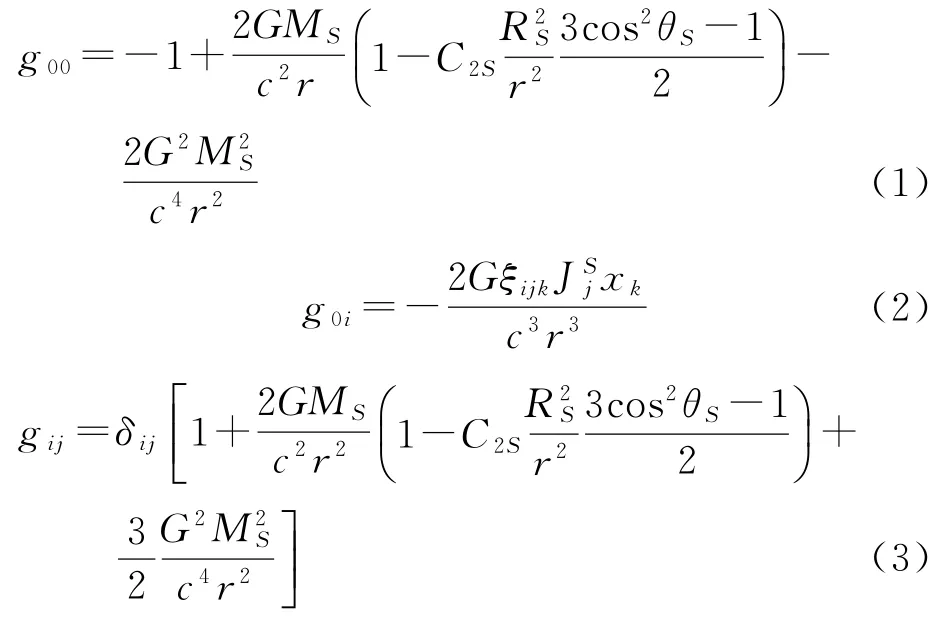
式中,r为场点到太阳质心的距离;c为真空光速;G为引力常数;MS为太阳质量;C2S为太阳无量纲四极矩;RS为太阳半径;JSj为太阳的角动量在j方向的分量;θS为场点位矢与太阳对称轴之间的夹角;ξijk为Levi-Civita记号。
由于太阳系各行星与太阳较为相似,同样可以写出顾及行星自转和四极矩的2PN度规。但这个度规局限于各个天体局部坐标系,在讨论整个太阳系的度规形式时,需要将各个天体的局部度规和时空坐标转换到整体坐标系下。DSX体系下,局部度规势与整体度规势之间的转换关系为[18]
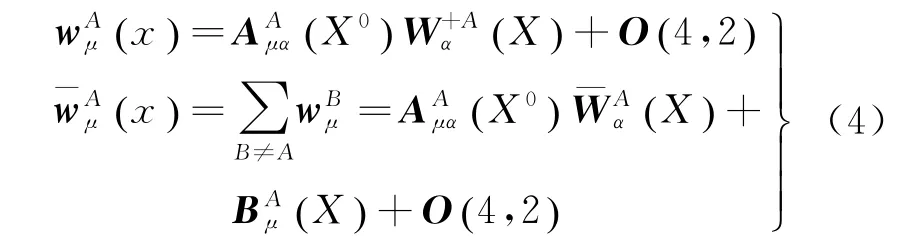
2.2 脉冲信号的TOA方程
由于太阳系各行星与太阳较为相似,因此在局部坐标系下,太阳系行星的度规形式与式(1)—式(3)相似,在讨论整个太阳系的度规形式时,需要将各个天体的局部度规和时空坐标转换到整体坐标系下。由于度规势转换对脉冲TOA的影响微小,在此可将整个太阳系的2 PN度规可写为
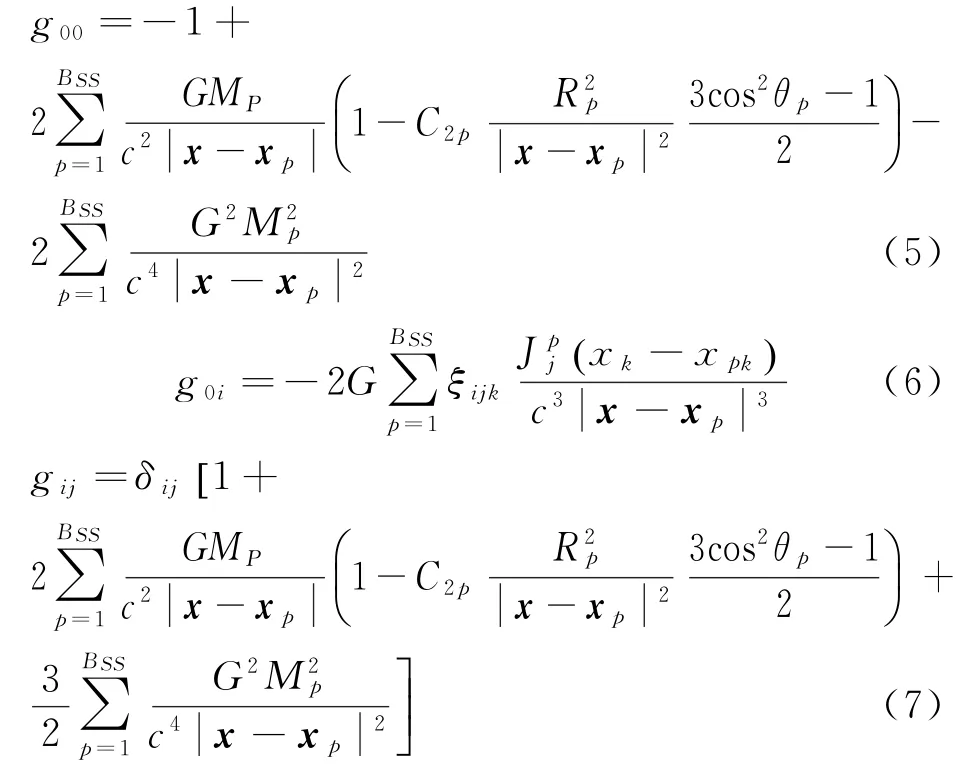
式中,BSS为太阳系天体总数;Mp为太阳系中第p个天体的质量;x为场点相对于太阳质心的位矢;xP为第p个天体的质心相对于太阳质心的位矢;C2p为第p个天体的四极矩常数;Jpj为第p个天体的角动量在j方向的分量。
X射线脉冲星的轮廓由若干光子的TOA按照一定的时间间隔折叠得到,每个光子在空间沿自己的世界线传播。根据相对论理论,电磁信号在时空中传播的世界线为零测地线,满足以下表达式[19]
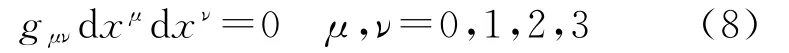
脉冲星距离地球十分遥远,其信号传播路径上所有物质(包括天体和介质等)的位置、速度、质量等参数很难精确确定,因此理论上很难精确确定脉冲星信号从脉冲星到地球的传播路径。但太阳系以外的天体对信号传播的相对论效应在几十年的时间段内可视为常数[7-8],因此仅需考虑太阳系内天体对信号传播的相对论效应。另外,太阳系天体时刻都处于运动状态,而脉冲星信号在太阳系内以光速传播,掠过太阳系需要一定时间,而在讨论相对论问题时,需要用到某一时刻的太阳系天体位置,考虑到太阳系天体的公转周期相对较长,信号传播时间很短,在短时间段内太阳系天体的位置变化很小,不会影响相对论效应的估计,因此可假定太阳系天体位置的时标为信号到达观测者的时刻。
为推导信号传播的TOA方程,现建立如图1所示的坐标系,以太阳质心、脉冲星和飞行器3点所确定的平面为xy平面,并且取x轴平行于信号传播方向,y、z坐标轴按右手定则确定。其中d为太阳质心至信号传播路径的距离,di为太阳系内天体Mi至信号传播路径的距离,一般不在xy平面内。
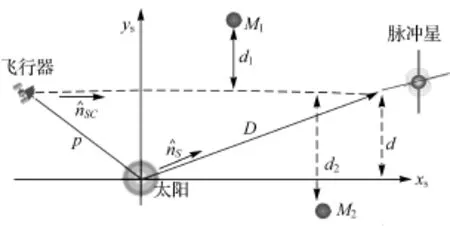
图1 信号由脉冲星到达飞行器的示意图Fig.1 The path of signals from pulsar to the spacecraft

由x轴平行于信号传播方向可得如下表达式近似取v=c(,0,0),将式(9)中代入式(8),可得考虑到式(5)—式(7),式(10)可进一步写为
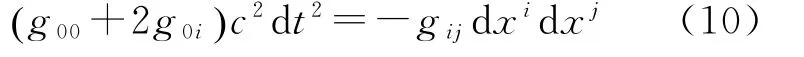

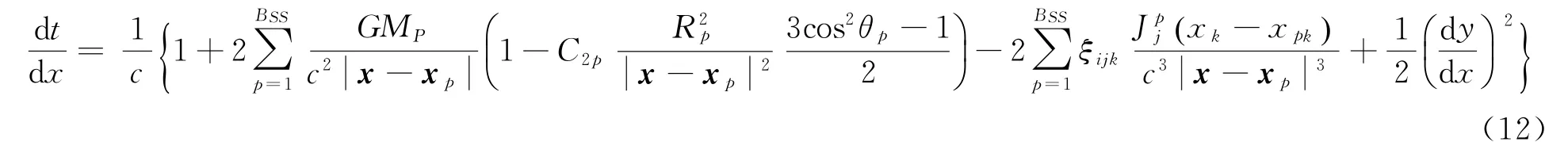
式(11)准确到O 4()后,可改写为又有信号传播路径满足类光测地线方程[7]
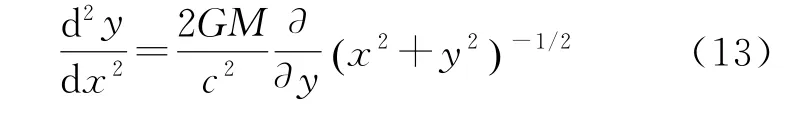
式中,GM为天体的度规势。根据初始条件d y/ d x=0、x=Dx、y=d,可解得信号传播的空间轨迹的一阶摄动解为
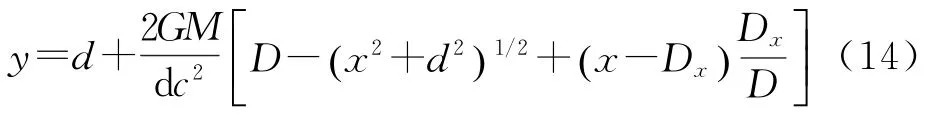
式中,D为矢量D的模,对式(12)两边关于x求导数,得到
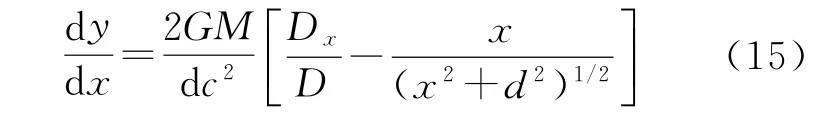
将式(15)代入式(12)中,可得
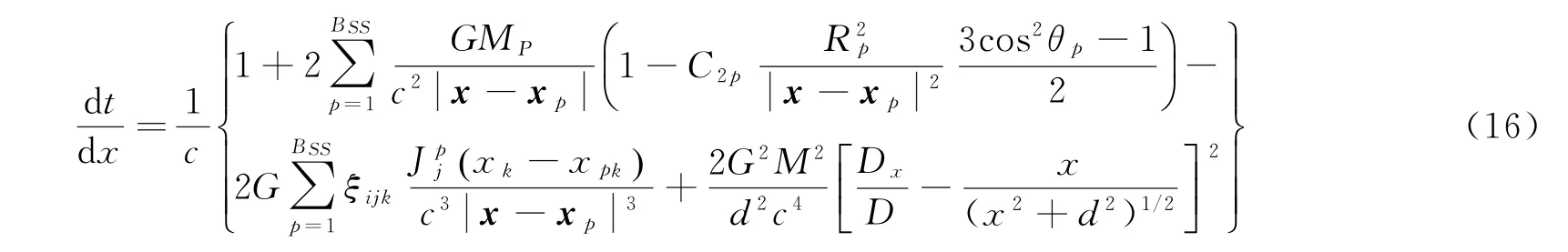
由于xy平面与太阳的自转轨道面一般不重合,因此有
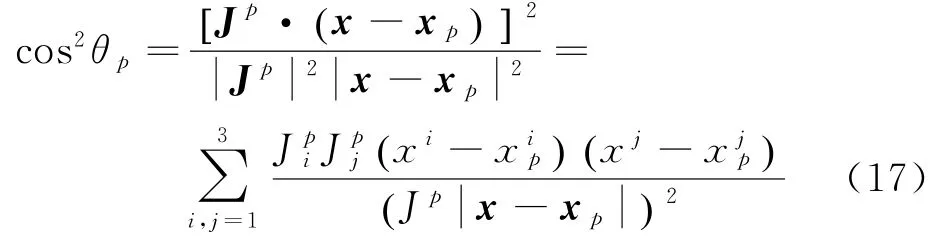
因为信号传播路径近似平行于x轴,其差异对到达时间的影响为O 5(),在此可忽略,因此有y= d、z=0,故式(17)可进一步改写为
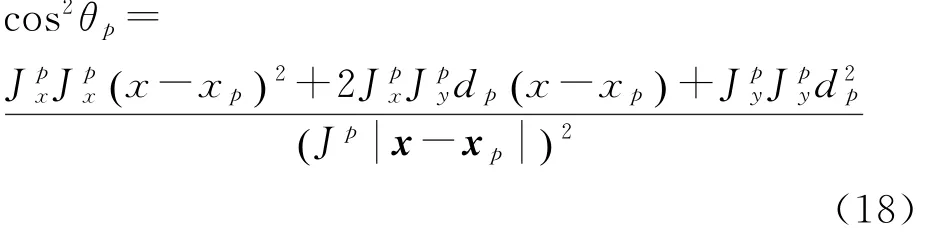
式中的dp为常数,代表第p个天体到信号传播路径的距离。将式(18)代入式(16)后可得

T为信号发射时刻,t为接收时刻。式(19)的积分结果为

式中
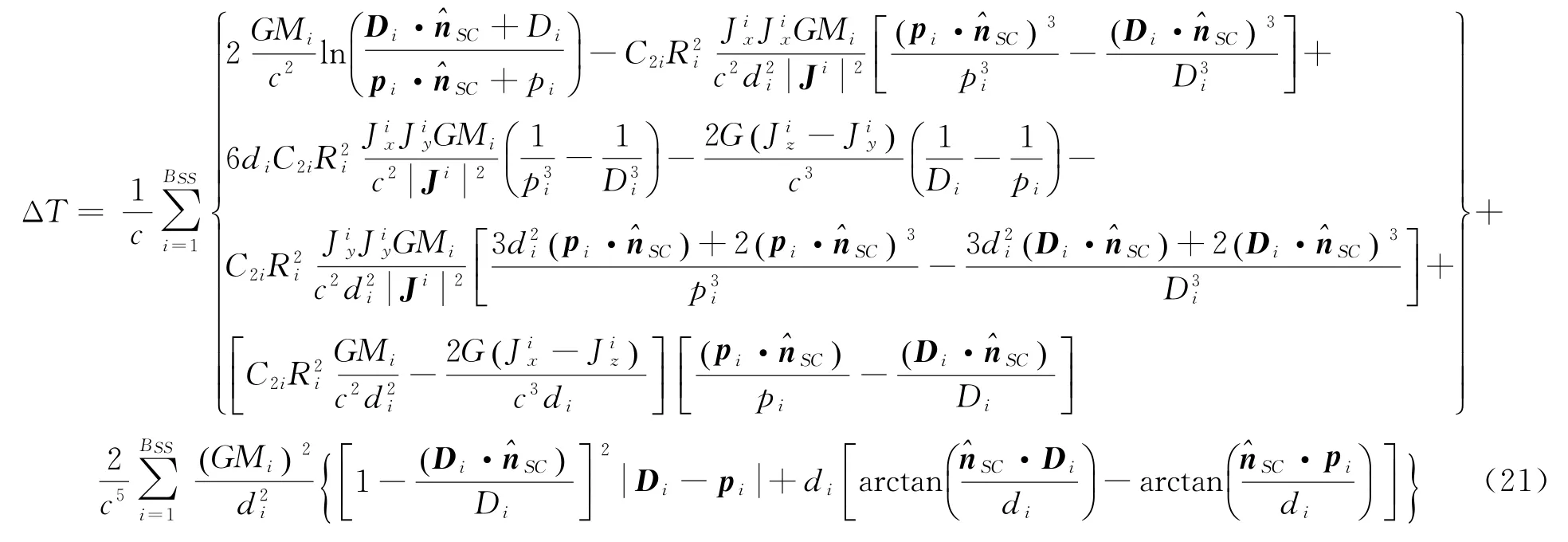

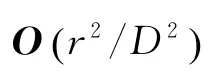
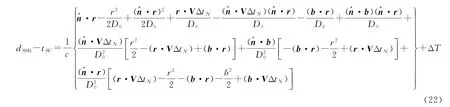

仿真分析导航观测方程中的2PN相对论效应。
3 2PN相对论效应的数值分析
3.1 数值条件
为分析脉冲星导航中的相对论效应,给定以下计算条件:①模拟绕地飞行器的轨道根数见表1;②3颗脉冲星的参数信息见表2;③太阳系内各个天体的位置由JPL DE405历表给出。
在二体力学模型下,根据表1中6个轨道根数可以仿真计算出飞行器在任一时刻的位置和速度。表2中3颗脉冲星的参数可参见文献[12—13],由地面射电观测获得。

表1 飞行器轨道根数Tab.1 Orbit elements of the spacecraft

表2 X射线脉冲星的参数值Tab.2 Parameters of X-ray pulsars
注:距离单位kpc为千秒差距(1 kpc=3260光年=3.08×1019m);MJD表示约化儒略日。
需要指出的是,这里之所以采用数值仿真是由于相对论问题通常要在较大尺度的时空范围内考虑,且2PN相对论效应量级较小,飞行器的位置误差不会影响相对论效应的评估,同时采用数值仿真更有利于分析2PN相对论效应的长期变化情况。
3.2 计算结果
3.2.1 太阳系天体的四极矩和角动量导致的时间延迟
图2为自2012年1月1日起,观测脉冲星B0531+21 2000 d,太阳、地球、月球以及木星的四极矩和角动量导致的时间延迟。由图可见,太阳和地球的自转和四极矩和角动量导致的时间延迟在量级上相当,且呈现周期性变化。

图2 不同太阳系天体的四极矩和角动量所导致的时间延迟Fig.2 Time delay due to angular momentum and quadruple moment of different celestial bodies in solar system
图3为观测不同脉冲星时,太阳系内天体的自转和四极矩所导致的时间延迟。由图可见,观测不同脉冲星,太阳系天体的四极矩和角动量所导致的时间延迟在量级上相当。
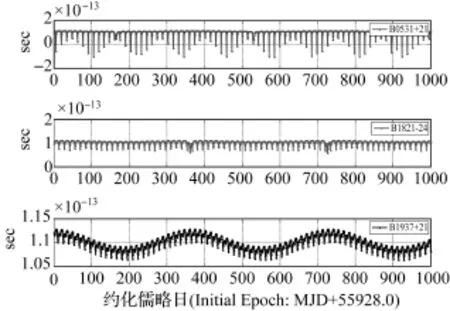
图3 观测不同脉冲星时太阳系天体的四极矩和角动量所导致的时间延迟Fig.3 Time delay due to angular momentum and quadruple moment of celestial bodies in solar system for different pulsars
综合以上两图可知在基于脉冲星观测的近地飞行器自主导航中,太阳系天体的四极矩和角动量所导致的时间延迟在10-13s量级,不同脉冲星的时间延迟量级基本一致,且存在周期性变化。
3.2.2 太阳系天体引力弯曲导致的时间延迟
图4为自2010年1月1日起,观测3颗脉冲星1000 d,太阳引力弯曲导致的时间延迟。
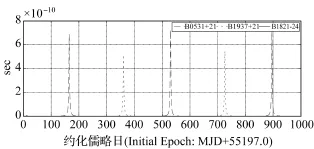
图4 太阳引力弯曲Fig.4 Time delay of the path bending due to the Sun
由图4可见,在1000 d的仿真时间内,太阳引力弯曲导致的时间延迟不足1 ns。
图5为自2010年1月1日始,观测脉冲星B0531+21 10 000 d,太阳系行星引力弯曲导致的时间延迟。
由图可见对于近地飞行器,木星的引力弯曲最大,量级为10-18s。由于影响微小,因此所有行星的引力时延可忽略。
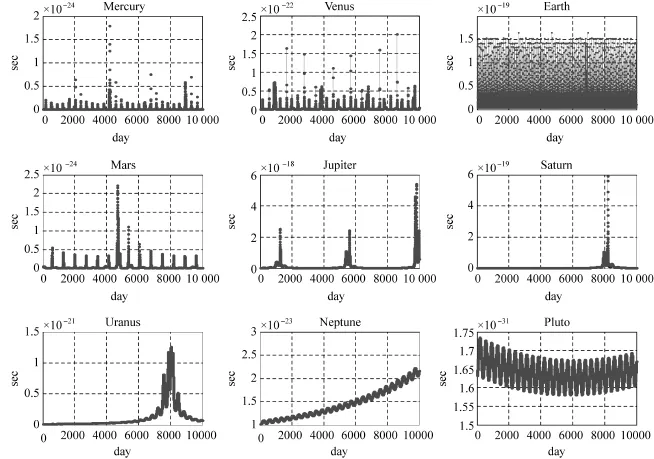
图5 行星引力弯曲Fig.5 Time delay of the path bending due to planets in solar system
4 结 论
观测方程是脉冲星导航理论研究的重要部分。论文介绍了脉冲星导航的研究进展,顾及天体的四极矩和角动量,推导相对论框架下脉冲星导航的2PN观测方程,对导航观测方程中的2PN相对论效应进行数值分析。结果表明:在脉冲星导航中,太阳系行星对信号的引力弯曲以木星为最大,量级仅10-18s;太阳对信号传播的引力弯曲在1 ns以内,太阳系行星的四极矩和角动量导致的时间延迟在10-13s量级。综合以上因素,脉冲星导航中,2PN相对论效应的影响不足1 ns。
目前,已有观测方程中考虑了部分高阶相对论效应,如Tempo2脉冲星计时软件中就考虑了太阳引力时延影响[20]。由于空间观测水平的限制,当前脉冲星导航观测方程中还未考虑2PN相对论效应,但随着观测水平的提高,2PN相对论效应将会成为高精度观测方程的组成部分。此外,从理论研究角度看,脉冲星导航中的2PN相对论效应也是从实践上验证广义相对论理论的又一途径。
[1] DOWNS G S.Interplanetary Navigation Using Pulsation Radio Sources[R].[S.l.]:NASA,1974.
[2] CHEST T J,BUTMAN S A.Navigation Using X-ray Pulsars [R].[S.l.]:NASA,1981.
[3] HANSON J E.Principles of X-ray Navigation[D].Palo Alto:Stanford University,1996.
[4] WOOD K S,DETERMAN J R.Using the Unconventional Stellar Aspect(USA)Experiment on ARGOS to Determine Atmospheric Parameters by X-ray Occultation[C]∥Proceedings of International Society of Optical Engineering (SPIE).Nashville:[s.n.],2002:258-265.
[5] GRAVEN P,COLLINS J,SHEIKH S,et al.XNAV Beyond the Moon[C]∥Proceedings of ION 63rd Annual Meeting.Cambridge:[s.n.],2007:423-431.
[6] SALE J,URRUELA A,VILLARES X,et al.Feasibility Study for a Spacecraft Navigation System Relying on Pulsar Timing Information[R].[S.l.]:ESA,2004.
[7] HELLING R W.Relativistic Effects in Astronomical Timing Measurement[J].The Astronomical Journal,1986, 91(3):650-659.
[8] BACKER D C,HELLING R W.Pulsar Timing and General Relativity[J].Annual Review of Astronomy and Astrophysics,1986,24:537-575.
[9] RICHTER G W,MATZNER R A.Second-order Contribution to Relativistic Time Delay in the Parameterized Post-Newtonian Formalism[J].Physical Review D,1983, 26(10):3007-3012.
[10] SHEIHK SI.The Use of Variable Celestial X-ray Sources for Spacecraft Navigation[D].Baltimore:University of Maryland,2005.
[11] SHEIHK S I,HELLINGS R W,MATZNER R A.Highorder Pulsar Timing for Navigation[C]∥Proceedings of ION 63th Annual Meeting.Cambridge:[s.n.],2007:432-443.
[12] GRAVEN P,COLLINS J,SHEIHK SI,et al.XNAV for Deep Space Navigation[C]∥Proceedings of 31st Annual AAS Guidance and Control Conference.San Diego:[s.n.], 2008:1-16.
[13] SHEIKH S I,PINES D J,RAY P S,et al.Spacecraft Navigation Using X-ray Pulsars[J].Journal of Guidance, Control,and Dynamics,2006,29(1):49-63.
[14] LIU Jiaqiu,XU Chongming.The High Order Relativistic Effects in Millisecond Pulsar Timing[J].Acta Astronomica Sinica,1989,30(3):323-332.(刘甲求,须重明.毫秒脉冲星天文定时观测中的高阶相对论效应[J].天文学报, 1989,30(3):323-332.)
[15] FEI Baojun.Application of Relativity in Modern Navigation [M].Beijing:National Defense Industry Press,2007.(费保俊.相对论在现代导航中的应用[M].北京:国防工业出版社,2007.)
[16] REN Hongfei,WEI Ziqing ZHAI Zhenhe,et al.The Timing Equation of Pulsar Navigation in 1PN Approximation and Its Accuracy Analysis[J].Acta Geodaetica et Cartographica Sinica,2012,41(1):41-47.(任红飞,魏子卿,翟振和,等.1PN近似下脉冲星导航的观测方程及精度分析[J].测绘学报,2012,41(1):41-47.)
[17] SHUAI Ping,LI Ming,CHEN Shaolong,et al.Principles and Methods for X-ray Pulsar Navigation System[M].Beijing:China Astronautic Publishing Press,2009.(帅平,李明,陈绍龙,等.X射线脉冲星导航系统原理与方法[M].北京:中国宇航出版社,2009.)
[18] XU Chongming,WU Xuejun.General Relativity and Modern Cosmology[M].Nanjing:Nanjing Normal University Press,1999.(须重明,吴雪君.广义相对论与现代宇宙学[M].南京:南京师范大学出版社,1999.)
[19] REN Hongfei.The Research on Timing Model of the Pulsar Navigation in the General Theory of Relativity[D].Zhengzhou:Information Engineering University,2012.(任红飞.相对论框架下脉冲星导航模型的研究[D].郑州:信息工程大学,2012.)
[20] HOBBS G B,EDWARDS R T,MANCHESTER R N.TEMPO2,a New Pulsar Timing Package.I:Overview [J].Monthly Notices of Royal Astronomical Society, 2006,369(2):655-672.
(责任编辑:宋启凡)
The 2PN Observation Equation for Pulsar Navigation in Framework of General Relativity
REN Hongfei1,2,WEI Ziqing1,2,ZHOU Qingyong1,2
1.National Key Laboratory of Geo-Information Engineering,Xi’an 710054,China;2.Xi’an Research Institute of Surveying and Mapping,Xi’an 710054,China
Advance of theory and applications in the pulsar navigation are first briefly reviewed,then considering the angular momentum and quadruple moment of celestial bodies in solar system,the 2PN observation equation for pulsar navigation is derived,and the numerical simulations for 2PN relativistic effects are analyzed.Results show that the relativistic effects of angular momentum and quadruple moment of celestial bodies in solar system are about 10-13s,the light ray bending due to the sun is less than 1 ns, the light ray bending due to the Jupiter is 10-18s,which is the largest among the solar system planets.
pulsar navigation;observation equation;relativistic effects
REN Hongfei(1984—),male,PhD,majors in space geodesy and navigation.
P228
A
1001-1595(2014)10-1025-07
2013-07-20
任红飞(1984—),男,博士,研究方向为空间大地测量与导航。
E-mail:renhongfei336@163.com
REN Hongfei,WEI Ziqing,ZHOU Qingyong.The 2PN Observation Equation for Pulsar Navigation in Framework of General Relativity[J].Acta Geodaetica et Cartographica Sinica,2014,43(10):1025-1031.(任红飞,魏子卿,周庆勇.相对论框架下脉冲星导航的2PN观测方程[J].测绘学报,2014,43(10):1025-1031.)
10.13485/j.cnki.11-2089.2014.0142
修回日期:2013-12-20
