采用Xu-White模型进行横波预测影响因素分析

孙 璞，高 刚，胡瑞卿，林耀庭

（1.长江大学油气资源与勘探技术教育部重点实验室,湖北 武汉 430100；2.长江大学地球物理与石油资源学院，湖北 武汉 430100）

纵横波速度是连接岩石各种物理性质与地震波勘探的桥梁，在储层的岩性、物性和流体识别等方面有着重要的应用，然而在实际生产中由于各种原因导致横波信息的缺乏[1-2]。为了获得准确的横波速度，国内外诸多地球物理工作者提出了经验公式和理论模型公式，Castagna，Han等人给出了不同岩性的纵横波速度经验公式[3-5]；Xu等在综合考虑了泥质砂岩中基质性质、泥质含量、孔隙度大小、孔隙形状和孔隙流体之后提出了Xu-White模型计算横波速度[6-7]；李维新等提出基于约束条件横波速度反演和流体替代，改善了预测的精度[8]；熊晓军等提出了基于等效弹性模量反演的横波预测方法，有效地提高了横波速度估算的精度和可靠性[9]。

采用Xu-White模型预测横波，在数值模型试验的基础上分析孔隙纵横比、含水饱和度、泥质含量对Xu-White模型预测横波的影响大小，通过一口有横波测井的资料进行验证，结果表明：综合考虑误差影响因子的改进Xu-White模型预测结果与实际情况吻合良好。

1 基本原理

1.1 横波速度计算原理

地震波在均匀、各向同性、弹性介质中的传播速度表示如下[10]：

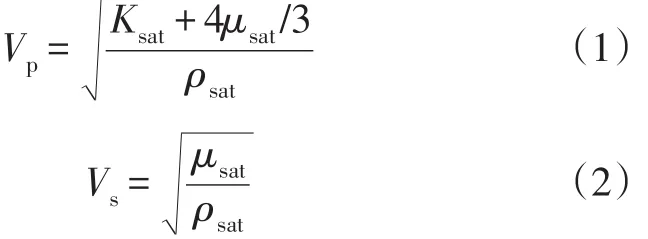
式中：Vp为纵波速度，km/s；Vs为横波速度，km/s；ρsat为饱和岩石的密度，g/cm3；Ksat(Gpa)和μsat(Gpa)分别为饱和岩石的体积模量和剪切模量。

基于Gassmann方程的饱和岩石体积模量和剪切模量表达形式如下：

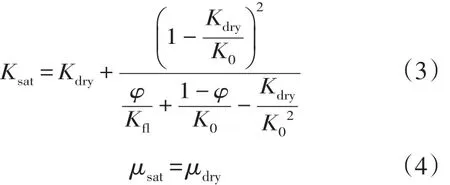
式中：K0为组成岩石矿物的体积模量；Kdry为干岩石骨架体积模量；Kfl为孔隙流体的体积模量；φ为孔隙度；μdry为干岩石的剪切模量。一般采用V-R-H模型求取K0，用Wood公式求取Kfl，该文采用Xu-White模型求取Kdry和μdry。

1.2 Xu-White模型

Xu-White模型针对饱含流体的泥质砂岩，把泥质砂岩的孔隙划分为具有较小孔隙纵横比的泥岩孔隙和具有较大孔隙纵横比的砂岩孔隙，利用Kuster-Toksöz模型和微分等效介质理论（DEM）计算了饱含孔隙流体岩石的体积模量和剪切模量。具体的表达形式如下：

式中：φ为总孔隙度；φc和φs为泥岩和砂岩的孔隙度；vc和vs为其对应的体积百分含量；Kdry，K0和Kfl分别为干岩石、组成岩石矿物和孔隙流体的体积模量；μdry，μ0和μfl分别为其对应的剪切模量。F(α) ，Tijij(α)和Tiijj(α)为与孔隙纵横比α相关的函数。对于干岩石而言，Kfl和μfl均等于零。

为了提高计算效率，Keys和Xu将对K-T方程求解转化为对线性常微分方程组求解，用以求取岩石骨架弹性模量，近似表达式为：

式中：K(φ)和μ(φ)分别表示孔隙度为φ岩石的体积模量和剪切模量。通过统计分析，典型的泥岩孔隙扁率为0.035，砂岩为0.12。

2 横波速度预测的误差分析

为了深入的了解泥质含量、含水饱和度和砂岩孔隙纵横比对基于Xu-White模型横波预测的误差影响情况建立了以下三个模型，并对其进行具体的研究和分析。

2.1 泥质含量对纵横波速度的影响

针对泥质含量对纵横波速度的影响设计了一个饱含气水的砂泥岩模型1，含水饱和度20%，含气饱和度80%，泥质含量的变化范围为0%～80%，其他的详细参数见表1。

表1 模型1的岩石物理参数Table 1 Petrophysical parameters of model 1

试验中孔隙度的变化范围为1%～20%，取样间隔为1%，利用Xu-White模型计算不同泥质含量情况下的纵横波速度，得到的纵波、横波速度随泥质含量的变化情况（图1、图2）。

从图1和图2中可以看出：随着泥质含量的增加，纵横波速度逐渐减小，在孔隙度1%～20%的范围内，泥质含量对纵横波速度的影响一直很大，这说明岩石的矿物组成成分对横波预测会产生很大的误差，所以在利用Xu-White模型进行横波预测时，应尽量保证泥质含量准确性。

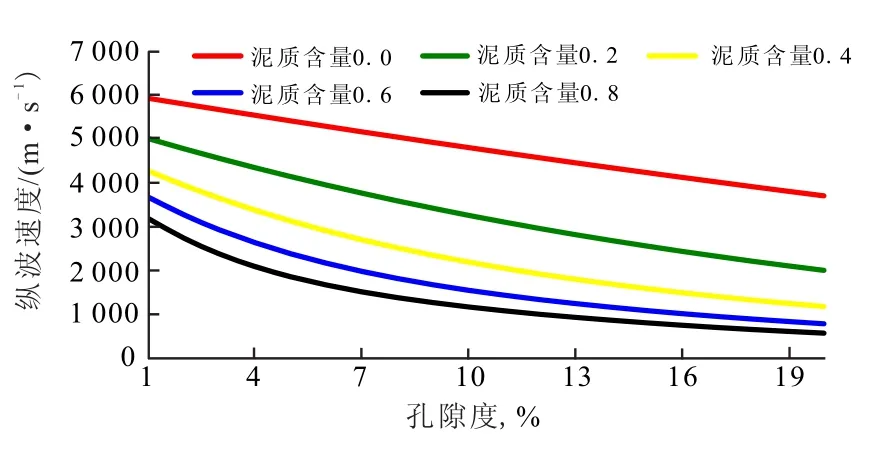
图1 泥质含量对纵波速度的影响Fig.1 The effects of shale content on longitudinal velocity

2.2 含水饱和度对纵横波速度的影响

针对含水饱和度对纵横波速度的影响设计了一个饱含气水的砂泥岩模型2，泥质含量为20%，含水饱和度为0%～100%，其他的参数与表1相同。

试验中孔隙度的变化范围为1%～20%，取样间隔为1%，利用Xu-White模型计算不同含水饱和度情况下的纵横波速度，得到的纵波、横波速度随含水饱和度的变化情况（图3、图4）。

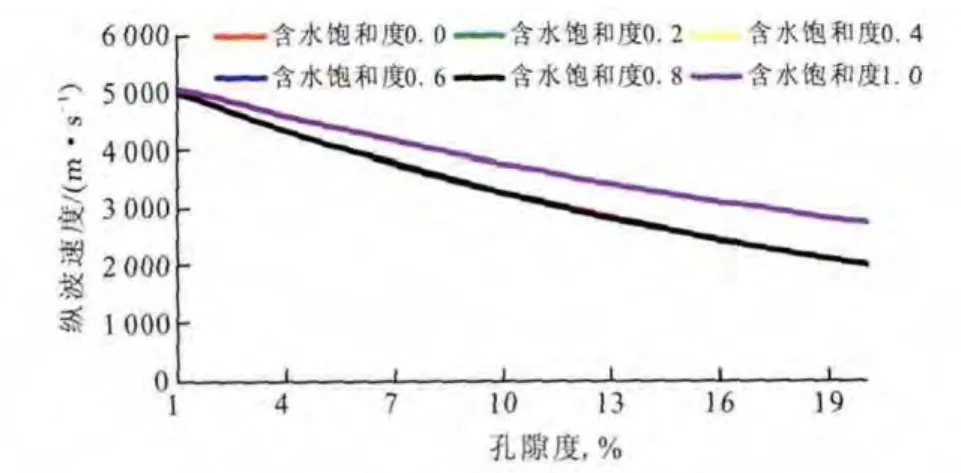
图3 含水饱和度对纵波速度的影响Fig.3 The effects of SW on longitudinal velocity

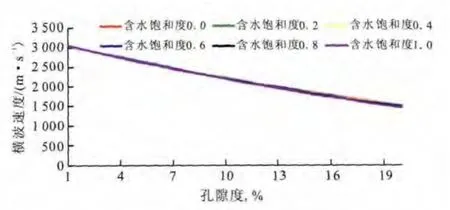
图4 含水饱和度对横波速度的影响Fig.4 The effects of SW on shear velocity

从图3和图4可以看出：随着孔隙度的增大，含水饱和度越大对纵波速度的影响越大，但是对横波基本没有太大的影响，这与横波参数不受孔隙流体的影响相符。因此，在利用Xu-White模型进行横波预测时，由于纵波速度是作为循环的收敛条件，固含水饱和度的影响基本不大。

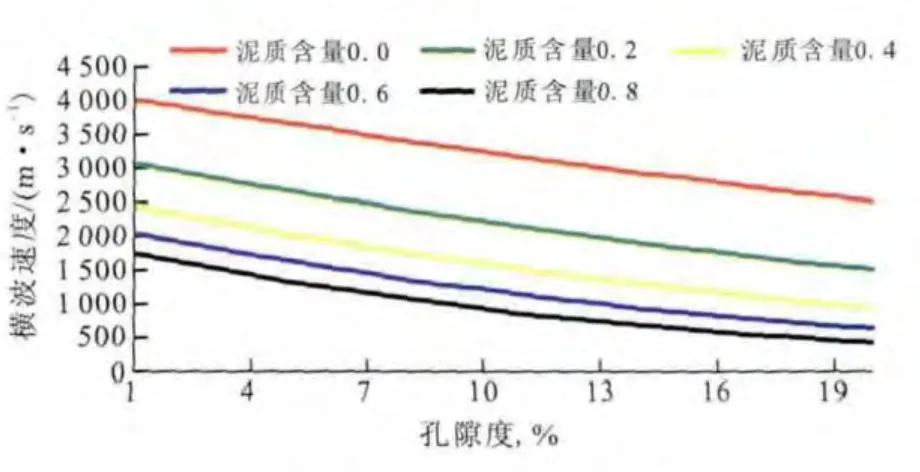
图2 泥质含量对横波速度的影响Fig.2 The effects of shale content on shear velocity

2.3 砂岩孔隙纵横比对纵横波速度的影响

针对砂岩孔隙度对纵横波速度的影响设计了一个饱含气水的砂泥岩模型3，含水饱和度20%，含气饱和度80%，泥质含量为20%，其它的详细参数见表2。

表2 模型3的岩石物理参数Table 2 Petrophysical parameters of model 3

试验中孔隙度的变化范围为1%～20%，取样间隔为1%，砂岩的孔隙纵横比变化范围为4%～12%，利用Xu-White模型计算不同砂岩孔隙纵横比情况下的纵横波速度，得到的纵波、横波速度随含水饱和度的变化情况（图5、图6）。

从图5和图6中可以看出：随着孔隙度的增大，砂岩孔隙纵横比对速度的影响呈现增大的趋势，这说明利用Xu-White模型进行横波预测时，如果砂岩孔隙纵横比取定值会产生很大的误差。这与Nur（1969），Brown（1975）对实验数据进行分析得到的结论是一致的，即岩石的孔隙纵横比不是定值。

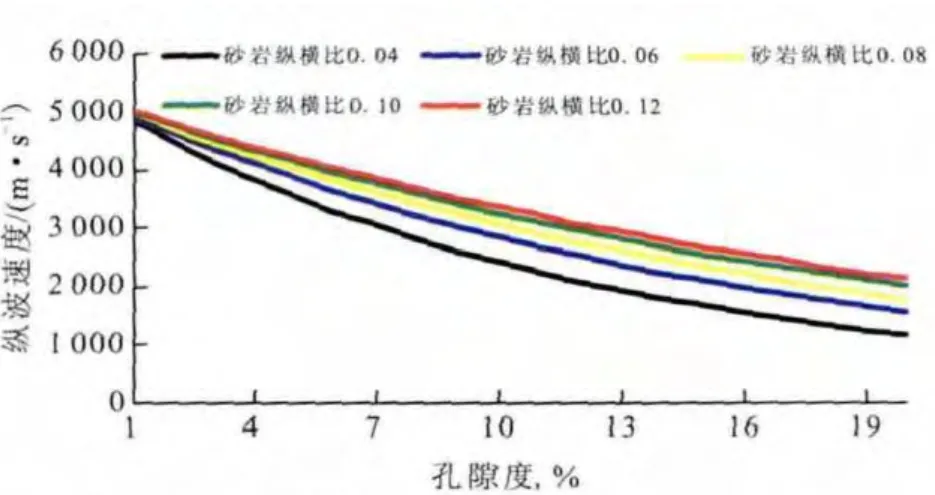
图5 砂岩孔隙纵横比对纵波速度的影响Fig.5 The effects of sandstone pore aspect ratio on longitudinal velocity

通过以上三个模型的试验，可以知道在运用改进的Xu-White模型方法预测横波曲线时，影响的权重由高到低依次为泥质含量、砂岩孔隙纵横比、含水饱和度。为了提高横波预测的精度，应首先尽量保证泥质含量的准确性，采用变化的孔隙纵横比[11]，应用岩石物理测试的经验公式加以条件限制，尽可能的使模拟的横波速度接近真实的速度。

3 实际应用

在参考了Castagna、Han等砂泥岩纵横波速度经验公式的基础上，运用校正后的泥质含量曲线，采用变化的孔隙纵横比对研究区的一口已有横波数据的井进行改进的Xu-White模型横波预测。具体的预测效果如图7所示。

图7中，第一道蓝色曲线为纵波速度，第二道蓝色曲线为实测的横波速度，粉红色曲线为预测的横波速度，第三道为密度曲线，第四道为校正过后的泥质含量曲线。从图中可以看出：预测的横波与实测的横波吻合度较高，证明改进的Xu-White模型能够很好的运用于研究区。

4 结论和讨论

利用Xu-White模型进行横波预测时会产生误差，该文就泥质含量、砂岩孔隙度和含水饱和度对预测的影响建立相应的模型，然后分析误差产生的权重，得到运用Xu-White模型预测影响权重最大的是泥质含量，其次为孔隙纵横比，含水饱和度对预测的影响不大。

针对产生误差的原因，采用校正后的泥质含量曲线，变化的孔隙度可以提高预测的准确性，在实际资料的处理中应用效果不错，估算的结果与实测的横波吻合良好。

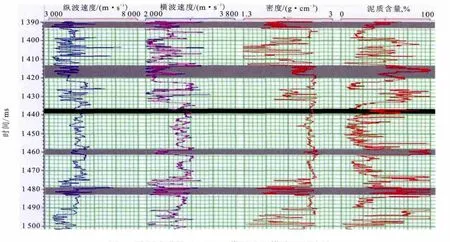
图7 采用改进的Xu-White模型进行横波预测效果Fig.7 Shear wave effect prediction by using improved Xu-White model

[1]曾忠玉,陈昭年,钟得盈,等.利用流体置换的Xu-White模型计算横波速度[J].新疆石油地质,2011,32（1）∶85-88

[2]孙福利,杨长春,麻三怀,等.横波速度预测方法[J].地球物理学进展,2008,23（2）∶470-474.

[3]葛瑞·马沃可,塔潘·木克基,杰克.德沃金.岩石物理手册——孔隙介质中地震分析工具[M].安徽∶中国科学技术大学出版社,2008.

[4]Han D H,Nur A,Morgan D.Effect of porosity and clay content on wave velocities in sandstones[J].Geophysics,1986,51(11)∶2 093-2 107.

[5]Castagna J P,Batzle M L,Eastwood R L.Relationships between compressional-wave and shear-wave velocities in clastic silicate rocks[J].Geophysics,1985,50(4)∶571-581.

[6]Xu S Y,White R E.A new velocity model for clay-sand mixture[J].Geophysical Prospecting,1995,43(1)∶91-118.

[7]Keys R G,Xu S Y.An approximation for the Xu-White velocity model[J].Geophysics,2002,67(5)∶1 406-1 414.

[8]李维新,王红,姚振兴,等.基于约束条件横波速度反演和流体替代[J].地球物理学报,2009,52（3）∶785-791.

[9]熊晓军,林凯,贺振华.基于等效弹性模量反演的横波速度预测方法[J].石油地球物理勘探,2012,47（5）∶723-727.

[10]陈颙,黄庭芳,刘恩儒.岩石物理学[M].安徽∶中国科学技术大学出版社,2009.

[11]白俊雨,宋志翔,苏凌,等.基于Xu-White模型横波速度预测的误差分析[J].地球物理学报,2012,55（2）∶589-595.