等效渗透率在底水油藏水平井数值模拟中的应用
2014-07-05魏敬超李立峰
程 强,魏敬超,李立峰
(1.中国石化江苏油田试采一厂,江苏 扬州 225265;2.中国石化江苏油田钻井处,江苏 扬州 225261)
利用水平井开采底水油藏,井筒内压力损失影响不可忽视[1-2]。由于油藏与井筒内流体流动规律不同,因此,在考虑井筒压降研究中,需要建立油藏渗流与井筒管流的耦合模型[3]。一些学者基于耦合模型研究了井筒内压力损失对水平井产能[4]、见水时间等的影响[5],还有学者研究了基于耦合模型的底水油藏水平井的数值模拟方法[6]。由于井筒与油藏的控制方程不同,耦合模型的求解难度较大,这对于大尺度的油藏数值模拟是非常不利的[7]。有学者在水利学研究中提出了水平井等效渗透率的概念[8],本文借鉴这种思路,推导了两相流动条件下等效渗透率数学表达式,统一了井筒与油藏中的控制方程,研究了等效渗透率在底水油藏水平井数值模拟中的应用。
1 物理模型与假设
底水油藏水平井开采物理模型如图1所示,油藏顶部为不渗透边界,底部为底水,保持定压,水平井定流量生产,本文研究考虑油水的界面张力与重力,忽略岩心与流体的压缩性。研究中的参数有:油层厚度h,m;储层渗透率K,m2;储层孔隙度Φ,无量纲;水平井长度L,m;水平井距底水高度Zw,m;原油密度ρo,kg/m3;地层水密度ρw,kg/m3;重力加速度g,m/s2;原油渗流速度vo,m/s;地层水渗流速度vw,m/s;油相黏度μo,Pa·s;水相黏度μw,Pa·s;油相饱和度So,无量纲;水相饱和度Sw,无量纲;油相压力po,Pa;水相压力pw,Pa;水平井产量Q,m3/s;含水率fw,无量纲。

图1 底水油藏水平井开采示意图Fig.1 Horizontal well exploitation diagram of bottom water reservoir
1.1 水平井筒的等效渗透率
水平井筒内压力损失有摩擦压降、加速压降与混合压降等。根据质量守恒与动量守恒,可以推导出水平井任意微元段压降数学表达式,如公式(1)所示:
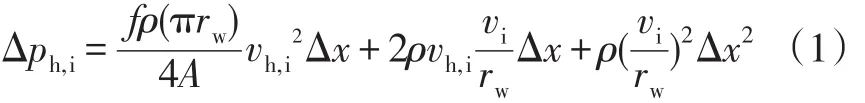
式中:Δph,i为任意微元段上压力损失;vh,i为井筒内流动速度;vi为油藏流体向水平井筒流入速度;A为水平井筒截面积,m2;rw水平井筒半径,m;f水平井筒摩擦系数,无量纲。公式(1)右侧第一项为摩擦压力损失,第二项与第三项为加速压力损失。有实验研究指出[9],摩擦压降约占全部压降的80%,因此公式(1)可以改写为:
由公式(2)可以得到井筒内流速与压力损失的关系:

将井筒内等效渗透率定义为∶

两相流动中,等效渗透率中参数随油水饱和度变化。根据质量平均,混合密度定义为∶
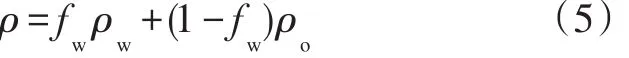
Sw为含水饱和度,So为含油饱和度,混合黏度定义[11]为∶

摩擦系数f计算方法受流态控制影响,流态与流动雷诺数Re有关,Re=ρvd/μ,当流动为层流,摩擦系数的计算公式为f=64/Re。当流动为紊流,摩擦系数的计算随雷诺数变化分为四个阶段,文献[10]中有详细的计算公式。
混合流速的计算公式为:

混合流速既是需要求解的未知量,同时又是计算等效渗透率所需的参数。因此,在数值模拟中需要对混合流速进行处理。在初始时刻,假设井筒内流态为层流,这种情况下,等效渗透率数学表达式中流速被约去,利用其他参数可以计算出一个初始的等效渗透率,并利用这个等效渗透率求解方程组,可以得到速度与压力分布,然后将新计算出的流速传递到下一时间步长中,用以计算下一时间步长内的等效渗透率,在之后时间步长中,采用相同的方法处理井筒内流速与等效渗透率。
将等效渗透率代入公式(3)后,可以得到井筒内流速与压力梯度关系,改写成微分形式后为∶

1.2 油藏与井筒的控制方程
可以看出公式(8)与达西定律形式相同,因此,基于等效渗透率,井筒中可以建立与油藏形式相同的运动方程。所以在数值模拟中,将水平井筒处理为油藏的一部分。油藏与井筒中油水相控制方程为:

式中:∇为梯度算子,krw为水相相对渗透率,kro为油相相对渗透率,D为海拔标高,m。补充方程为:

式中:pc为毛管力,po为油相压力,pw为水相压力。边界条件为:

根据补充方程,方程(9)可以变为:

公式(10)与公式(11)相加得到:

已知毛管力是含水饱和度的函数,在水驱油过程中含水饱和度随距离变化:
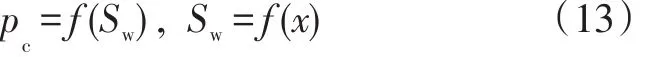
带入公式(12)可以得到:
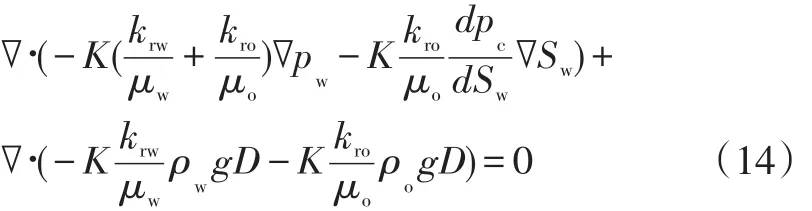
公式(14)为两相流动的压力微分方程,公式(10)为饱和度微分方程,加上边界条件就组成油藏与井筒内两相流动的数学模型。
在本文的模型中,水平井被当做油藏处理,所以需要赋予孔隙度、相对渗透率等参数。水平井孔隙度设置为100%,相渗关系设置为:

在水平井筒中不考虑毛管力,因此,油相压力与水相压力相同。
2 应用与讨论
在商业数值计算软件中建立物理模型,其中将水平井处理为油藏的一部分,分别赋予油藏和水平井不同的物性参数,输入文中推导的数学方程,通过编程处理等效渗透率,求解后就可以实现考虑井筒压降的底水油藏水平井数值模拟。
为验证本文方法的可靠性,利用该方法模拟了某底水油藏水平井开采实验过程。物理模型中模拟油藏的岩心的尺寸为80 cm(长)×10 cm(高)×10 cm(宽)。水平井模型长为70 cm,井径为2 mm,置于油藏模型顶部。在水平井布置4个压力传感器,以测量井筒里压力损失,物理模型的基本参数如表1所示。物理模型中岩心的相渗关系如表2所示。

表1 物理模型的基础数据Table 1 Basic data of physical model

表2 油藏模型中油水相渗关系Table 2 Oil and water relative permeability of reservoir model
将数值模拟得到的水平井井筒内压力分布与实验结果对比,如图2所示。可以看出,数值模拟与实验结果符合较好,从水平井指端到跟端,井筒内压力逐渐降低,而且越靠近跟端,压力下降速度越快,这使得大部分井筒压降发生在靠近跟端的井筒中。数值模拟结果很好地反映了井筒压力损失特征。

图2 水平井筒内压力分布Fig.2 Pressure distribution of horizontal wellbore
数值模拟与实验得到的水平井开采动态对比如图3所示。实验中底水突破进入井筒时间早、含水上升时间快,含水率至90%时,采出程度尚不足25%。数值模拟与实验结果符合较好。这表明本文方法能够较好地模拟底水油藏水平井开采特征,可以用于此类情况的数值模拟。与耦合模型相比,本文方法模拟精度差距不大,但求解难度降低。
3 结论
1)利用等效渗透率,可以在水平井筒建立与油藏相同的运动方程,从而不必建立耦合模型,降低底水油藏水平井开采数值模拟的难度。
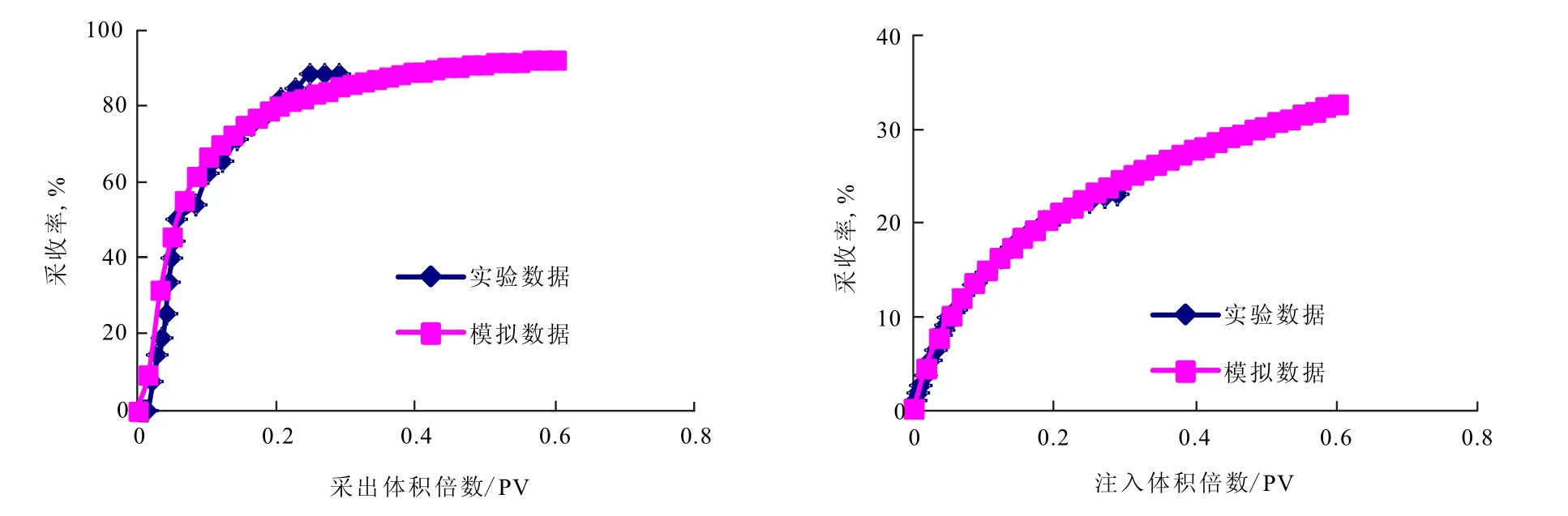
图3 水平井开采动态物理与数值模拟结果对比Fig.3 Result comparison of horizontal well exploitation and numerical simulation
2)基于等效渗透率的模拟与实验结果符合较好,能够用于考虑井筒压降的底水油藏水平井数值模拟。
[1]王家禄.水平井开采石油遇到的几个流体力学问题[J].力学与实践,2000,22(1)∶2-10.
[2]王小秋,汪志明,魏建光.井筒与油藏耦合条件下水平井变质量流运动规律研究[J].水动力学研究与进展,2005,20(3)∶326-331.
[3]Permadi P,Lee R L,Kartoatmodjo R S T,et al.Behavior of water cresting under horizontal wells[C].SPE 30743,1995∶431-439.
[4]刘想平,郭呈柱,蒋志祥.油层中渗流与水平井筒内流动的耦合模型[J].石油学报,1999,20(3)∶82-86.
[5]Umnuayponwiwat S,Ozkan E.Water and gas coning toward finite conductivity horizontal wells∶cone buildup and breakthrough[C].SPE 60308,2000.
[6]吴淑红,于立君,刘翔鹗,等.热采水平井变质量流与油藏渗流的耦合数值模拟[J].石油勘探与开发,2004,31(1)∶88-90.
[7]程林松,兰俊成.考虑水平井筒压力损失的数值模拟方法[J].石油学报,2002,23(1)∶67-71.
[8]陈崇希,万军伟.地下水平井流的模型及数值模拟方法——考虑井筒内不同流态[J].中国地质大学学报,2002,27(2)∶135-139.
[9]周生田.水平井变质量流研究进展[J].力学进展,2002,32(1)∶119-126.
[10]刘建军,章宝华.流体力学[M].北京∶北京大学出版社,2006.
[11]李宝柱,宋文杰,纪淑红,等.水平井水平段压力分布研究[J].石油学报,2003,24(2)∶97-100.
