OFDM系统时频二维信道估计研究*

范慧丽 许 建 任勤勇

(中国舰船研究设计中心 武汉 430064)

OFDM系统时频二维信道估计研究*

范慧丽 许 建 任勤勇

(中国舰船研究设计中心 武汉 430064)

针对短波信道时变色散的特点,设计了OFDM系统信道估计所需的时频二维棱形插入导频图案,并根据时频域两方向导频插入的稀疏程度,选择了二维插值的方法和插值次序,另外,提出了改进的变换域DFT信道估计算法。该算法通过适当选取变换域补零的位置,有效减小了非整数倍采样间隔信道时延引入的能量泄露,并滤除了噪声的影响。最后,在短波多径环境下仿真算法的性能,并与常用频域插值算法和维纳滤波方法进行了对比。仿真结果表明:改进方法的增强了算法对多径延迟分布的鲁棒性,提高了信道估计精度,同时还保持了较低的计算复杂度。

正交频分复用技术; 短波信道; 信道估计; 二维插值; 变换域DFT

Class Number TN915

1 引言

正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)技术可把频率选择性信道转换为多个平坦子信道,并利用循环前缀来避免符号间干扰,使得信道均衡变得非常简单,目前已经广泛应用于众多的高速数据传输领域[1～2]。

OFDM系统一般采用相干检测方法进行解码,这就要求获得准确的信道状态信息(CSI)。

基于导频辅助的信道估计由于具有简单、精确和高稳定性等特点,成为OFDM最常用的信道估计方式,其性能优于盲估计算法[3],通常采用块状、梳状、格形和菱形等四种导频模式。由于OFDM系统具有时、频二维的特点[4],所以基于二维模式的导频能更好地适应信道在时域和频域上的衰落,具有更低的导频密度和更高的频谱利用率[5]。

文献[6]指出二维信号处理情况下,采用棱形导频插入样式可以提高信道估计性能。本文以棱形导频为代表,对二维插值方法和插值顺序进行了研究,并对变换域插值的补零方法进行了改进,在短波多径环境下仿真算法的性能,并与常用的线性、二阶插值、三次条插值和维纳滤波方法进行了对比。仿真结果验证了改进方法的有效性。

2 OFDM系统模型

假设OFDM系统子载波总数为N,利用矩阵的表示形式,OFDM系统可表示为

Y=XH+W

(1)

式中Y为N×1的接收信号向量;X为N×N对角矩阵,对角线上的元素即为传送的导频和数据信号;W为一独立同分布的高斯噪声向量;H为信道的频域响应向量。其时域信道冲激响应(CIR)可以表示为

(2)

其中L为信道的多径数,αl和τl分别为第l条路径的信道增益和时延。

3 信道估计

3.1 导频分布模式

信道频率响应(Channel Frequency Response,CFR)可以看作是二维随机信号,因而在时频域插入导频实际上是对CFR的二维采样[7],那么插入的导频间隔就必须满足奈奎斯特采样定理以免发生频谱混叠。假设用τmax、fmax分别表示信道最大时延扩展和最大多普勒频移;Δf、Tsymbol分别为OFDM的载波间隔和符号周期。则在时间轴方向的归一化带宽为fmaxTsymbol,在频率轴方向的归一化带宽为τmaxΔf/2。因此时域、频域的奈奎斯特间隔Nf、Nt与信道的相关带宽、相关时间之间需满足:

Nt≤1/(2fmaxTsymbol)

(3)

Nf≤1/(2τmaxΔf)

(4)

由于Nf和Nt只能取整数,上面两式向上取整。

图1 导频位置分布图

本文所采用的棱形导频图案如图1所示,需要注意的是,图示中的导频结构在时间方向分布较密集,而在频率方向分布较稀疏,这是为了减少导频的数量,增大系统的频率利用率,虽然会增加整个信道估计的延迟,但实际上由于滤波器是线性的,在时频域两方向的导频间隔都满足奈奎斯特间隔时,不同的插值顺序(先时间方向后频率方向或是先频率方向后时间方向)可以得到同样的性能的。

3.2 二维插值顺序

从图1中可以看到,时间方向导频间隔Nt=3,根据式(3)可知,此时允许的最大多普勒频域扩展约为6Hz,足以满足短波信道模型的要求。另外,频率方向导频间隔Nf=6,同样根据式(4),可以算得此时允许的最大时延为1.7ms,适用于具有较小延迟扩展的短波信道,但是对较恶劣的信道,并不能满足采样定理。基于此,本文采用二维联合估计的方法,首先在时间方向进行插值,这样频域方向上的子载波间隔将由原来的6变为2,相应的最大可容忍时延也增大了3倍。再根据此时的插值结果,在频率方向上进行内插,最后就可以得到整个信道每个载频点上的信道响应估计值。图2给出插值顺序以及插值前后不同导频分布图。

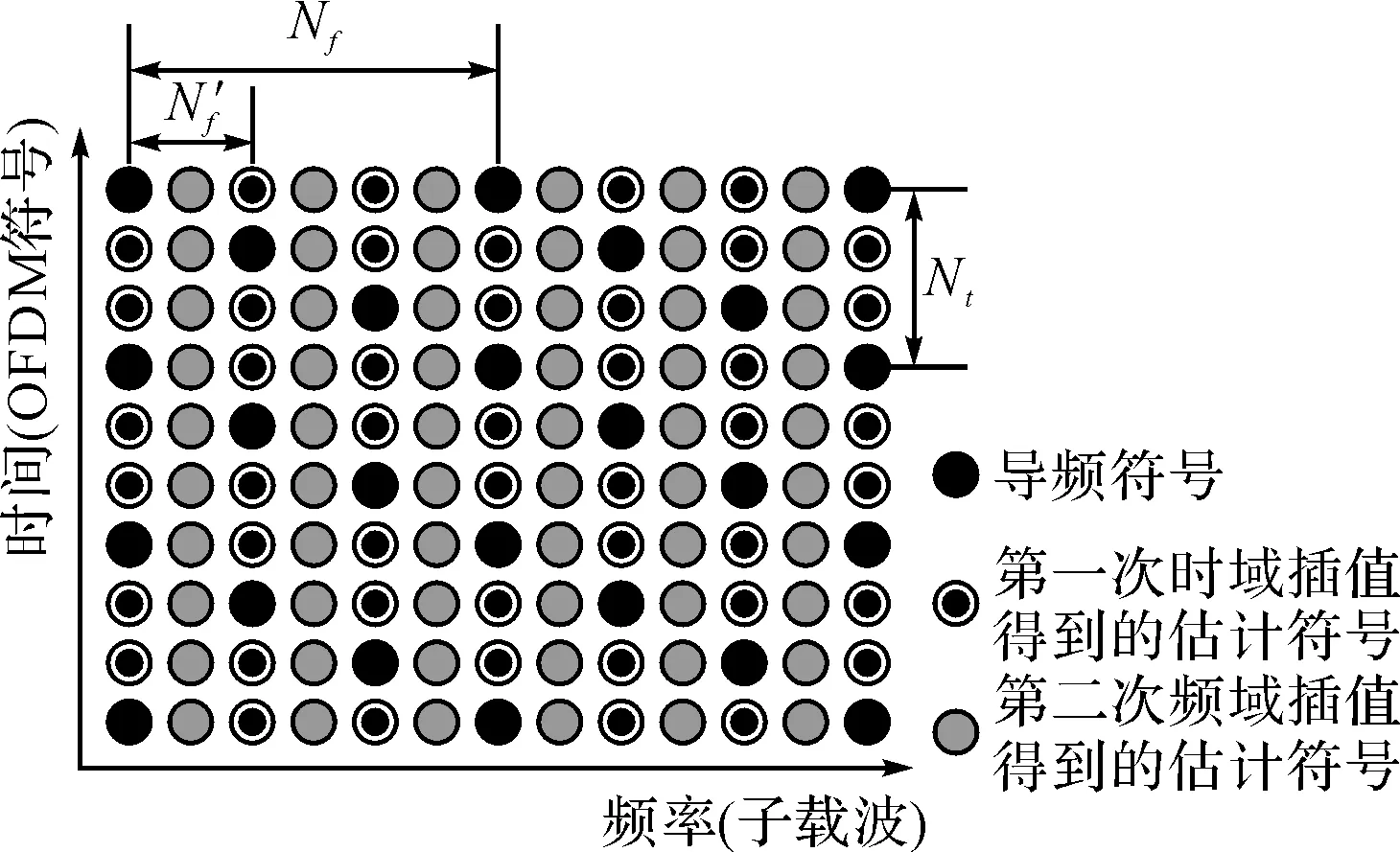
图2 时域插值前后的导频分布

3.3 基于变换域DFT信道估计方法

导频点处的信道估计可采用最小平方法(LS)、最小均方误差法(MMSE)等方法[8～9],LS估计性能虽不如MMSE,但其计算复杂度较低,适于实际工程实现。根据OFDM频域传输模型可知,导频点(p,q)处的信道频率响应的LS估计为

(5)

式中(lp,kq)表示导频在一帧OFDM符号内的位置。

为了得到所有子载波处的信道响应,必须对导频点信道响应值进行插值。常用的插值方法有线性、二阶、三次样条插值、变换域DFT以及维纳滤波等方法。本文主要研究变换域DFT补零信道估计方法。

根据补零位置的不同,有不同的DFT算法出现[10～11],但它们在非整数倍采样间隔信道中并不能有效地解决能量泄露问题,综合考虑其优缺点,这里提出一种折衷的补零方法,该算法在基本不增加复杂度的情况下可以有效地提高信道估计精度。假设一个OFDM符号内的导频数为Np,基于尾部补零和中间位置补零的补零起始位置分别为Np和Np/2,取其中间位置开始补零。首先根据导频估计出信道冲激响应,并设定一个门限值G,据此估计出信道的最大路径时延:

(6)

则补零的起始位置为

(7)

实际应用中,为了提高信道估计性能,导频数目Np通常以两倍过采样进行设置。因此,一般情况下导频数目Np都大于保护间隔长度Ng。另外,为了保证上一个符号的多径分量不会对下一个符号产生干扰,一般选择Ng>τmax,因此可采用更为简单的补零位置设置方法:

p=(Ng+Np)/2

(8)

可以看出,改进前的方法所确定的补零起始位置更确切,更贴合实际信道条件,当然是以增大计算复杂度为代价的,并且与所设定的门限值关系重大。

4 仿真结果与分析

为了进一步验证上述分析的正确性和改进方法的有效性,本节对所提的信道估计方法进行仿真。仿真中的信息比特采用(2,1,7)卷积码进行编码,调制方式采用QPSK调制,N=1024,Ng=256,Δf=48.83Hz;一帧信号包含十个OFDM符号,每一帧的第一个和最后一个OFDM符号内都包含了导频符号,同时使第一个子信道和最后一个子信道中也包含有导频符号,这样虽然增大了系统的冗余信息量,降低了系统效率,但是能保证每帧边缘的估计值更准确,提高了系统的估计性能。

仿真中采用了三种典型的短波多径信道模型[12],如表1。其中信道1为一个带有延迟路径的莱斯信道,在三个信道中最大时延最小。信道2和3是典型的CCIR Poor信道,为等幅多径信道,增大了多普勒扩展以及最大多径时延,主要用于验证二维采样间隔设置和内插顺序的可行性及不同二维插值方法的性能差异。

如前所述,所采用的棱形导频结构在时域方向导频间隔很小(即具有较高的过采样率),此时允许的最大多普勒频域扩展很大,完全满足给出的三种短波信道模型的要求,故对于时/频二维联合信道估计,在时域方向插值算法对系统性能影响并不是很大。而频率方向导频间隔很大,只能处理较小的延迟扩展(信道1),但是对较恶劣的信道(信道3),并不能满足采样定理要求,所以频域方向的插值算法对性能影响很大。

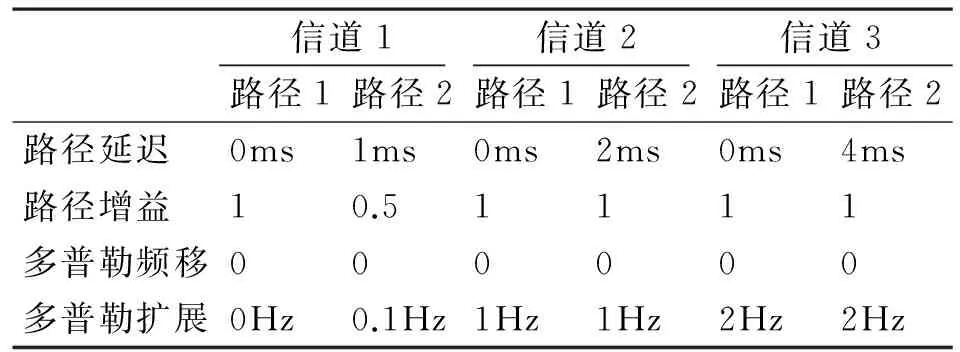
表1 仿真信道参数

图3和图4给出了不同信道条件下,二维时/频域联合插值和只运用一维频域插值算法的误码率性能。图中曲线标识只有一项的表示采用一维频域插值,有两项的表示二维联合插值,且前一项表示第一次在时域方向上的方法,后一项表示第二次在频域方向上的方法。可以看到,二维联合插值的效果明显优于一维频域插值,特别是在信道时延比较大的信道中(图4),此时,一维频域插值的性能急剧下降,基本不能估计出正确的信道响应。特别需要说明的是,图3中信噪比小于12dB时,二阶内插要劣于线性内插,三阶内插在信噪比下于8dB时也出现同样的现象,这主要是由于此时的信道为慢衰落信道,多阶内插在信噪比低时更容易跟踪噪声的变化而不是准恒定的信道传输函数,从而导致系统性能的下降。

图3 信道1条件下,不同信道估计方法的误码率性能

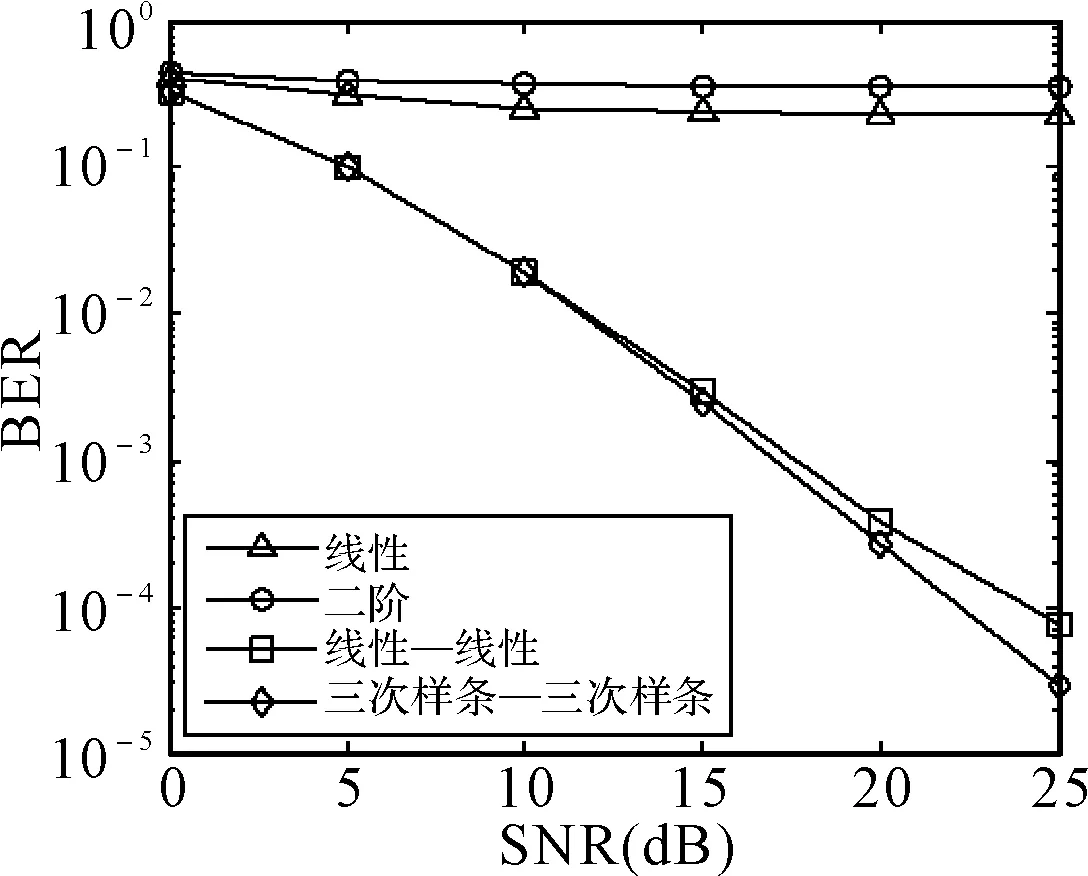
图4 信道2条件下,不同信道估计方法的误码率性能

图5和图6显示了信道2和3条件下,不同二维联合信道估计方法的误码率性能。由于时延相对较小,图5中的多条曲线都比较相近,也就是说采用不同算法的性能差异并不是很大,这与之前的分析是一致的。由于此棱形导频分布模式下,二维联合信道估计的性能主要取决于频域方向的估计算法,当时延扩展增大后(信道3),信道的频率选择性衰落更加严重,此时基于内插的算法的性能下降很严重,特别是线性内插算法,如图6所示。虽然三次样条插值可以得到较好的性能,但是在信噪比为25dB左右就达到了平底,性能难以提高。

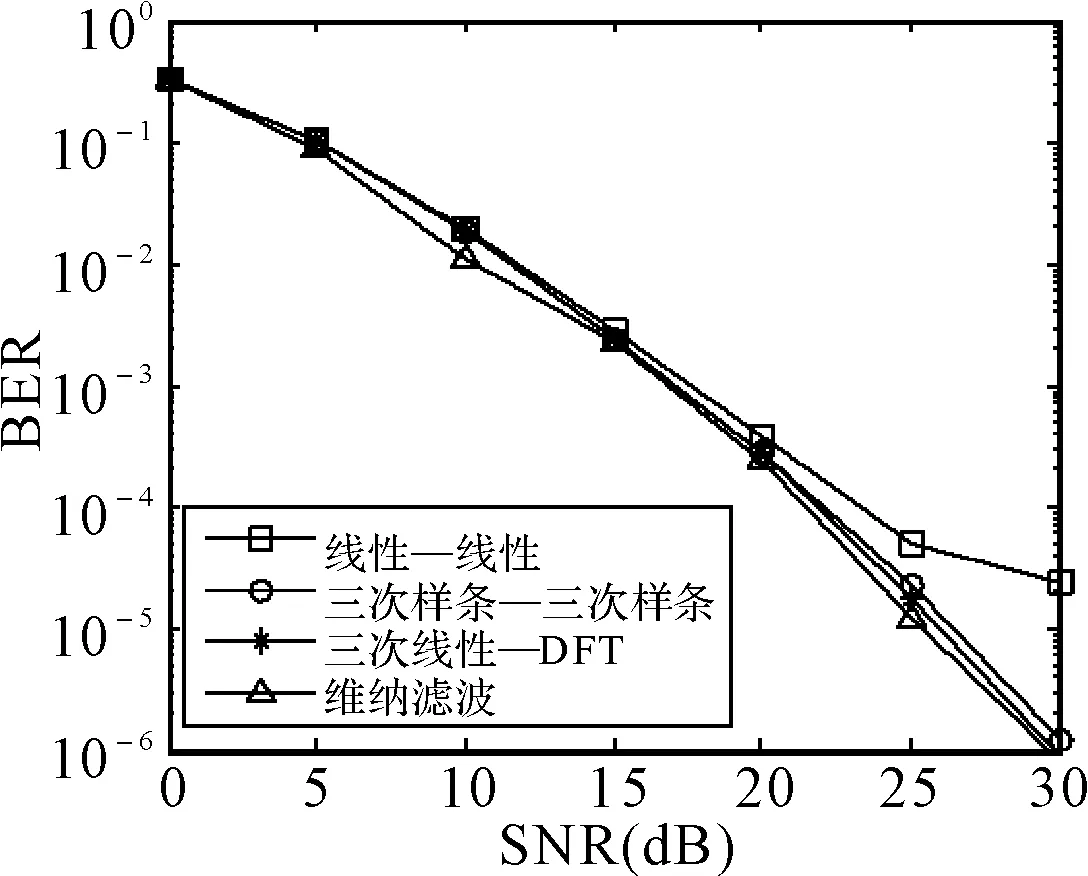
图5 信道2条件下,不同二维信道 估计方法的误码率性能

图6 信道3条件下,不同二维信道 估计方法的误码率性能

便于比较,图中还给出了均方误差最小准则下的最优估计方法性能—维纳滤波的方法。可以看到,基于改进的变换域DFT方法与维纳滤波方法性能上差别并不是很大,这是因为在变换域中进行低通滤波减小了子载波间干扰和高斯白噪声的影响,并且改进的DFT方法具有更低的复杂度,更适于工程实现。

5 结语

本文研究了短波信道下的OFDM二维信道估计方法,针对二维棱形导频插入模式,合适选择了插值的算法和次序,提出了基于变换域补零DFT的信道估计方法,并与经典的频域多阶插值算法及维纳滤波算法进行了详细的性能比较。仿真结果显示,改进的方法增强了算法对多径延迟分布的鲁棒性,具有较低的复杂度和较好的性能。

[1] Floch B L, Halbert-Lasalle R, Castellain D. Digital audio broadcasting to mobile receivers[J]. IEEE Transactions on Consumer Electronics,1989,35(3):493-503.

[2] Stuber G, Barry J, Mclaughlin S. Broadband MIMO OFDM wireless communications[J]. Proc. IEEE,2004,92(2):271-294.

[3] Del B V, Lavazza L. An empirical assessment of function point-like object-oriented metrics[C]//11thIEEE International Software Symposium,2005,54(1):124-127.

[4] Abran A, Robillard P N. Function points: a study of their measurement processes and scale transformations[J]. Systems Software,1994,25:171-184.

[5] Garmus D, Herron D. Function point analysis: measurement practices for successful software projects[R]. Addison-Wesley,2000.

[6] Jae Kyoung Moon, Song In Choi. Performance of channel estimation methods for OFDM systems in a multipath fading channels[J]. IEEE Transactions on Consumer Electronics,2008,46(1):161-170.

[7] LEE Shu-hong, HUNG Ho-lung, WEN Jyh-horng. A new interpolation method for channel estimation of OFDM systems[J]. TENCON 2005,2005,21(24):1-5.

[8] Speth M, Fechtel S A, Fock G, et al. Optimum receiver design for wireless broad-band systems using OFDM-Part Ⅰ[J]. IEEE Transactions on Consumer Electronics,1999,47(11):1668-1677.

[9] Jeon W G, Paik K H, Cho Y S. Two-dimensional MMSE channel estimation for OFDM systems with transmitter diversity[C]//Proceedings of the VTC 2001, Atlantic,2001,1:1682-1685.

[10] An C, Jang S, Lee J, et al. DFT-based Channel Estimation Using CIR Adaptation in OFDM Systems[C]//ICACT,2007,1:23-26.

[11] Zheng K, Su J, Wang W. DFT-based Channel Estimation in Comb-type Pilot-aided OFDM Systems with Virtual Carriers[C]//IEEE PIMRC,2007,1:1-5.

[12] CCIR. HF ionosphere channel simulators[C]//25th Plenary Assembly ITU, Dubrovnik, Ⅲ, rep.549-2,1986(3):59-67.

Time-frequency 2-D Channel Estimation Method for OFDM Systems

FAN Huili XU Jian REN Qinyong

(China Ship Development and Design Center, Wuhan 430064)

Aiming at the character of time-varying and dispersive HF channel, a time-frequency two-dimension diamond pilot pattern which is needed during OFDM channel estimation step, is designed. The two-dimension interpolation methods and order are chosen by the sparse degree of pilot in time domain and frequency domain. In addition, an improved channel estimation method based on transform domain DFT is proposed. The energy leakage of channel impulse response caused by non-integer-sample space can be decreased effectively by properly choosing the zero-padding position and the effect of noise can also be removed. Finally, simulation analysis and comparison of the algorithm with conventional frequency-domain interpolation and Wiener estimation approaches in shortwave multipath environment demonstrate that the improved algorithm improves the robustness for multipath delay, achieves channel estimation accuracy and ensures low complexity at the same time.

OFDM, shortwave channel, channel estimation, 2-D interpolation, transform-domain DFT

2013年8月7日,

2013年9月13日

范慧丽,女,博士研究生,研究方向:无线通信技术。许建,男,研究员,研究方向:舰船总体设计。任勤勇,男,高级工程师,研究方向:综合导航系统。

TN915

10.3969/j.issn1672-9730.2014.02.018