粒子滤波和无轨迹粒子滤波算法比较*

郑琛瑶 董真杰 张维全

(91388部队93分队 湛江 524022)

粒子滤波和无轨迹粒子滤波算法比较*

郑琛瑶 董真杰 张维全

(91388部队93分队 湛江 524022)

解决水下水声目标的定位跟踪问题,需要建立动态的非线性非高斯模型,粒子滤波直接采用未含有最新量测信息的状态转移先验分布函数作为重要性密度函数来逼近后验概率密度函数,无轨迹粒子滤波是在粒子滤波的过程中引入重采样技术,通过无轨迹变换设计重要性密度函数,使其更加接近系统状态后验概率密度。仿真结果表明粒子滤波和无轨迹粒子滤波算法都可以提高定位跟踪精度,但无轨迹粒子滤波算法的估计精度更高,更适用于工程实践。

无轨迹粒子滤波; 非线性非高斯; 重要性密度函数; 重采样; 定位跟踪

Class Number TP391

1 引言

水声目标的定位跟踪过程是一个动态的非线性、非高斯系统,对其仿真需要建立两个模型:系统模型(描述目标随时间而变化的状态)和测量模型(与目标状态有关且带有噪声),科学家研究出很多非线性滤波算法来解决这一问题,其中应用最普遍的是粒子滤波PF(Particle Filter)[1],PF算法对测量值进行数据融合,能够在一定程度上提升定位跟踪精度。而无轨迹粒子滤波UPF(Unscented Particle Filter)[2]是将PF算法做了改进,引入了重采样技术,能够获取更好的滤波性能。文章重点介绍两种算法在原理上的区别以及仿真所展示出的两者滤波性能的优劣。

2 PF算法的基本思想

PF算法采用序列蒙特卡洛的方法来解决非线性非高斯动态系统的状态递归估计问题,其核心思想是用一组加权随机样本(粒子)来近似表征后验概率密度函数[3～4],PF算法的基础是序列重要性采样SIS(Sequential Importance Sampling)。基于SIS的PF算法潜在的问题是样本退化(Degeneracy),就是在滤波过程中经过几次迭代,除了一个样本外其余样本的重要性权值都很小,结果粒子集无法表达实际的后验概率分布。为了解决样本退化问题,引入采样重要性重采样SIR(Sampling Importance Resampling),SIR的基本思想是通过在两次重要性采样之间增加重采样步骤,消除权值较小的样本,复制权值较大的样本,产生的粒子是独立同分布的,所以权值都设定为1/N,最常用且具有代表性的重采样有多项式重采样、层重采样、系统重采样和剩余重采样。重采样操作旨在缓解权值退化问题,增加样本多样性,但是同时也增大了计算量。

3 UPF算法的原理

研究机动目标定位跟踪,首先要建立动态状态空间模型[5]离散型式可表示为

(1)

UPF是利用无轨迹卡尔曼滤波UKF(Unsented Kalman Filter)方法来生成下一个预测粒子,由于充分考虑了最新的观测值,从而提高了估计精度。其基本思想是在使用无轨迹变换的基础上,加入了最新的观测量并产生非线性粒子滤波的建议分布:

(2)

基本算法步骤如下:

第六步:判断算法是否结束,若是则退出本算法,否则令x=k+1,返回第二步,递推下一时刻的后验概率。

4 PF与UPF的算法比较

PF算法主要存在两个缺点:粒子退化和粒子贫化[6]。前者是由于从重要性密度函数中取得的样本并没有考虑当前的量测值,导致与真实样本的偏差较大,当重要性权重的方差不断递增,粒子的权重集中到少数粒子上,造成大量计算浪费在对估计不起作用的粒子上,这就是粒子退化问题；后者是由于为了克服退化问题,采用重采样技术,复制大权值粒子,删除小权值粒子所产生的粒子贫化问题。PF和UPF算法过程可以用图1和图2所示的流程图展示。可见UPF算法是在PF算法的基础上增加了重采样过程,采用了含有当前最新量测数据的状态转移先验分布作为重要性密度函数,可以很好的逼近后验概率,尤其是当观测数据出现在转移概率分布的尾部或似然函数同转移概率分布相比过于集中时(如呈尖峰型)[7～10],PF算法可能失败,但是UPF算法能够解决这一问题。

图1 PF算法流程图

图2 UPF算法流程图

5 算法仿真

文章分别采用PF和UPF算法来进行目标的定位,将两个观测站获取的测量数据进行融合,通过一个非线性非高斯的例子来考察验证两种算法的性能,并且建立了系统动态方程。

观测模型:Zt=Xt+W

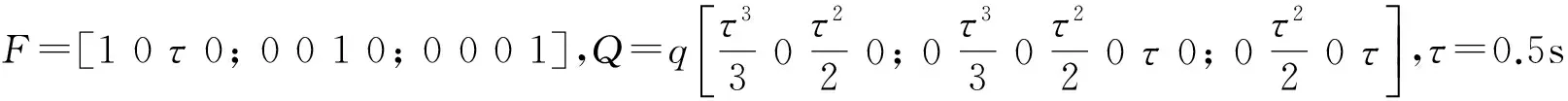
粒子数Ns=500,X0=[0 0 10 150]′,进行100次蒙特卡洛仿真,得到目标的位置估计、速度估计和均方误差,分别如图3～图5所示。

图3 UPF算法的位置估计

图4 UPF算法的速度估计

图5 UPF算法的均方误差

在与UPF同样的初始条件下,文章采用传统的PF算法也做了仿真,粒子数仍然是500,得到目标的位置估计、速度估计和均方误差,分别如图6～图8所示。

图6 PF算法的位置估计

图7 PF算法的速度估计

图8 PF算法的均方误差

比较图3和图6可以看出,UPF算法位置估计与目标真实轨迹更接近,比PF算法的位置估计效果更好。

比较图4和图7可以看出,UPF算法速度估计在X方向和Y方向均表现的更平稳,比PF算法的速度估计效果更好。

比较图5和图8可以看出,UPF算法均方误差估计在100次仿真中比较平稳,绝大部分数值都落在100m以内,而PF算法的均方误差估计值30次循环时就达到最低,之后发散,不够平稳,因此UPF算法的均方误差效果更好。

6 结语

UPF算法通过生成较好重要性密度函数,采用重采样技术,在一定程度上抑制了粒子退化现象,但重采样也带来了新的问题,即粒子贫化。由于较大权值的粒子被多次选择,较小权值粒子被剔除,使得采样结果中包含许多重复点,降低了粒子的多样性。采用UPF算法进行目标定位跟踪,比PF算法表现更优,因此在工程实践中往往选择UPF算法来对测量值作数据融合,达到提高精度的目的。

[1] Carpenter J, Clifford P, Fearnhead P. Improved particle for nonlinear problem[J]. IEEE Proceedings of Radar Sonar Navigation,1999,146(1):1-7.

[2] Zhan Ronghui. Modified unscented particle filter for nonlinear Bayesian tracking[J]. Journal of Systems Engineering and Electronics,2008,19(1):7-14.

[3] 王婷婷,郭圣权.粒子滤波算法的综述[J].仪表技术,2009,6(3):64-66.

[4] 王宁.基于高斯厄米粒子滤波的红外点目标跟踪算法研究[D].南京:南京航空航天大学,2007.

[5] 孙枫,唐李军.Cubature粒子滤波[J].系统工程与电子技术,2011,33(11):2554-2557.

[6] 梁磊,逄博,等.基于基于人工鱼群的无轨迹粒子滤波算法[J].计算机应用与软件,2012,29(1):140.

[7] Rolf H Reichle. et. Extended versus Ensemble Kalman Filtering for Land Date Assimilation[J]. American Meteorological Society,2010,3(6):728-740.

[8] Fabien Campillo, Rivo Rakotozafy. Parallel and interacting Markov chain Monte Carlo algorithm[J]. Elsevier Science Publishers B.V.,2009:3424-3433.

[9] Adam M Johansen. A note on auxiliary particle filters[J]. Statistic & Probability Letters,2008,78(2):1498-1504.

[10] Chen Shuiying, Zhang Jianyun.裂变自举粒子滤波[J]. Acta Electronica Sinica,2008,36(3):500-50.

Comparison of Particle Filter and Unscented Particle Filter Algorithms

ZHENG Chenyao DONG Zhenjie ZHANG Weiquan

(Unit 93, No. 91388 Troops of PLA, Zhanjiang 524022)

To resolve the underwater acoustic position precision and tracking, this paper establishes a dynamic nonlinear non-Gaussian model. The particle filter directly employs the state transition prior distribution function which does not include the latest measuring information as an importance density function to approximate the posterior density function. The unscented paticle filter brings in resampling technique, develops the importance density function by unscented transformation that is more close to the posterior density. Simulation results demonstrate that paticle filter and unscented paticle filter all can increase the precision of target position and tracking, but there is higher estimation precision with the latter. The algorithm of unscented paticle filter is more suitable for engineering pactice.

unscented particle filter, nonlinear non-gaussian, importance density function, resampling, position precision and tracking

2014年6月6日,

2014年7月27日 基金项目:国家自然科学基金重点项目“基于联合决策与估计的高频超视距雷达信息处理与融合”(编号:61135001)资助。作者简介:郑琛瑶,女,硕士研究生,助理工程师,研究方向:水声信号处理研究。

TP391

10.3969/j.issn1672-9730.2014.12.012