Simulink在“通信原理”研究型教学中的应用

党小宇，刘兆彤

(南京航空航天大学电子信息工程学院，江苏南京210016)

0 引言

“通信原理”是电子信息工程专业的一门重要专业基础课程，它以“概率论与数理统计”等相关课程为基础，也是后续专业课程如“移动通信”等的基础，所以其在通信专业的学习中启着承上起下的作用，故其教学方法显得十分重要。这门课程的特点是数学推导多，公式复杂，知识面广，都使得学生在学习这门课程时感到吃力。

在“通信原理”这类专业课的学习过程中，复杂的公式和过多的概念会僵化学生的思维，而研究型教学可以激发学生探索问题的积极性，从而提高学习效率[1]。

传统的“通信原理”课程的研究型教学多是采用硬件实验的方法，需要昂贵的实验设备仍无法完全满足课程演示和实验的需要[2]。虽然采用Matlab编码作为辅助教学工具可加深学生对该课程的理解，但是用代码编程的方法也有其局限性。“通信原理”课程的重要部分在调制和解调章节，而Matlab代码中比如码元速率，载波频率等诸多参数均需经过计算再设置。而且学生需要经过一段时间的学习才能熟练掌握指令。所以寻找一种易于学习且参数设置比较直观的研究型教学方法显得尤为重要。

Simulink中模块化的图形界面上可以实现相应的模型构建，各个模块的参数也只需在图形界面上设置，使得设计过程简单直观且易于掌握，学生借助它可以迅速独立完成一些简单的系统设计，有助于提高学生自主学习和探索创新的积极性。

本文以调制方式为例，在对“通信原理”课程中已介绍的MSK调制方式进行学习和研究的基础上，研究一种用于UHF卫星通信的SBPSK(Shaped Binary Phase Shift Keying)调制，并通过Simulink搭建调制模型，探索并总结出SBPSK调制的特性[3]。

1 基于Simulink的MSK的理论验证

1.1 MSK主要设计步骤

MSK(最小移频键控)是一种连续相位调制，其等价基带模型的表达式为

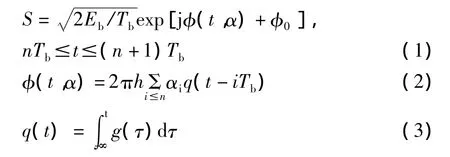
MSK主要设计步骤可以概括为以下几步:①对将产生的‘0’和‘1’序列进行‘1’和‘-1’映射;②对码元进行采样，设置一个码元采样10个点;③用成形函数g(t)=1/2Tb(0≤t≤Tb)，对其滤波;④对经过成形函数滤波过的输出码元进行积分;⑤将积分结果乘以2πh，这里h=0.5，就可得到基带相位特性的变化，观察基带MSK信号频谱。

1.2 MSK调制的Simulink设计

MSK调制的Simulink设计如图1所示。

图1 MSK调制的Simulink设计

MSK调制主要模块主要包括:

(1)码元速率设为100k，采样率设置为1e6。理想矩形脉冲滤波器(Ideal Rectangular Pulse Filter)模块用来实现对一个码元采样10个点;

(2)乘法器 Product2，Product3，减法器 Substract，常数 Constant3，Constant4，Constant5 模块用来实现‘0’，‘1’序列到‘1’，‘-1’序列的映射;

(3)常数Constant和乘法器Product4模块用来实现成形函数的归一化;

(4)离散时间积分器(Discrete-Time Integrator)模块用来实现积分。

1.3 MSK调制实验结果及分析

将MSK信号的基带频谱与常用的BPSK信号基带频谱进行比较，观察MSK频谱的特性并验证，如图2所示。

图2 MSK与BPSK基带频谱的比较

图中的CH1代表MSK信号的基带频谱，CH2代表BPSK信号的基带频谱。与BPSK相比，MSK第一个零点出现在0.75/Ts(Ts为码元周期，这里设为1e－5)，即75kHz处，而BPSK的第一个零点出现在1/Ts即100kHz处。从而表明MSK信号的功率谱的主瓣所占的频带宽度比BPSK信号的窄，而且MSK的功率谱的旁瓣衰减速比BPSK更为迅速。这些结论与“通信原理”课程中已知的结论相符，从而验证了MSK信号的频谱特性。

MSK基带相位特性的变化如图3所示。为方便观察，这里设置显示10个码元的相位变化。

由图中可以看出，当输入的经过成形函数后的码元ai为1时，MSK相位增加π/2，当输入码元ai为－1时，MSK相位减少π/2，相位变化的持续时间都为一个码元周期，与已知结论相符，从而也验证了MSK的相位特性。

通过本实验可以看出在已知MSK理论基础的情况下，用Simulink可以方便的搭建模型进而实现理论验证，省去了编程计算和硬件搭建实现的麻烦。

图3 MSK信号的相位变化

2 SBPSK调制特性

2.1 SBPSK调制的概念

通过Simulink对MSK调制的模型搭建，学生对其特性进一步熟悉，在这基础上可以主动去研究探索新的调制方式和特性。SBPSK作为一种新的调制方式，其参考文献较少，学生对其特性也不熟悉。这就要求他们在知道SBPSK调制方法的基础上，自己尝试搭建SBPSK的调制模型，再根据仿真结果来研究和总结SBPSK调制方式的特性。

SBPSK的调制方式与MSK相似，其等价基带模型表达式与MSK一样[5]。但有如下不同点:

(1)SBPSK的成形函数又称成形录数(Shape Factor)，表达式为

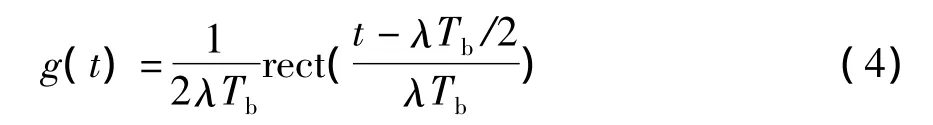
本文使用的是λ=0.5的SBPSK调制，即成形函数宽度设置为半个码元周期，幅度设置为1/Tb(Tb是码元周期)。

(2)SBPSK的调制指数h=1，MSK是h=0.5。

(3)SBPSK调制的码元之间存在一定的差分关系，为了便于说明，本文采用差分公式实现:

式中，ai，ai－1，ai－2均为‘1’，‘-1’序列。

由此可知，SBPSK的设计只需要根据以上三点差异对MSK的调制进行修改即可。

2.2 SBPSK的Simulink设计

SBPSK调制的Simulink设计如图4所示。如上所述，SBPSK的调制模型的搭建步骤与MSK基本相同，码元速率同样设为100kb/s，采样率设置为1e6。只是需要增加部分模块和修改部分参数即可。主要有如下设计模块。

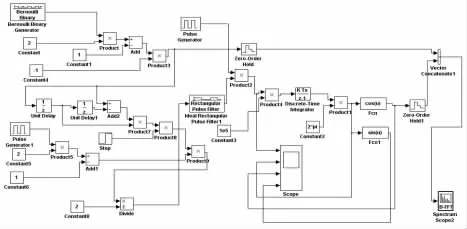
图4 SBPSK的Simulink设计

(1)单位延时Unit Delay和Unit Delay1模块用来实现码元延迟，获取 ai－1，ai－2。图中的加法器Add1，Add2，乘法器 Product5，Product7，Product8 和Product9，脉冲信号产生器Pulse Generator1，常数Constant5，Constant6，Constant8，阶跃信号产生器Step和除法器Divide等模块用来实现αi=(-1)i+1ai－1(ai－ ai－2)/2 变换。

(2)脉冲信号产生器Pulse Generator模块用来形成半个码元宽度的成形函数。

2.3 SBPSK调制实验结果及分析

将SBPSK信号的基带频谱与常用的BPSK信号的基带频谱进行比较，其频谱特性如图5所示。

图5 SBPSK与BPSK基带频谱比较

图5所示的CH1表示BPSK信号的基带频谱，CH2代表50%SBPSK信号基带频谱。在相同的码元速率下，SBPSK与BPSK的主瓣基本相同，第一个零点都出现在1/Ts即100kHz，但是其旁瓣衰减比BPSK要快。所以成形函数g(t)的引入在保留了主瓣的特性基本不变的同时，加速了SBPSK旁瓣的衰减。

SBPSK的相位变化特性如图6所示。为了便于观察，这里设置显示10个码元的相位变化。从图中可以看出SBPSK相位变化的特性:若经过成形函数后的码元ai前半周期为+1时，SBPSK相位增加π，相位变化的持续时间是半个码元周期;若码元ai前半周期为-1时，其相位减少π，相位变化的持续时间也是半个码元周期;码元为0时其相位不变。

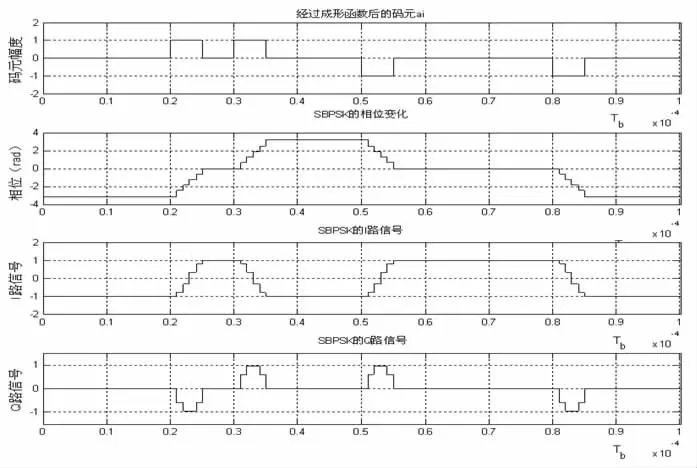
图6 SBPSK的相位变化

我们通过在MSK基础上搭建SBPSK基带调制系统进而研究其特性的实验可以发现，Simulink不仅可以用来验证一些已有的结论，还可以方便的用来研究新的调制方式的相关特性，避免了传统使用硬件实验进行验证和探索的麻烦。

3 结语

本文通过介绍利用Simulink在MSK调制的基础上尝试搭建一种新的调制SBPSK的模型，进而对其特性进行研究的实验证明了基于Simulink的研究型教学的方法具有快速入门，设计界面直观的优点，同时也省去了编程计算和硬件实现的麻烦，在方便了研究型教学的同时也提高了学生自主学习和创新的积极性。基于Simulink的研究型教学的方法已经在我校“通信原理”课程中使用并已取得了良好的效果。

[1]汪霞.大学研究型教学中的“研究”[J].上海.教育发展研究，2007(11B):43－46.

[2]张晶，李心广.MATLAB在通信原理教学中的应用[J].北京.中国现代教育装备，2007(2):21－23.

[3]Belkerdid M.A.，Mears T.J.，Weeter H.T.UHF SATCOM Adjacent Channel Emissions and Modem Implementation Loss:Predictions/Measurements for the Linear Phase SBPSK Modulation Waveform Family[C].Baltimore.Military Communications Conference，2005.

[4]邓红涛，查志华，张锐敏.Simulink在通信原理教学中的综合应用[J].石家庄.教育教学论坛，2012(3):211－212.

[5]Fox M.E.，Marcellin M.W.Shaped BPSK and the 5 KHz UHF Satcom Channels[C].Baltimore .Military Communications Conference，1991.