基于SIFT的图像匹配算法

周丽芬

(曲靖师范学院计算机科学与工程学院，云南 曲靖 655011)

0 引言

图像匹配是计算机视觉和图像处理领域中的一个重要研究方向，它是许多其它应用的重要基础，如图像识别、图像检索、目标跟踪、数据挖掘和3D重建等[1]。图像匹配算法大体上可分为2种:基于全局特征的匹配算法和基于局部特征的匹配算法[2]。由于局部特征只与特征点周围局部区域有关，所以基于局部特征的匹配算法更加稳定。目前广泛应用的基于局部特征的提取算法是Lowe提出的尺度不变特征变换 SIFT(Scale-Invariant Feature Transform)算法[1]，由于该算法的优越性，现在已经广泛应用于计算机视觉的各个领域。

随后出现了基于SIFT算法的很多改进算法，例如 PCA-SIFT[3]、 SURF[4]、 GSIFT[5]、 CSIFT[6]、ASIFT[7]等。文献[2]中，作者对这几种算法进行了详细的分析与比较，把不同算法应用于各种图像，评价各算法对尺度和旋转、光照、模糊、仿射等不变性的能力，作者将评价等级分为3种等级，依次是:Good，Better，Best。利用SIFT算法提取特征对模糊图像进行匹配的最终评价是Good。国内学者也对SIFT算法进行了改进，文献[8-9]等对SIFT算法的改进基本都是针对描述子部分，改变了关键点局部区域的结构或者简化了描述子构造，虽然在某些情况比原始算法效果要好，但是由于描述子的改变可能会使得算法对于其它情况的效果并不理想。近年来也出现了一些新的描述子，如文献[10-12]等，它们尽管效果很好，但是由于计算复杂度较高，描述子维数较高且结构较复杂，所以使用价值有待提高。

实验中发现，当要匹配的图像比较模糊时，利用SIFT算法提取的关键点较少，导致匹配时正确匹配率不高。针对这种情况，本文提出基于SIFT的针对模糊图像匹配增强算法，首先利用增强算子对图像进行锐化处理，使其边缘得到突出，再利用算法进行关键点提取。这样的操作使获得的关键点数量比直接利用SIFT算法有大幅度提高。当然关键点数量多并不意味着匹配效果一定好，因为关键点增多，误匹配率也会增大。因此为了提高匹配率，利用双向匹配算法[13]来删除错误匹配，从而提高匹配精度。

1 SIFT算法

基本的SIFT算法包括4个步骤:1)构造高斯差分金字塔;2)检测极值点;3)为关键点分配方向;4)生成描述子。下面简要介绍SIFT算法。

1.1 构造高斯差分金字塔

首先建立多尺度空间，即高斯金字塔，通过将输入图像I(x，y)与不同尺度的高斯函数卷积得到高斯金字塔一组的每一层，然后由上一组尺度为2倍初始尺度的图像降采样得到下一组的第一层，按照上一组同样的方式得到各层，最终构造高斯金字塔。将高斯金字塔相邻2层相减得到高斯差分金字塔:

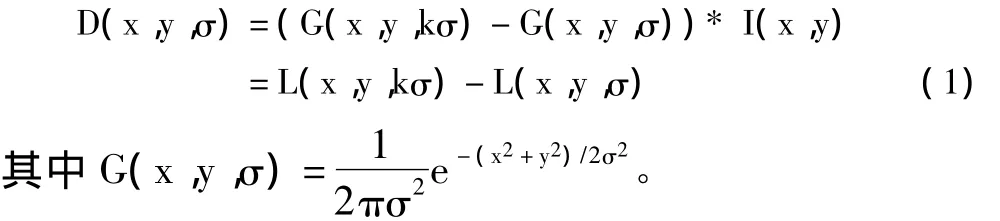
1.2 检测极值点

在高斯差分金字塔每组的第二层到倒数第二层检测极值点，所检测的点要与同一层周围8个点和上下2层该点周围的9×2个点比较，即总共与周围26个点进行比较，这样得到初步的极值点。再通过子像素插值精确定位极值点并删除对比度较低的极值点，剩下的极值点即为最终的关键点。

1.3 为关键点分配方向

利用关键点邻域像素的梯度方向分布特性为每一个关键点分配方向，使得算子具有旋转不变性。首先计算关键点处的梯度模值和方向。在以关键点为中心的邻域窗口内采样，并利用直方图统计邻域像素的梯度方向，直方图的峰值对应的度数代表了关键点的主方向。当存在超过主峰值80%的峰值时，其对应的方向作为该关键点的辅方向。

1.4 生成描述子

首先将坐标轴按照关键点的方向旋转，保证旋转不变性，然后以关键点为中心取16×16的窗口，分割成4×4的小区域，每个小区域上计算8个方向的梯度直方图，绘制每个梯度方向的累加值，就可形成一个种子点，因此总共有16个种子点，每个种子点由8个数字组成，所以最终形成了一个长度为128的向量，即为该关键点的SIFT特征向量。计算每一个关键点的SIFT特征向量，得到最终描述子，利用描述子可以进行匹配。

2 基于锐化的匹配算法

通过SIFT算法的原理和实验可以发现，SIFT算法检测到的许多关键点都是边缘点，然而由于在构造金字塔的时候会将图像经过多次高斯平滑，使得边缘点变得很平滑，如果所获取的图像本来就质量不高，直接利用SIFT算法提取关键点进行匹配，将会大大降低匹配精度。为了提高匹配率，本文提出先对图像进行锐化处理以提高SIFT提取的关键点数，再采用双向匹配算法进行匹配。

2.1 锐化算子

图像锐化处理的主要目的是突出图像灰度的过渡部分，即边缘，二阶微分是经常用来增强边缘的算子，其中拉普拉斯算子是最简单的各项同性微分算子[14]。一个图像函数f(x，y)的拉普拉斯算子定义为:

其中二阶导数计算的离散公式为:

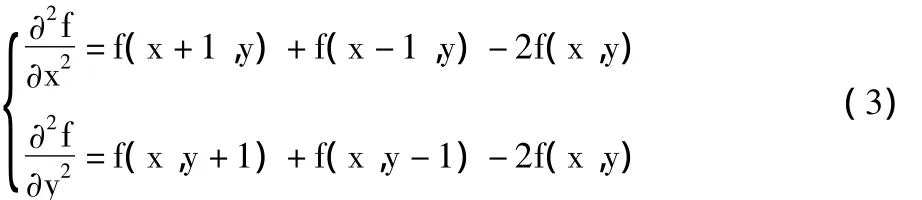
则拉普拉斯算子可表示为:

实际应用中，拉普拉斯算子可以通过下面的滤波模板来实现:

2.2 双向匹配算法

在文献[13]中，为了提高匹配精度，提出了双向匹配:利用SIFT算法进行特征提取，得到2幅待匹配图像的特征集，对第一个特征集中的每一个特征，在第二个特征集中计算最邻近距离和次邻近距离的比值(Ratio)，如果比值小于某阈值则匹配。这样经过第一轮匹配后，再在已匹配点中，对第二个特征集中的每一个特征，在第一个特征集中计算最邻近和次邻近距离的比值，如果比值小于某阈值则为匹配，当第二次匹配时，这样的关键点才规定为最终的匹配点。

在Lowe的算法中设定的阈值为Ratio=0.8，由于阈值设定得越小，匹配点数越少，阈值设定得越大，匹配点数越多，但是错误匹配也会增多。本文通过大量的实验，设定的2次阈值分别为Ratio1=0.8，Ratio2=0.5时效果较好。第一个阈值较大，这样可以得到较多的匹配点，第二个阈值较小，这样可以删除很多错误匹配，从而提高匹配精度。

2.3 本文算法

本文算法是在传统SIFT基础上增加图像锐化处理过程，并且在匹配时使用双向匹配算法。匹配算法步骤如下:

1)读入待匹配的2幅图像，将图像与拉普拉斯滤波模板卷积得到锐化后的图像;

A：根据十九大精神，我们企业已经进入了新的发展阶段。前些年我们已经着手进行了调整转型，现在需要在这个基础上进一步思考持续发展的问题。当前公司面临的任务是印刷产业的转型升级、环保治理，等等。我们认为，在新的形势下，二二〇七工厂，应当把服务首都功能和为军服务保障统一起来，这是企业持续发展的基础，是体现企业存在价值的重要方面。

2)使用传统SIFT对锐化后的图像进行特征提取，得到描述特征点的2个特征向量集;

3)使用双向匹配算法以欧氏距离为测度进行图像匹配。

3 实验结果与分析

为了验证该算法的优越性，进行了以下实验。实验平台:处理器为Intel(R)Pentium(R)CPU G620@2.60 GHz;内存为 4.00 GB(2.99 GB 可用);系统类型为32位Win7系统;软件为Matlab 2012a。

3.1 仿真实验

利用Cameraman的512×512的灰度图像，首先对其进行高斯平滑，得到平滑后的模糊图像，然后将平滑后的模糊图像与原图像进行匹配。采用以下3种匹配方式:

方式1:直接利用SIFT算法提取特征进行匹配;

方式2:先利用拉普拉斯算子对模糊图像锐化处理，再利用SIFT算子提取特征进行匹配;

方式3:首先利用拉普拉斯算子对模糊图像锐化处理，然后利用SIFT算子提取特征，最后利用双向匹配算法进行匹配。

由图1可以看出，在图1(a)中匹配点数不多，而且存在很多错误匹配;由于利用拉普拉斯算子锐化了模糊图像，所以图1(b)中匹配点数增多，但是错误匹配也会增多;如果利用双向匹配算法进行匹配可以在很大程度上删除错误匹配点，如图1(c)中错误匹配几乎没有，匹配点数也较多，所以匹配效果最好。

图1 3种方式匹配结果

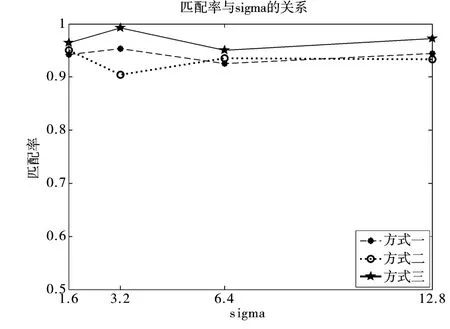
图2 不同sigma时3种方式的匹配率

图2是不同sigma值时3种情况的匹配率，由图可以看出，方式3比前2种方式的匹配率都高，匹配效果最好。在不同sigma值时，方式2有时比方式1的匹配率高，有时反而低，这是因为虽然经过拉普拉斯算子锐化后使得匹配点数增多，但是同时也会使得错误匹配点数增多，所以匹配率可能变大，也可能变小，这与sigma值有关，即与匹配图像本身质量有关;但是，如果匹配的时候利用双向匹配法，设定不同的阈值，这样可以删除很多错误匹配，从而使得匹配率增大，匹配效果较好。

3.2 实际图像实验

实验所用图像如图3所示，是标准测试图像中验证模糊不变性的图像[15]。图3中P1是清晰的图像，P2～P6为模糊的图像，模糊程度依次增大。实验的方法是分别用P2～P6与P1匹配。

图3 实验图像

将本文算法与直接由SIFT特征进行匹配的算法相比较，计算P2～P6与P1的匹配率，得到如图4所示的结果。可以看出P2～P6与P1匹配结果中，本文算法都比直接由SIFT特征进行匹配的算法要好，由于P2～P6图像模糊程度是逐渐增大的，直接利用SIFT特征进行匹配时的匹配率会逐渐减小，因为图像越模糊，检测的关键点越少。本文算法可以通过拉普拉斯算子锐化，将图像边缘增强，从而检测到的关键点数增加，再通过双向匹配法来减少错误匹配，进而达到很高的匹配率。例如，当图像很模糊时(图3中P6)，直接利用SIFT特征进行匹配的匹配率为96.91%，而本文算法的匹配率为99.02%。图5列出了2种方法对P1与P3的匹配结果。图5(a)是直接利用SIFT特征匹配的结果，图中显示明显有很多错误的匹配，而且总的匹配点数没有图5(b)中的总匹配点数多;图5(b)是本文算法的匹配结果，图中显示总的匹配点数较多，而且几乎没有错误匹配。总之，由实验结果可以看出本文的算法比基本的基于SIFT特征的匹配算法效果要好。

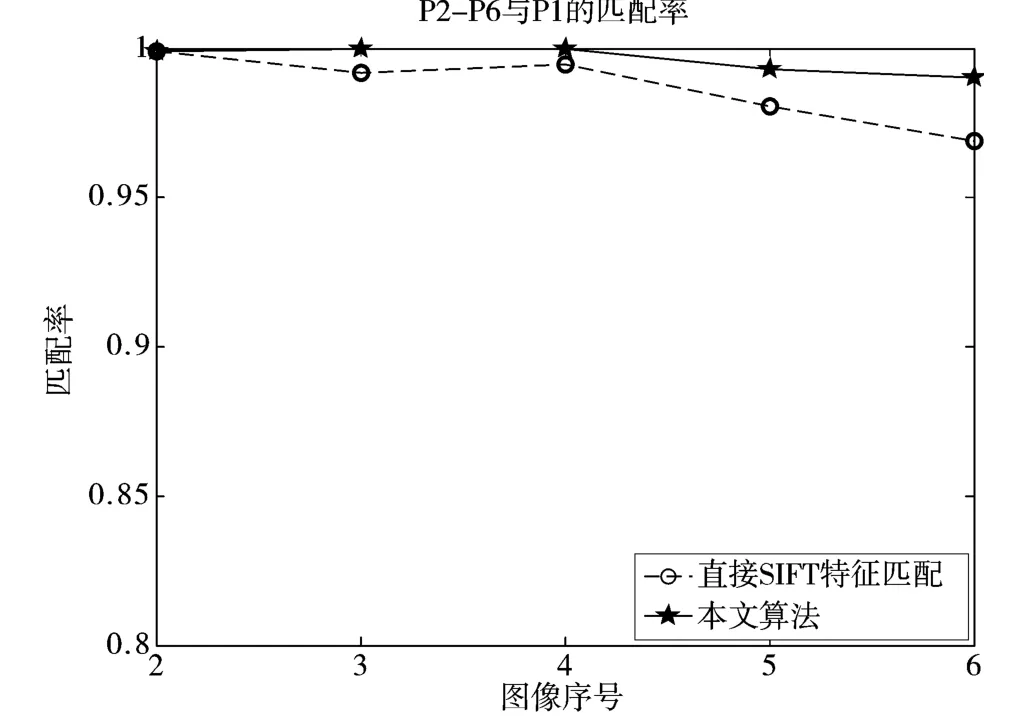
图4 匹配率

图5 P3与P1的匹配效果图

4 结束语

由于SIFT算法中要计算主方向，而主方向的计算是造成误差的一个主要原因[12]，但是本文在传统的SIFT算法的基础上，通过锐化处理和利用双向匹配算法进行特征匹配，从而减小了匹配误差，在没有改变SIFT算法本质的同时保证了匹配精度。实验结果表明本文提出的方法在提高匹配效果的同时可以加强基本SIFT算子进行匹配的模糊不变性。由于本文提出的方法增加了对图像的锐化处理，并进行双相匹配的操作，因此算法复杂度会增加。但是增加的时间复杂度相对原始算法本身的复杂度较小，所以在一定范围内可以利用本文所提出的算法进行匹配，以达到提高匹配率的目的。

[1] Lowe D G.Distinctive image features from scale-invariant keypoints[J].International Journal of Computer Vision，2004，60(2):91-110.

[2] Wu Jian，Cui Zhiming，Sheng V S，et al.A comparative study of SIFT and its variants[J].Measurement Science Review，2013，13(3):122-131.

[3] Ke Yan，Sukthankar R.PCA-SIFT:A more distinctive representation for local image descriptors[C]//Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition.2004，2:506-513.

[4] Bay H，Ess A，Tuytelaars T，et al.Speeded-up robust features(SURF)[J].Computer Vision and Image Understanding，2008，110(3):346-359.

[5] Mortensen E N，Deng Hongli，Shapiro L.A SIFT descriptor with global context[C]//Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition.2005，1:184-190.

[6] Abdel-Hakim A E，Farag A A.CSIFT:A SIFT descriptor with color invariant characteristics[C]//Proceedings of the 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition.2006，2:1978-1983.

[7] Morel J M，Yu Guoshen.ASIFT:A new framework for fully affine invariant image comparison[J].SIAM Journal on Imaging Sciences，2009，2(2):438-469.

[8] 高健，黄心汉，彭刚，等.一种简化的SIFT图像特征点提取算法[J].计算机应用研究，2008，25(7):2213-2215.

[9] 张官亮，邹焕新，秦先祥，等.基于改进SIFT特征和图转换匹配的图像匹配算法[J].计算机应用研究，2013，30(9):2861-2864.

[10] Heikkila M，Pietikainen M，Schmid C.Description of interest regions with local binary patterns[J].Pattern Recognition，2009，42(3):425-436.

[11] Gupta R，Patil H，Mittal A.Robust order-based methods for feature description[C]//Proceedings of the 2010 IEEE Conference on Computer Vision and Pattern Recognition.2010:334-341.

[12] Fan Bin，Wu Fuchao，Hu Zhanyi.Rotationally invariant descriptors using intensity order pooling[J].IEEE Transactions on Pattern Analysis and Machine Intelligence，2012，34(10):2031-2045.

[13] 骞森，朱剑英.基于改进的SIFT特征的图像双向匹配算法[J].机械科学与技术，2007，26(9):1179-1182.

[14] 阮秋琦.数字图像处理学[M].北京:电子工业出版社，2007.

[15] Katholieke Universiteit Leuven.Affine Covariant Features[DB/OL].http://www.robots.ox.ac.uk/～ vgg/research/affine/index.html，2007-07-15.