一种混合改进遗传算法的嵌套分区算法

2014-07-03宗德才王康康

计算机与现代化 2014年7期

宗德才，王康康，丁勇

(1.常熟理工学院计算机科学与工程学院，江苏常熟 215500;2.江苏科技大学数理学院，江苏镇江 212003;3.南京理工大学泰州科技学院计算机科学与技术系，江苏泰州 225300)

0 引言

旅行商问题(Traveling Salesman Problem，TSP)是一个典型的NP难的组合优化问题。该问题可描述为[1]:给定n个城市和两两城市之间的距离，要求确定一条经过各城市当且仅当一次的最短巡回路径。

假设有n个城市，用1～n对城市进行编号，1表示城市1，2表示城市2，…，n表示城市n。Θ是所有1，2，…，n 排列的集合，di，j是城市 i到城市 j的距离，s=(a1，a2，…，an)是 1，2，…，n 的一个排列，(a1，a2，…，an)表示访问的第1个城市是城市a1，第2个城市是城市a2，…，访问的最后一个城市是an，最后再回到第1个城市a1的一条回路。当di，j=dj，i时，称为对称 TSP 问题;当 di，j≠dj，i时，称为不对称TSP问题。本文中提到的TSP问题均是指对称TSP问题。

TSP问题可以用数学表达式表示为:

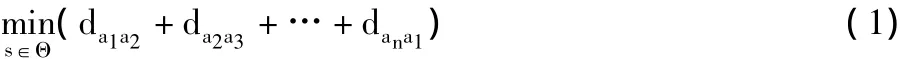
近年来，为解决TSP问题出现了许多随机优化算法或局部搜索算法，比较著名的有:遗传算法、粒子群算法、模拟退火算法、禁忌搜索算法、2-opt算法、3-opt算法、Lin-Kernighan(LK)算法等。这些算法能够在较短时间内获得近似解。嵌套分区算法(Nested Partitions Method，NPM)[2]是由 Shi Leyuan 等提出的一种能够高效求解大规模问题的优化方法，该算法提供了一个框架，能够将全局搜索与局部搜索相融合，具有易实现、并行性、全局性等优点。文献[3]将嵌套分区算法应用于银行分支机构选址问题，文献[4]将嵌套分区算法应用于大规模车间作业调度问题，文献[5]将嵌套分区算法应用于产品装配子序列合并问题，都取得了较好的效果。目前国内对于嵌套分区算法的研究还比较少。文献[6]将嵌套分区算法应用于求解旅行商问题，通过在抽样算子中引入2-opt局部搜索算法，对抽样得到的初始回路进行2-opt优化，能够显著提高解的质量和算法的收敛速度，但是能够搜索到最优解的概率不高，而且文献[6]中没有列出对具体的TSP问题实例的仿真结果。文献[7]将嵌套分区算法应用于置换流水作业优化调度问题，使用启发式算法对子域和裙域进行抽样，并对抽样点进行邻域搜索，该算法比单纯的启发式算法和邻域搜索算法有更好的寻优能力。文献[8]针对二次分配问题，在嵌套分区算法的基础上提出了一种禁忌嵌套分区算法，该算法结合了嵌套分区算法的全局搜索能力和禁忌搜索算法的局部搜索能力，获得了比嵌套分区算法和禁忌搜索算法更优的解。文献[9]提出了一种基于禁忌搜索的复合嵌套分区算法用于解决函数优化问题，在嵌套分区算法中加入禁忌搜索抽样算子后，减少了回溯次数，提高了嵌套分区算法的收敛能力。文献[10]提出了一种改进的嵌套分区算法，将其应用于节能ATP控制曲线的惰行点搜索，将禁忌搜索思想引入抽样算子，减少了回溯次数，增强了嵌套分区算法的局部搜索能力。

本文提出一种混合改进遗传算法的嵌套分区算法用于求解TSP问题，该算法用加权抽样法产生初始最可能域，用全局数组GL和GP保存每个区域的历史最优解，设计实现了一种子域交叉算子和子域变异算子，用改进的遗传算法搜索每个子域和裙域的最好解，在用改进遗传算法搜索裙域最好解的过程中，用改进的Lin-Kernighan算法优化种群中优秀的个体，对TSPLIB中问题实例的仿真实验结果表明，本文算法在求解旅行商问题时可以获得高质量的解。

1 嵌套分区算法求解TSP问题

定义1 回路。本文算法中用一个数组表示一条回路。例如，用一个数组 a=(1，6，2，9，8，4，5，7，3，10)表示从城市 1 出发，依次访问城市 6，2，9，8，4，5，7，3，10并且最后回到出发城市1的一条回路。

定义2 区域和区域长度。本文中用一个数组表示一个区域。用 regionk(region(1)，region(2)，…，region(k))，(1≤k≤n)(n表示城市个数)表示第1个城市固定为城市region(1)，第2个城市固定为城市region(2)，…，第k个城市固定为城市region(k)，剩下的n－k个城市的访问顺序未确定的区域，称k为此区域的长度。一个区域中可以包含一条或多条回路。

例如，对于10个城市的TSP问题，有2条回路a=(1，6，2，9，8，4，5，7，3，10)，b=(1，6，8，2，9，4，5，7，3，10)，则回路 a 不属于区域 region3(1，6，8)，回路b 属于区域 region3(1，6，8)。

定义3 单解域。对于TSP问题，只含有一条回路(一个单解)的区域称为单解域。

定义4 子域和父域。如果一个区域T是通过分割区域P得来的，则称T为P的子域，P为T的父域。

利用嵌套分区算法求解旅行商问题时的基本过程如下:

1)分区[6]:本文中采用的是均匀分区方法。假设有n个城市，用1～n对城市进行编号，则整个解空间为所有1，2，…，n的排列的集合。选择城市1固定为访问的第1个城市，分别将城市2，3，…，n固定为访问的第2个城市，由此将城市1固定为访问的第1个城市的解空间分为n－1个子域，用同样的方法选择访问的第3个城市，从而将每个子域n－2等分。按照这种方法，直到所有的子域都成为单解域。如图1所示。需要说明的是，分别将城市1，2，…，n固定为访问的第1个城市的解空间包含的解是相同的。

图1 嵌套分区算法求解TSP问题的分区树

对于n个城市的TSP问题，分区树的最大深度是n－1。

2)抽样:本文采用加权抽样法[2]获得一个区域的多条回路。

3)选区[6]:如果本次迭代中具有最优可能性指数的区域是当前最可能域的子域，则将该子域作为下次迭代的最可能域。

4)回溯[6]:如果本次迭代中裙域的可能性指数为所有区域中最优的，则需要进行回溯操作。本文算法中回溯到截至目前为止所找到的最优解的父域。

定义5 裙域[6]。设整个解区域为Θ，利用均匀分区方法分割区域σ(k)为Mσ(k)个子域，并将除区域σ(k)外的其他区域合并成一个区域Θσ(k)，区域Θσ(k)称为裙域。

定义6 区域的可能性指数[6]。对于TSP问题，将每个区域中抽样得到的多个初始回路中的最短回路长度作为该区域的可能性指数。

2 嵌套分区算法的改进

2.1 混合改进遗传算法的嵌套分区算法

在嵌套分区算法中，如果能够减少一次回溯，就可以少抽样2N(Mσ(k)+1)次(其中Mσ(k)为每次分区的子域个数，N为每个子域和裙域的抽样个数)[11]，从而缩短寻优时间，提高收敛速度。

图2 混合改进遗传算法的嵌套分区算法求解TSP问题

为了减少回溯的次数和加快收敛速度，本文用全局数组保存求解过程中获得的每个区域的历史最优解。使用全局数组GL记录每个区域的最短回路长度，即GL(1)记录区域region2(1，2)的最短回路长度，GL(2)记录区域region2(1，3)的最短回路长度，GL(3)记录区域region2(1，4)的最短回路长度，…，GL(n－1)记录区域region2(1，n)的最短回路长度。同理，用一个全局数组GP记录每一区域的最短回路。令GL(1)，…，GL(n－1)的初始值为80 000(一个较大值)，令m=0(m用来记录某个单解域的回路连续属于同一个最可能域的次数)，当m≥5，即连续5次某个单解域的回路长度最短，输出最优回路和长度。

混合改进遗传算法的嵌套分区算法求解TSP问题的流程图如图2所示。

使用加权抽样法产生初始最可能域的算法如下:

在中小规模TSP问题中，使用本文算法的回溯策略时，当p=0.99时可以获得质量最好的解[6]。因此，在本文算法中令p=0.99。

2.2 改进遗传算法搜索子域的最好解

根据城市之间的距离，计算距离每个城市由近到远的10个城市，生成k-近邻点集(k=10)。

设种群个数为m1，进化代数为gens，用加权抽样法产生子域regionk(region(1)，region(2)，…，region(k))的m1个初始个体，删除种群中相同的个体，只保留一个，用k-近邻法产生新的个体代替被删除的个体，得到初始种群 P1、P2、…、Pm1，计算出个体 P1、P2、…、Pm1的路径长度为 L1、L2、…、Lm1。

设每个个体的局部最优解为 PLb1、PLb2、…、PLbm1，其对应的长度为 PLl1、PLl2、…、PLlm1。

令 PLbi=Pi，PLli=Li，1≤i≤m1，计算出子域regionk(region(1)，region(2)，…，region(k))的全局最优个体PGB及其长度为PGL。

将个体Pj与子域regionk(region(1)，region(2)，…，region(k))的全局最优个体PGB使用子域交叉算子进行交叉操作，得到个体Pc1j;

将个体Pc1j与局部最优个体PLbj使用子域交叉算子进行交叉操作，得到个体Pc2j;

将个体Pc2j使用倒置变异和带约束的3-opt优化算子进行3-opt优化变异，得到Pm2j，计算出路径长度为 Lmj;如果 Lmj＜ Lj，或 Lmj＞ Lj并且(Lmj－ Lj)/Lj＜0.1，则 Pj=Pm2j;

如果 Lmj＜PLlj，则 PLbj=Pm2j，PLlj=Lmj;

End For

根据每个个体最新的局部最优解 PLb1、PLb2、…、PLbm，更新子域 regionk(region(1)，region(2)，…，region(k))的全局最优个体PGB及其长度PGL。

End For

输出子域regionk(region(1)，region(2)，…，region(k))的全局最优个体PGB作为子域regionk(region(1)，region(2)，…，region(k))的最好解。

2.2.1 子域交叉算子

对于子区域regionk(region(1)，region(2)，…，region(k))加权抽样法得到的初始解为 P1、P2、…、Pm1(m1为抽样个数)，选择2个个体 Pi和Pj进行交叉，设Pi表示为p(1)，p(2)，…，p(n)，Pj表示为 q(1)，q(2)，…，q(n)，其中 p(1)=q(1)=region(1)，p(2)=q(2)=region(2)，…，p(k)=q(k)=region(k)，Pi和Pj交叉操作后所得的子个体也属于子区域 regionk(region(1)，region(2)，…，region(k))的方法如下:

1)在父体Pj中随机选择一个参考城市q(r)，r≥k且 r≤n－1;

2)在父体Pi中找到城市p(u)=q(r)，p(v)=q(r+1)，如果 d(p(u)，p(v))+d(p(v)，p(u+1))+d(p(v－1)，p(v+1))＜d(p(u)，p(u+1))+d(p(v－1)，p(v))+d(p(v)，p(v+1))(d(x，y)表示城市x与城市y之间的距离)，即在父体Pi中删除城市p(v)，然后在城市p(u)与p(u+1)之间插入城市p(v)，得到新的个体Pi1;

3)依次在父体Pj中取参考城市q(r+1)，…，q(n－1)，重复步骤2)，直到最终生成子个体Pi1;

4)将父体Pi和父体Pj相互交换，重复步骤1)、2)和3)，得到子个体Pj1。

使用以上方法可以保证交叉操作产生的子个体Pi1和Pj1属于子区域 regionk(region(1)，region(2)，…，region(k))。

2.2.2 子域变异算子

1)倒置变异。

在一个个体中随机选择2个不同的城市，将这2个城市之间组成的路径逆序，得到变异后的个体。

对于子区域regionk(region(1)，region(2)，…，region(k))中的个体 Pi，设 Pi表示为 p(1)，p(2)，…，p(n)，其中 p(1)=region(1)，p(2)=region(2)，…，p(k)=region(k)，对个体Pi倒置变异后所得的个体Pmi也属于子区域regionk(region(1)，region(2)，…，region(k))的方法如下:

a)随机选择2个不同的城市p(i1)和p(i2)，i1≠i2且 k≤i1，i2≤n。

b)将城市p(i1)和p(i2)之间组成的路径逆序，得到 Pmi。

2)带约束的3-opt优化算子。

3-opt算法[12]是局部搜索算法中效率最高的kopt邻域算法，其基本过程是:设T是一条初始回路，产生3个随机位置t1、t3、t5，它们的下一个节点分别记为 t2、t4、t6，对应的 3 条边的集合记为{(t1，t2)，(t3，t4)，(t5，t6)}，该算法断开这3条边试图找到另一个边的集合{a，b，c}，使得新产生的回路长度变小。这里是3条边则称为3-opt，如图3(a)所示。如果是2条边则称为2-opt，如图3(b)所示。对于k-opt(k≥2)，最后一个节点必须与第一个节点重合。

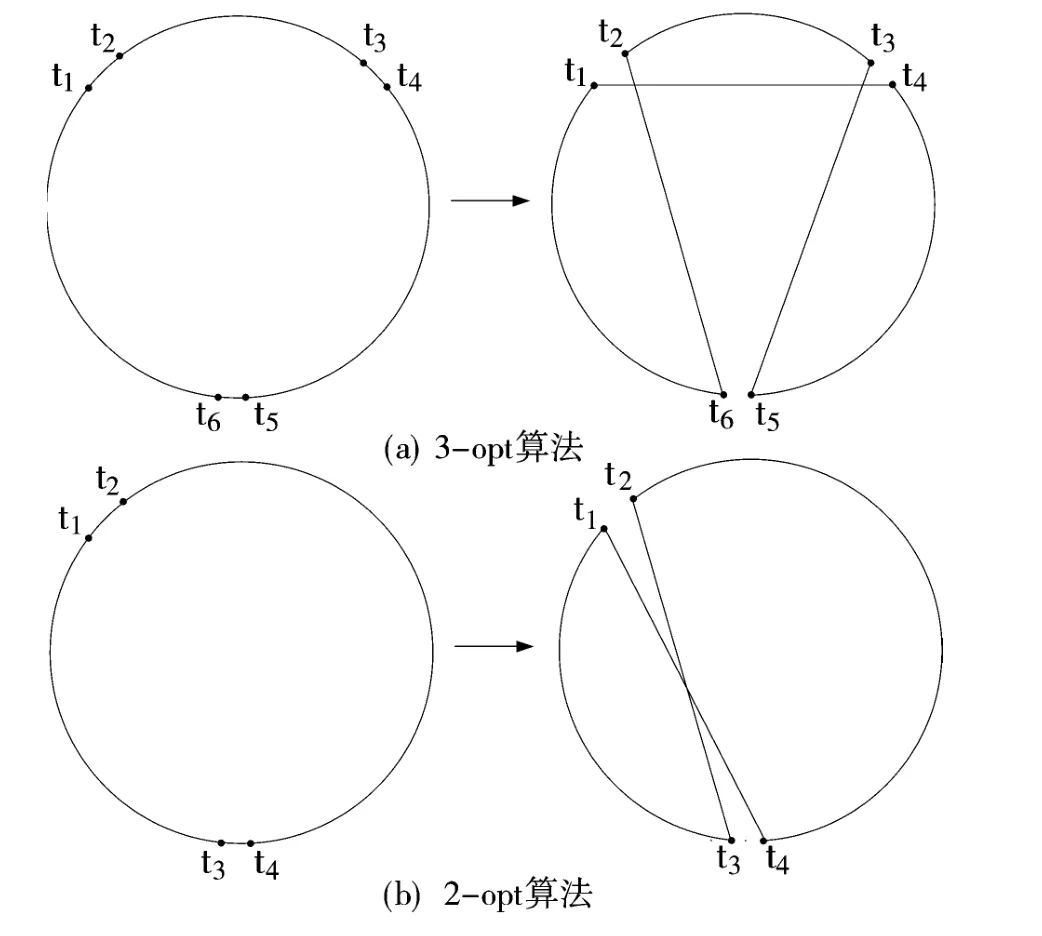
图3 3-opt算法和2-opt算法

对于一条巡回路径，3-opt局部搜索算法就是从巡回路径中选择两两互不相邻的3条边，将这条巡回路径分成3段路径，然后重组这3段路径，重组后有7条可能的巡回路径，如果这7条巡回路径中长度最短的巡回路径小于原来的巡回路径，则用此长度最短的巡回路径代替原来的巡回路径。

分析3-opt算法中边的移动过程，可以发现t1和t6一直是连在一起的，也就是说t1和t6之间的点的相对位置保持不变。利用3-opt交换的这一特性，文献[12]提出了一种带约束的3-opt优化方法，该方法能够保证对子区域regionk(region(1)，region(2)，…，region(k))中的个体Pi进行3-opt优化变异后所得的解也属于该子区域。

本文采用文献[12]中的方法对子区域regionk(region(1)，region(2)，…，region(k))中的个体Pi进行3-opt优化变异。

2.3 对Lin-Kernighan算法的改进

Lin-Kernighan算法[13]是 1971 年由 Lin Shen和B.W.Kernighan提出的一种解决对称TSP问题的有效的启发式方法。

Lin-Kernighan算法中只允许连续的边交换。实验结果表明[14]，不允许非连续的边交换会大大降低找到最优解的概率。为了提高找到最优解的概率，本文算法在发现连续的边交换不能再进一步改进解的质量时，便尝试进行非连续的边交换。非连续的边交换的具体执行过程如下。

1)如果2-opt交换产生了2个环路并且路径长度是减少的，则转到步骤1.1)，否则，转到步骤2)。

1.1)如果通过2-opt交换连接2个子环能够产生一条有效的回路，并且路径长度是减少的，则进行2-opt交换，如图4(a)所示，然后转步骤5)。

1.2)如果2-opt交换不能够减少路径长度，则尝试3-opt交换，如果通过3-opt交换连接2个子环能够产生一条有效的回路，并且路径长度是减少的，则进行3-opt交换，如图4(b)所示，然后转步骤5)。

1.3)如果3-opt交换不能够减少路径长度，则尝试4-opt交换，如果通过4-opt交换连接2个子环能够产生一条有效的回路，并且路径长度是减少的，则进行4-opt交换，如图4(c)所示，然后转步骤5)。

1.4)如果4-opt交换不能够减少路径长度，则尝试另一个4-opt边交换(换另一个t7)转步骤1.3);如果所有的4-opt交换都不能够减少路径长度，则回到步骤1.2)，尝试另一个3-opt边交换(换另一个t5)。

1.5)如果所有的3-opt都不能减少路径长度，则回到步骤1.1)，尝试另一个2-opt边交换(2-opt的变化情况较多:换另一个t4，换另一个t3，换另一个t1)。

1.6)如果所有的 2-opt交换、3-opt交换、4-opt交换都不能减少路径长度，则转步骤2)。

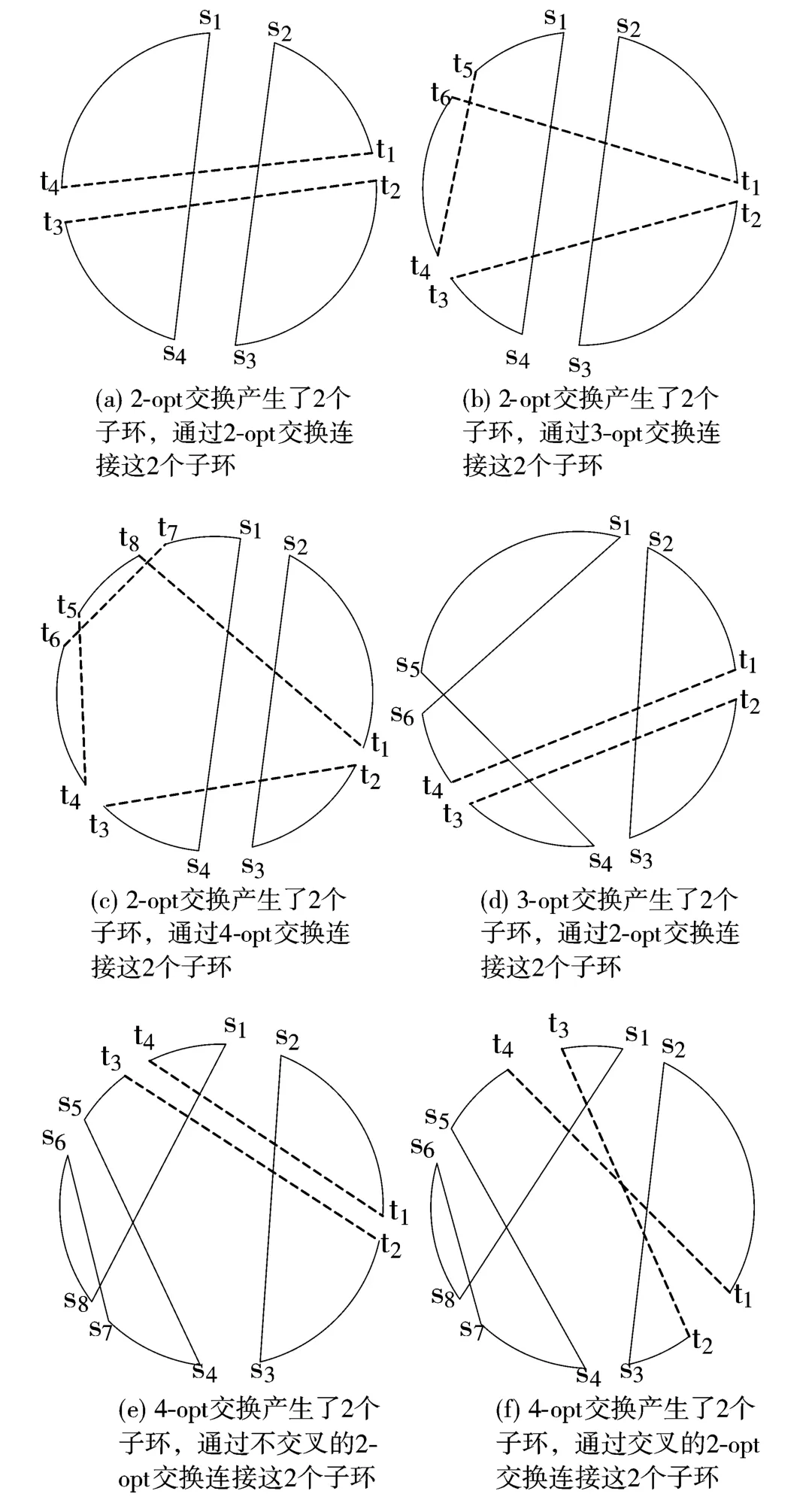
图4 非连续的边交换

2)如果3-opt交换产生了2个环路并且路径长度是减少的，则转到步骤2.1)，否则，转到步骤3)。

2.1)如果通过2-opt交换连接2个子环能够产生一条有效的回路，并且路径长度是减少的，则进行2-opt交换，如图4(d)所示，然后转步骤5)。

2.2)如果通过2-opt交换连接2个子环能够产生一条有效的回路并且路径长度是增加的，则尝试另一个2-opt边交换(2-opt的变化情况较多:换另一个t4，换另一个t3，换另一个t1)，然后转步骤2.1)。

2.3)如果所有的2-opt交换都不能减少路径长度，则转步骤3)。

3)如果4-opt交换产生了2个环路并且路径长度是减少的，则转到步骤3.1)，否则，转到步骤4)。

3.1)如果通过2-opt交换连接2个子环能够产生一条有效的回路，并且路径长度是减少的，则进行2-opt交换，如图4(e)或4(f)所示，然后转步骤5)。

3.2)如果通过2-opt交换连接2个子环能够产生一条有效的回路并且路径长度是增加的，则尝试另一个2-opt边交换(2-opt的变化情况较多:换另一个t4，换另一个t3，换另一个t1)，然后转步骤3.1)。

3.3)如果所有的2-opt交换都不能减少路径长度，则转步骤4)。

4)尝试另一个4-opt边交换，转步骤3);如果所有的4-opt边交换都尝试过了，则尝试另一个3-opt边交换，转步骤2);如果所有的3-opt边交换都尝试过了，则尝试另一个2-opt边交换，转步骤1)。

5)结束非连续的边交换，返回改进解。

2.4 改进遗传算法搜索裙域的最好解

用改进遗传算法在搜索裙域最好解的过程中，设种群个数为m2，产生初始种群时，从全局数组GP中选择qr个个体作为裙域的初始种群的一部分个体，其他m2-qr个个体用k-近邻法产生，设进化代数为genq。

用改进遗传算法搜索子域的最好解时，存在很多限制条件，交叉操作和变异操作都必须保证产生的解仍然属于该子域。而在用改进遗传算法搜索裙域的最好解时，交叉操作时需要将子域交叉算子中r≥k这个条件去掉，变异操作时不必使用带约束的3-opt优化算子，而只需使用一般的3-opt优化算法，并且可以将倒置变异中k≤i1，i2≤n这个条件去掉。在每一代进化结束后，选择每一代种群中互不相同的最优秀的5个个体，用改进的Lin-Kernighan算法进行优化，然后保存这一代中属于该裙域的最好解，在genq代进化结束后，输出所有代中属于该裙域的最好解作为该裙域的最好解。

3 实验结果与分析

本文算法运行环境如下:CPU为Intel Pentium 4 2.40 GHz;内存为 1 GB;操作系统为 Windows XP sp3;开发工具及开发语言分别为 DEV-CPP-4.9.9.2、C语言。为了测试算法的性能，对每一个TSP问题，都运行30次。

对于Berlin52问题、Eil51问题和st70问题，m1取20，gens取 30，m2取 30，qr取 20，genq取 50;对于Eil76问题、rd100问题、Eil101问题、Lin105问题、pr107问题、pr124问题、Ch130问题、Ch150问题、pr152问题、rat195问题、kroA200问题，m1取20，gens取40，m2取 50，qr取 30，genq取 80;对于 A280 问题、pcb442 问题，m1取20，gens取 50，m2取60，qr取30，genq取100。将加权抽样法产生初始最可能域时的参数d设为10。

表1的仿真结果表明，本文算法对于200个以内城市的TSP问题能够在40秒以内求得TSP问题的最优解。但是对于200个以上城市的TSP问题，随着城市规模的扩大，求得最优解的时间稍长。

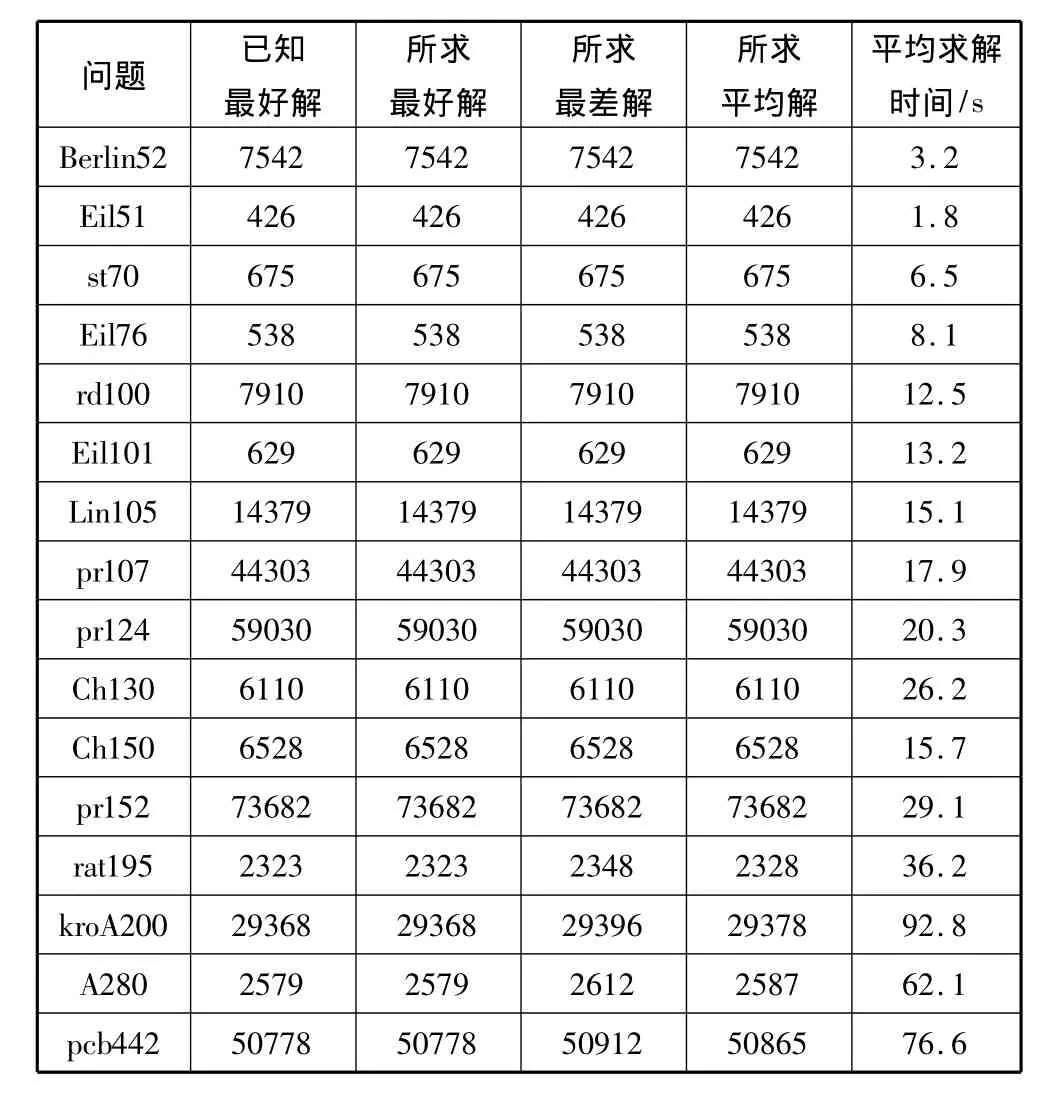
表1 本文算法对TSPLIB中部分问题的仿真结果

为了比较本文算法和文献[12]中算法的平均求解时间，将文献[12]算法在本文算法的运行环境中重新运行，对文献[12]中的每一个TSP问题都运行30次，然后计算平均求解时间。

文献[15]算法的硬件环境为Pentium Dual-Core CPU 2.20 GHz，内存2.0 GB，编程语言为 C++，显然文献[15]算法的硬件环境优于本文算法而编程语言与本文相似。

文献[12]提出了一种改进的嵌套分区算法，用3-opt算法改进每个区域解的质量，对于100个城市以下的TSP问题求解质量较高。表2将本文算法与文献[12]中算法的平均求解时间进行了比较，本文算法平均能够在13 s之内求得100个以下城市的最优解，而文献[12]中算法的平均求解时间明显较长，特别是对于rd100问题，本文算法平均能够在12.5 s内求得最优解，而文献[12]中算法平均需要105.2 s才能求得最优解。

文献[15]提出了一种基于距离的改进量子交叉遗传算法，通过在选择城市时加入父代优质解的信息，提高了交叉所产生新解的质量，从而提高了算法的寻优能力。表2将本文算法与文献[15]中算法的平均求解时间进行了比较，结果表明虽然本文算法的硬件配置要低于文献[15]中的，但是对于每一个TSP问题，本文算法都能更快地求得最优解，对于200个以上城市的TSP问题，随着城市规模的增加，本文算法与文献[15]中算法的平均求解时间差距逐渐加大。

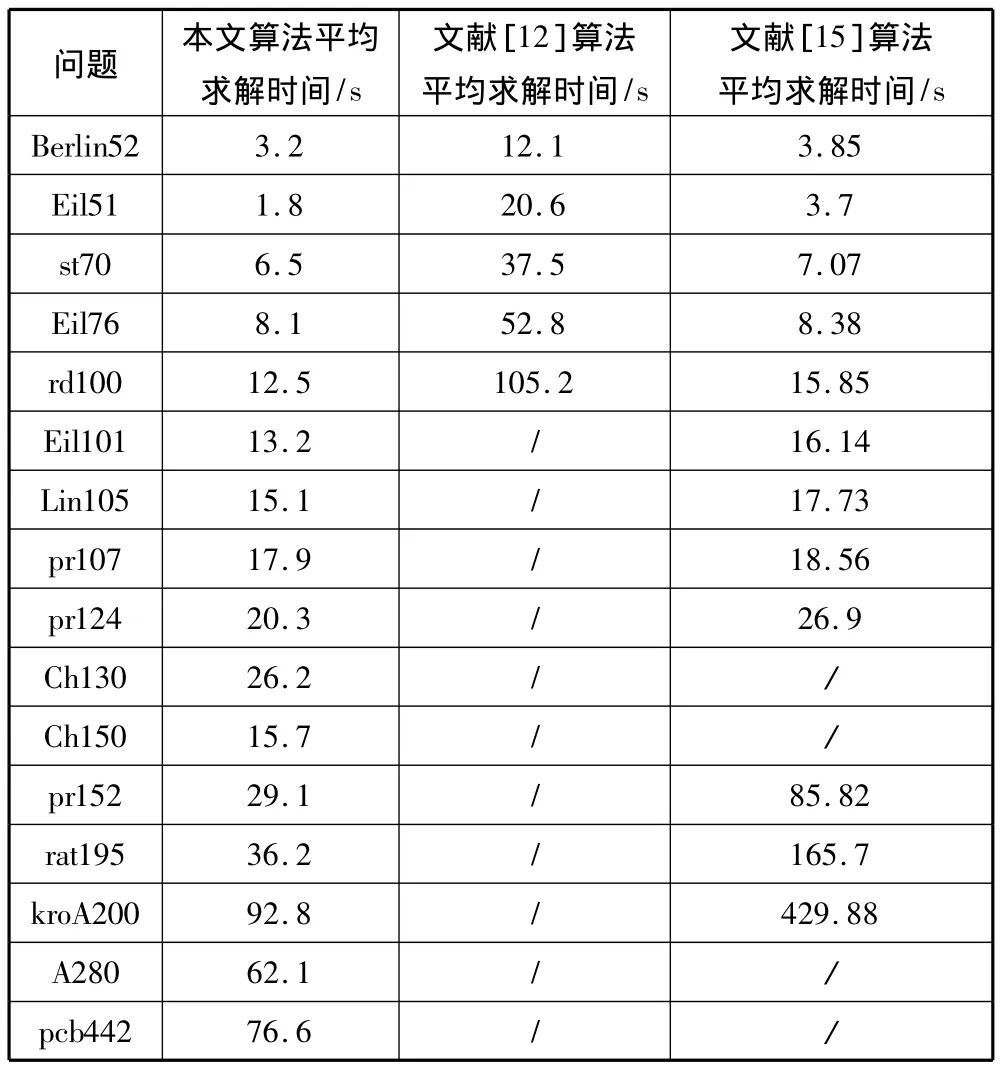
表2 参考文献中的平均求解时间比较

表2中“/”表示文献中没有对相应的TSP问题进行仿真，没有仿真结果。

表3将本文结果与文献[12，15-18]的部分结果进行了比较，结果表明本文算法能够找到所有问题的最好解，求得的最短路径长度最短，求解质量最高。文献[12]对于100个以下城市的TSP问题都找到了最优解，但是求解时间较长;文献[15]的算法对于表3中的12个TSP问题都没有找到最优解，求解质量最差。

文献[16]提出了一种改进的蚁群算法，该算法采用信息素挥发因子自适应调整机制，同时根据公共路径降低蚁群算法运算时间并提高了算法的搜索能力。对于Eil51问题，将改进算法连续运行15次，找到的最短路径长度为427，没能找到最优解426。

文献[17]提出了一种模糊人工蜂群算法，将模糊输入输出机制引入到算法中实现蜜源访问概率的有效调整，避免算法陷入局部极值。文献[17]的算法对于Eil76问题和Ch150问题没有找到最优解。

文献[18]将大洪水算法与2-opt算法融合在一起，提出了求解TSP问题的改进大洪水算法。文献[18]的算法对于Eil101问题、Ch130问题和rat195问题没有找到最优解。

表3 参考文献中的求解质量比较

表3中“/”表示文献中没有对相应的TSP问题进行仿真，没有仿真结果。

表3中求的是最短路径长度，数值越小，解的质量越高。

4 结束语

本文在原有算法基础上，提出了一种混合改进遗传算法的嵌套分区算法。该算法用加权抽样法产生初始最可能域，设计实现了一种子域交叉算子和子域变异算子，并提出了一种改进的遗传算法，然后，用改进的遗传算法搜索每个子域和裙域的最好解。在用改进遗传算法搜索裙域最好解的过程中，改进了Lin-Kernighan算法，用改进的Lin-Kernighan算法优化种群中优秀的个体。对TSPLIB中16个问题实例的仿真实验结果表明，本文算法在求解旅行商问题时可以获得高质量的解。但是对于城市规模较大的问题求解时间稍长。下一步将对交叉算子和Lin-Kernighan算法进行进一步改进，使之能解决更大规模的TSP问题。

[1] 张家善，王志宏，陈应显，等.一种求解旅行商问题的改进遗传算法[J].计算机系统应用，2012，21(9):192-194.

[2] Shi Leyuan，Olafsson S.An integrated framework for deterministic and stochastic optimization[C]//Proceedings of the 1997 Winter Simulation Conference.1997:358-365.

[3] Xia Li，Yin Wenjun，Dong Jin，et al.A hybrid nested partitions algorithm for banking facility location problems[J].IEEE Transactions on Automation Science and Engineering，2010，7(3):654-658.

[4] Yau Hoksung，Shi Leyuan.Nested partitions for the largescale extended job shop scheduling problem[J].Annals of Operations Research，2009，168(1):23-39.

[5] Zhou Wei，Zheng Jianrong，Wang Junfeng.Nested partitions method for assembly sequences merging[J].Expert Systems with Applications，2011，38(8):9918-9923.

[6] 刘昌军，苏琴，卫军胡，等.嵌套分割算法在旅行商问题上的应用[J].系统仿真学报，2008，20(24):6858-6861.

[7] 武维，管晓宏，卫军胡.Flow shop问题的嵌套分区优化调度方法[J].控制理论与应用，2009，26(3):233-237.

[8] 武维，卫军胡，管晓宏.一种求解QAP问题的混合嵌套分区优化算法[J].控制与决策，2010，25(6):889-893.

[9] 宋建强，马良.基于禁忌搜索的复合嵌套分割算法[J].计算机应用研究，2011，28(4):1260-1262.

[10] 刘晓娟，邓子渊.改进的嵌套分割算法及其在节能惰行中的应用[J].计算机工程与应用，2013，49(10):239-242.

[11] 路晓伟，蒋馥.基于模拟退火的复合嵌套分割算法[J].系统工程与电子技术，2004，26(1):99-102.

[12] 宗德才，王康康.改进的嵌套分区算法求解旅行商问题[J].计算机工程与应用，2011，47(24):54-57.

[13] Lin Shen，Kernighan B W.An effective heuristic algorithm for the traveling salesman problem[J].Operations Research，1973，21(2):498-516.

[14] 田伟，田国会，张攀，等.考虑非对称情形的一类拣选问题的改进 LK算法求解[J].中国工程科学，2004，6(11):47-52.

[15] 杨玉，李慧，戴红伟.改进量子交叉遗传算法在TSP问题中的应用[J].南京师范大学学报(工程技术版)，2012，12(3):43-48.

[16] 申铉京，刘阳阳，黄永平，等.求解TSP问题的快速蚁群算法[J].吉林大学学报(工学版)，2013，43(1):147-151.

[17] 柳寅，马良.模糊人工蜂群算法的旅行商问题求解[J].计算机应用研究，2013，30(9):2694-2696.