利用Matlab模拟点电荷系的电场线和等势面

陈 伟，易志俊，丁益民

(湖北大学，湖北 武汉 430062)

电场线和等势面是描述电场性质的重要的物理量，在物理教学中，通常需要绘制点电荷系的电场线和等势面，因此研究用计算机绘制电场线和等势面具有重要的现实意义。Matlab是一种广泛应用于科研、工程计算和数值分析的高级语言，它以矩阵为基本的数据操作对象，进行高性能的数值计算和符号计算，并拥有强大的绘图功能。在物理仿真中具有明显的优势。

近年来许多老师对用Matlab模拟点电荷电场进行了研究。莫照等人通过数学建模的过程，将物理问题变成了数学问题，进而用Matlab模拟了双“点电荷”的电场和等位线［1］;王明美也通过Matlab模拟了两个点电荷体系的电场线和等势线［2-3］;向罗杰等人结合电场方程和泰勒展开式，分析电场线的性质，利用Mathematica模拟了共线的三个点电荷电场线的分布［4］。

本文首先计算出点电荷系在平面某点的电势叠加，利用Matlab的命令绘出等势面，然后结合电场线和等势面的垂直关系，绘出电场线。这里对点电荷的分布以及电荷量没有特殊要求，由用户自己根据实际需要在一定范围内输入点电荷系的位置和电荷量，即可显示出其电场线和等势面，具有良好的普遍性和交互性，便于学生对点电荷系电场的规律进行探究式的学习。

1 基本原理

若平面真空中存在若干点电荷，记为Q1、Q2、Q3……Qn，根据电势的叠加原理，可得这个点电荷系所激发的电场中某点p的电势为

式中:ri为点电荷Qi到 p点的距离［5］。

建立平面直角坐标系，设p点坐标为(x，y)，Qi所在位置的坐标为(xi，yi)，对于某一确定的p点，可令Up=c，c为某一定值，那么(1)式可改写为

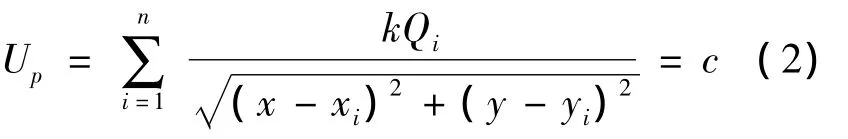
实际上，满足(2)式的p点不止一个，因此方程是点电荷系产生电场中电势恒为c的一个等势面方程［6］。如果c取不同的值，可以得出不同的等势面。根据等势面的画法要求，一般按等差数列的变化对c取值，并由(2)式得到一系列的等势面方程［7］。

结合等势面方程，用Matlab编写程序绘出等势面，再根据电场线垂直于等势面，对电势求梯度，即可描绘出电场线。

2 程序设计

以三个点电荷为例，电荷量分别为 Q1、Q2、Q3，对应坐标为(x1，y1)、(x2，y2)、(x3，y3)，于是，由(2)式得到某一点p(x，y)的电势为

主要思路如下:

(1)按提示依次输入三个点电荷的位置及电荷量，以电荷1为例:

disp('对电荷1');

rc1=input('输入电荷1位置［x，y］');

x1=rc1(1);

y1=rc1(2);

q1=input('输入电荷量(库伦):');

(2)利用(3)式计算出这三个点电荷在某点p(x，y)的电势叠加，并运用Matlab的绘图命令contour绘出若干个等势面［7］。主要代码如下:

%计算出三个电荷在p点的合电势

%设置电势的等差数列

%绘制等势面

(3)绘制电场线，首先找个起点，计算出该点的坐标，然后根据电场线和等势面的垂直关系，利用命令 streamline绘出电场线［8］。主要代码如下:

%对电势求梯度

%设置第一个点电荷电场线角度间隔

%电场线的角度范围

r0=0．1;%电场线起点半径

x1=r0*cos(th1)+x1;%电场线起点横坐标

y1=r0*sin(th1)+y1;%电场线起点纵坐标

streamline(X，Y，Ex，Ey，x1，y1);%画电场线

该设计思路简洁，逻辑清晰。用户还可以改变电荷的位置和电荷量，从而对电场线和等势面进行对比和分析。

3 模拟结果及分析

3．1 三个等量、同号点电荷等势面及电场线的模拟

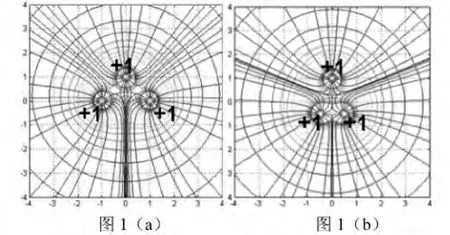
图1 同号、等量点电荷的等势面及电场线

从图1中可以看出电场线不相交，开始时三个点电荷下面的电场线和等势面比较密集，但由于下面两个电荷的靠近以及与上面电荷的远离，下面变的稀疏，而上面的变得密集了。

3．2 三个同号、不等量点电荷等势面及电场线的模拟

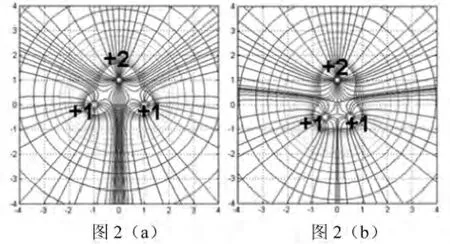
图2 同号、不等量点电荷的等势面及电场线

由于上面点电荷电荷量的增加，其周围的电场线变的密集。

3．3 三个等量、异号点电荷的等势面及电场线的模拟

图3 等量、异号点电荷的等势面及电场线

从图3中看到，电场线从正电荷出发，到负电荷终止，而且由于电荷位置的调整，上面负电荷的电场线重新分布，变得下密上疏。

3．4 三个不等量、异号点电荷的等势面及电场线的模拟

图4 不等量、异号点电荷的等势面及电场线

由于上面的点电荷电量增加，其电场线变多，而且靠近正负电荷中间位置的电场线密集，而远离中间位置的稀疏。

总之，从以上四种情况的图中我们可以知道，电场线和等势面是通过模拟来反应电荷性质的，电荷量大的电荷周围的电场线和等势线密集，而电荷量小的电荷周围的稀疏;同种点电荷之间的电场线和等势线稀疏，而异种点电荷之间的密集;同种点电荷距离较近时电场线和等势线稀疏，而异种点电荷距离较近时电场线和等势线密集［9］。这些与实际情况相符，所以模拟效果明显。

4 结 论

本文用Matlab模拟了三个点电荷电场线和等势面，并通过改变它们的位置及电荷量，分析比较了不同情况下的分布情况，具有简单和清晰的特点，并且具有较好的普适性和交互性。该模拟程序不仅能在物理实验的教学中起到很好的演示作用，通过调整输入的参量，还可观察多种情况下点电荷系的电场线与等势面，便于学生进行探究式学习。同时它还可使教学过程更生动和形象，激发学生的学习热情。

［1］ 莫照，胡奇光．用MATLAB模拟双“点电荷”的电场和等位线［J］．电脑学习，2007(2)．

［2］ 王明美．一对点电荷电场的 MATLAB模拟实验［J］．合肥师范学院学报，2012(3)．

［3］ 刘雅彬，鲁晓东．MATLAB对静电场等势线的最小二乘描绘［J］．大学物理实验，2013，2(26):82-84．

［4］ 向罗杰，王慧，赵钊．平面点电荷体系的电场线模拟［J］．实验科学与技术，2010(6)．

［5］ 丁益民，徐扬子．大学物理实验［M］．北京:科学出版社．2008．

［6］ 张毅，丁益民．基于Visua C++的非线性电路实验模拟［J］．大学物理实验，2010(3)．

［7］ 王静，王亚芳，董爱国，等．利用Matlab模拟静电场的分布［J］．科技创新导报，2012(17)．

［8］ 陈宗文，魏秀芳，雒向东．用MATLAB解决电磁学中的静电场问题［J］．无线互联科技，2012(12)．

［9］ 周江，黄刚，莫济成，等．长直平行带电体静电场的MATLAB 模拟［J］．科技信息，2009(7)．

［10］江略，丁益民．基于OpenGL的三维电场线模拟［J］．大学物理实验，2011(5)．