作图法研究物理实验数据处理中的线性回归问题

方晓懿，薛滨杰

(成都理工大学，四川成都 610059)

最小二乘法拟合直线是物理实验中的常用数据处理方法，一般用计算机数据处理软件准确求出直线回归方程系数、相关系数、标准差以及不确定度等。教学中也常用用作图法画出直线并求出直线方程系数，优点是直观方便，但现行教材中大多没有给出其标准差和相关系数的计算方法。本文以铜-康铜热电偶的温差电动势E测量为例，根据最小二乘法原理作回归直线，根据标准差的概念作标准差平行四边形，计算直线回归方程标准差和相关系数［1-2］。

1 用最小二乘法进行线性回归

假定变量x和y的关系是线性的，且y方向的误差远大于x方向的误差，对测得的一组数据xi，yi(i=1，2，…，k)，用最小二乘法进行线性回归，可得直线的回归方程［3］

斜率为

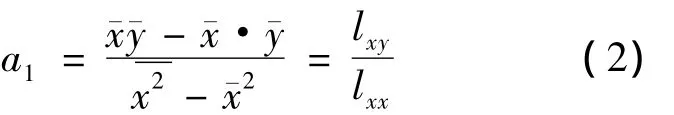
截距为

其中，

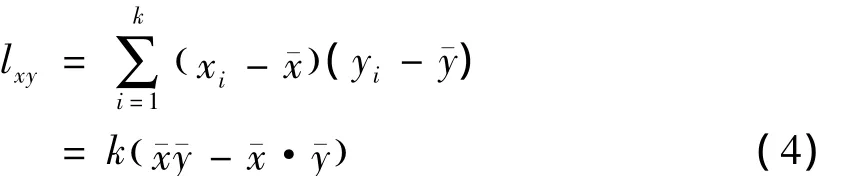
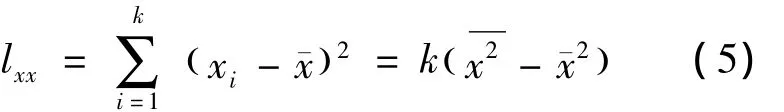
同样，令

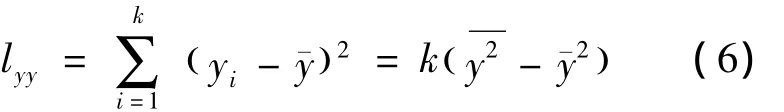
定义相关系数为

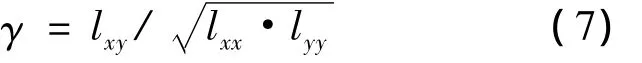
yi的剩余标准误差差s为

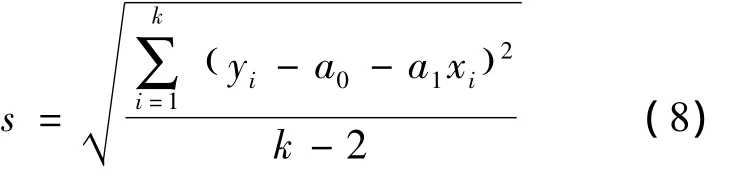
斜率a1和截距a0的标准差分别为为

或

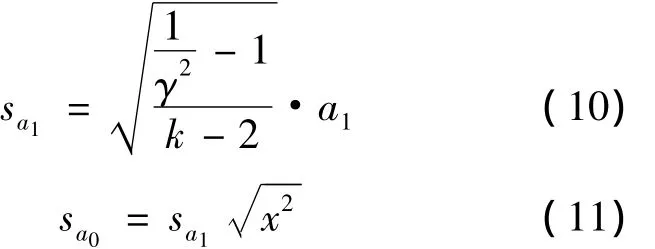
用Excel中的回归方法可计算出回归方程、相关系数、标准差及不确定度［4-5］。

2 用作图法研究一元线性回归方程

2．1 作回归直线和标准差差平行四边形

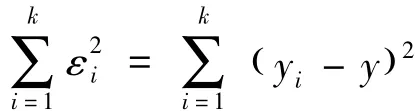
如图所示，在xoy平面上根据(xi，yi)描点，作直线a0b．根据最小二乘法，作出的直线a0b应使为最小．其中yi和y分别为x=xi时的数据点和回归直线a0b在y方向的值．显然εi=yi－y等于数据点在y方向上离开a0b的距离．要使为最小，就要使以εi为边长的正方形面积之和为最小．这样，作a0b时，应使数据点尽可能地靠近a0b，并且在a0b两侧的数据点数量大致相等，见图1。

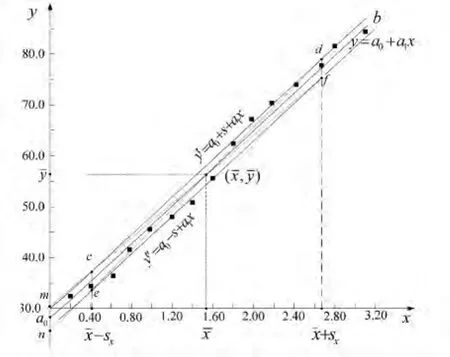
图1 回归直线和标准差平行四边形图

作两条与a0b平行且等距的直线，使它们包含的数据点，剩余的点比较均匀地分布在两条平行线外．这两条平行线的方程为

这样，在出现的(xi，yi)全部数据中，约有67% 的点落在这两条直线之间的范围内［1］．

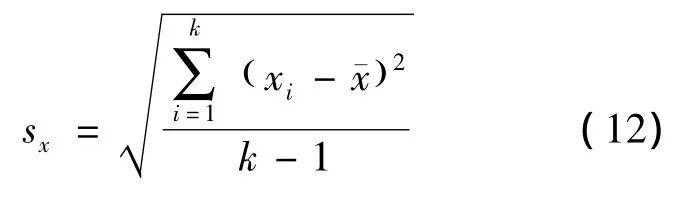
作cdef的对角线cf和ed，并延长，使之与y轴相交于m和n点．cf、de和a0b三条线的交点为平均值点。

2．2 求 sa1和 sa0

由式(5)、(9)和(12)有

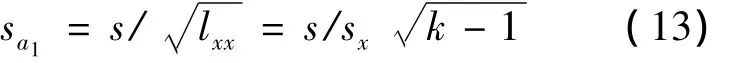
将式(12)代入式(5)可得

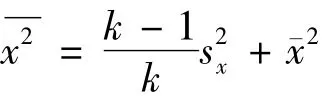
这样式(11)变为

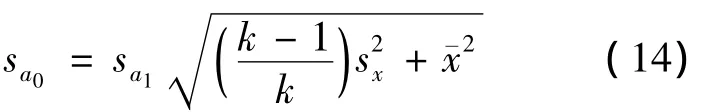
令，式(14)可写成

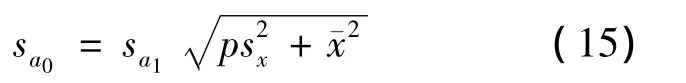
当测量次数k较大时，近似地有

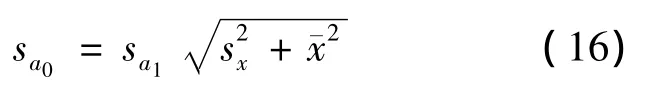
从图1中求出s、sx和x¯便可计算sa1和sa0。

2．3 求相关系数γ

由(10)式得

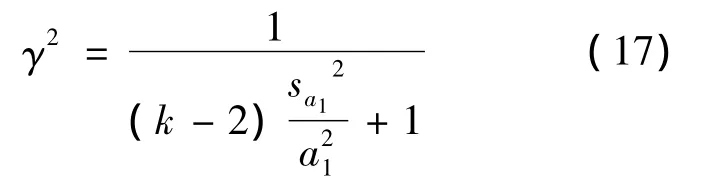
将(13)式代入，得

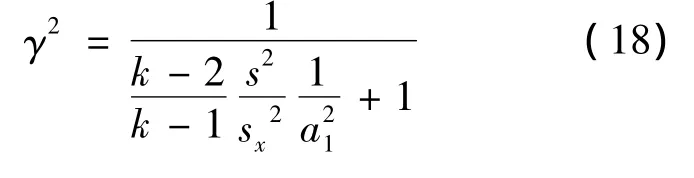
令k－2=g，式(18)可写成

k－1

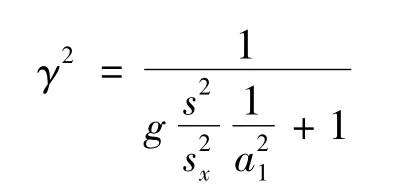
由1图可知，cf和ed的斜率分别为

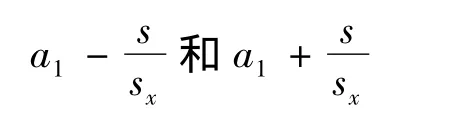
由此求出

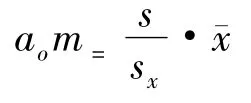
这样有

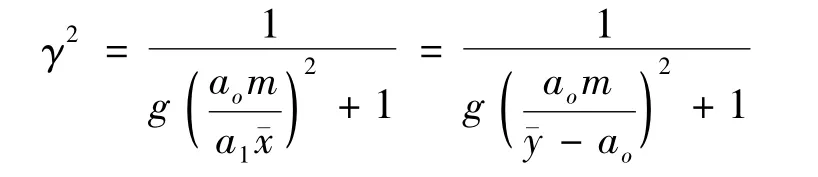
再从图1中可知

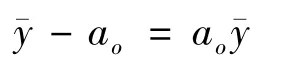
当测量次数k较大时，近似地有

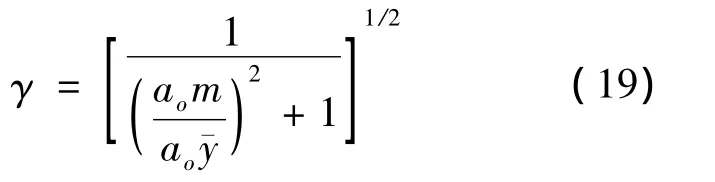
3 举 例

测得某铜-康铜热电偶的温差电动势E与温度t的对应数据如表1所示。

表1 某铜-康铜热电偶的温差电动势E与温度t的对应关系

按表1数据作回归直线，并作偏差平行四边形及对角线，如图1所示。

从图中可得

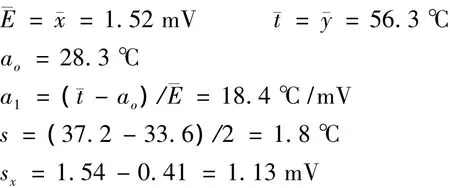
表2是用Excel中的回归方法和作图法求这例线性回归方程的数据比较。

表2 计算法和作图法线性回归方程的数据比较

作图法与Excel的数据一致，作图法的误差主要是作图时代入的，它因人不同而不同．作图法中，回归方程的系数a0和a1、相关系数γ和剩余标准误差差s的误差不大，系数标准差sa0和sa1的误差较大，可能与作图及误差传递有关。

4 结 论

作图法求解一元线性回归方程概念清楚，图像直观，教学中有助于训练作图法处理物理实验数据，更重要的是加深对线性回归方程中最小二乘法、相关系数和标准差的理解。

［1］ 吕斯骅，段家怟．新编基础物理实验［M］．北京:高等教育出版社，2006．

［2］ 冯学超．Origin对物理实验数据处理重要性的分析［J］．大学物理实验，2013，26(1)．

［3］ 沈元华，陆申龙．基础物理实验［M］．北京:高等教育出版社，2003．

［4］ 蒋逢春，冯学超．示波器测电容方法对比分析及数据处理［J］．大学物理实验，2013，23(2)．

［5］ 姚列明．结构化大学物理实验［M］．北京:高等教育出版社，2009．