白光频谱干涉原理及其应用
2014-07-03杨永佳周自刚
杨永佳,周自刚,邱 荣,蒋 勇,闫 汇
(西南科技大学,四川绵阳 621010)
光的干涉是最基本的物理实验之一。在大学物理理论以及实验教学中曾经多次提到光发生干涉的基本条件为:两束光的频率相同、振动方向相同(或者说在某一方向的振动分量不为零)、位相差稳定[1]。当两束光的光程差小于相干长度时,可以观察到干涉现象。对于一台普通的激光器,其相干长度可以达到数十米乃至上千米,而钨灯等白光光源的相干长度却只有几微米,因此只有当从此类光源分出的两束光的光程差小于其相干长度时,才可以观察到干涉现象,此即通常所说的白光干涉,但是实验上实现存在一定的难度[2-4]。
事实上,上面提到的干涉均为时域的干涉,当从钨灯发出的两束光其光程差远远大于其相关长度时,在频谱域仍然能观察到干涉现象,即白光频谱干涉。由于白光频谱干涉与时域干涉存在本质上的不同,并且在微位移[5]、距离[6]、折射率[7-8]测量等方面有极高的灵敏度,因此近年来白光频谱干涉在上述领域已经得到了广泛应用。本文将详细讨论白光频谱干涉的基本原理及其在微位移测量中的应用,并将其与大学物理中的迈克尔逊干涉微位移测量实验进行对比,探讨了白光频谱干涉在大学物理理论与实验教学中的重要应用前景。
1 白光频谱干涉的基本原理
典型的白光频谱干涉光路见图1,从钨灯(Lamp)发出的白光首先经过一个针孔(Pin hole),针孔的位置在透镜(Lens)的前焦点上,因此从透镜出来的光为平行光,平行光经宽带分束镜(Beam splitter)分为两束,经反射镜 M1、M2反射后沿原路返回,并在分束镜处合束,被分束镜反射的光进入光栅光谱仪,由光谱仪记录信号。由于光栅具有色散作用,因此进入光谱仪的“白光”将会在空间上分为各色“单色光”,这些单色光虽然经历了相同的路程,但光程不一样,因此会分别发生干涉相长或者干涉相消现象[8]。由于引入了光谱仪,在光程差远大于白光相干长度时,在频谱域中能够观察到干涉现象。
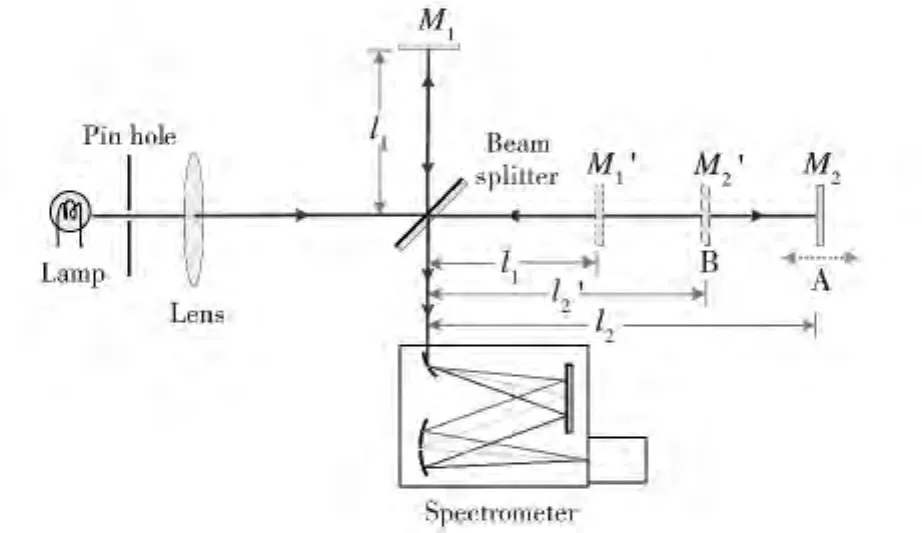
图1 白光频谱干涉光路示意图
在图1中,M'1为M1相对与分束镜BS分束面所成的像,假设白光光源的光谱分布为E0()λ,则从参考臂(竖直支路)和信号臂(水平支路)返回光的表达式 E1(λ,l1)、E2(λ,l2)可以写为:

光谱仪记录的光谱强分布I(λ)为:

其中Δ =2Δl=2( l2-l1)为两支路的光程差(不妨设l2≥l1)。
为了获得更加直观的白光频谱干涉信号图像,我们对(2)式进行数值模拟。为简化,假设E0(λ)=1,分束镜的分数比为1 1,反射镜的反射率为1,白光光源的波长覆盖范围为635 nm~655 nm,当光程差为1000μm,得到的频谱域干涉信号见图2,其中图2(b)为图2(a)中虚线框内的局部放大图。

图2 数值模拟得到的白光频谱域干涉条纹
由模拟使用白光光源的波长覆盖范围可以计算得到其相干长度为20.8 μm,由于光程差远大于其相干长度,因此在时域中是看不到干涉现象发生的,而在频谱域中却可以得到对比度极好的干涉信号。从(2)式可以看出,光谱仪记录的频谱干涉信号是受E0(λ)调制的、自变量为(1/λ)的余弦函数,其频率为Δ。同时从图2中可以发现,信号强度随波长(频率)发生近似正弦、余弦变化,这正是频谱干涉[2]的得名原因。
按照图1所示光路,搭建了实验系统,获得的典型频谱干涉信号如图3所示,其中图3(b)为图3(a)中虚线框内的局部放大图。对比图2、图3发现,实验得到的信号与模拟信号非常一致。
2 白光频谱干涉在微位移测量中的应用
通过图1所示的光路,假设得到的频谱干涉信号中λ1、λ2为两相邻波长(不妨设λ1> λ2),当λ1为m级干涉极大时,λ2为 m+( )1级干涉极大,则有:

从(3)式中可以解出m,并m将代入(3)式中,从而得到M'1与M2之间的距离为:
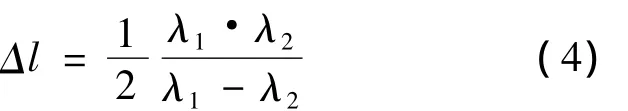
从(4)式可以得到M'1与M2之间距离测量误差以及相对测量误差为:

在搭建的实验系统中,光谱仪采谱的中心波长为644 nm,单次采谱范围35 nm,平均每2.37 nm产生一个条纹,取光谱仪的波长测量精度0.05 nm作为波长测量的误差,则利用(4)式进行简单计算得到M1'与M2之间的距离为87 313 nm,利用(5)式得到距离的测量误差为±14 nm,相对测量误差为±0.016%。为了使得测量结果更加准确,可以找出干涉信号中所有干涉极大值的位置,利用(4)式分别计算得到与该极大值对应的Δl,最后取所有Δl的平均值作为最后的实验结果。
在进行微位移测量时,只需分别记录M2移动前后的频谱干涉信号,并计算M1'与M2之间的距离 Δl、Δl',Δl与 Δl'的差值即为 M2移动的距离(displacement)。
将M2安装在一个电动平移台上,沿水平光路可前后移动,平移台标称单步移动距离为50 nm,实验中每移动10步后,进行采谱。为了减小随机因素的影响,电动平移台每移动一次后采5幅干涉信号分别进行计算,取其平均值作为最后得到的数据,实验获得的位移随移动步数的结果见图4。
对实验数据进行线性拟合,得到电动平移台的单步移动距离为48.9 nm,与其标称值基本一致,从而也说明白光频谱干涉法在微位移测量方面具有极高的测量精度。
3 白光频谱干涉与迈克尔逊干涉的比较
(1)白光频谱干涉采用了迈克尔逊光路,但采用的光源为钨灯,干涉信号的记录采用的是光谱仪,并且信号臂与参考臂中均未引入补偿片。
(2)白光频谱干涉光源的光程差远远大于其相干长度时,仍然能观察到干涉信号,因此光路中无需补偿片,这是与时域迈克尔逊干涉最重要的区别之一。
(3)白光频谱干涉在距离、位移测量上是一种绝对测量,即实验中无需导轨,无需实时记录或观测。在迈克尔逊实验中,需要保证信号支路的反射镜沿光路缓慢移动,以便保证不遗漏“冒出”或“缩进”的干涉条纹个数。
(4)白光频域干涉在距离、位移上有极高的测量精度,可以达到纳米量级,远高于迈克尔逊干涉法。
4 小 结
白光频谱干涉和传统的白光干涉、迈克尔逊干涉有着本质的不同,具有以下鲜明的特点:
(1)它把几何光学的若干内容和物理中的干涉很好的结合了起来,为通过实践认识干涉现象提供了条件,特别适合作为综合性实验或者专业课实验供高年级、学有余力以及对实验特别有兴趣的学生做。
(2)实验训练内容丰富,涉及到平行光的获取,光路调水平以及专业性仪器光谱仪的使用,综合性要求高,需要学生认真思考,动脑才能完成,任何一个环节的疏忽可能得不到干涉信号,这对严格进行实验的基本功训练是很有帮助的。
(3)该实验需要的白光光源(采用钨灯即可)、反射镜、分束镜等在一般大学物理实验室均可找到,光谱仪在专业实验室也是较为常用的仪器。
(4)由于当光程差远远大于相干长度时仍然能观察到干涉信号,当实验学生通过自己的努力获得干涉信号时,不仅得到了一次严格的实验基本功训练,也会有一种开阔眼界的新奇感和成就感。使得同学们从一个全新的角度重新认识干涉现象,有助于提高其对干涉知识掌握程度,激发大家的积极性及创新能力。
[1] 叶玉堂,肖峻,饶建珍,等.光学教程[M].北京:清华大学出版社,2011:157-161.
[2] 黄江.一个新颖的白光干涉实验的开发与研究[J].大学物理,2009,28(8):39-41.
[3] 贺水燕,高志峰.白光干涉实验探讨[J].大学物理实验,2002,15(4):28-30.
[4] 郭立群,赵英.迈克尔逊干涉实验中的三个问题[J].大学物理实验,2002,15(2):40-45.
[5] Maruthi M.Brundavanam,Nirmal K.Viswanathan et.al.Nanodisplacement measurement using spectral shifts in a white-light interferometer[J].Applied Optics,2008,47(34):6334-6339.
[6] Moshe Ben-Chorin,Silvia Chuartzman and Yehiam Prior.Distance measurements using a noisy white light interferometer[J].Applied Physics Letters,1998,73(5):581-583.
[7] V.Nirmal Kumar and D.Narayana Rao.Using interference in the frequency domain for precise determination of thickness and refractive index of normal disperse materials[J].Journal of Optics Society of America B,1995,12(9):1559-1563.
[8] 段秀铭.迈克耳逊干涉仪的调节技巧及常见问题解析[J].大学物理实验,2014,2(17):52-55.
[9] 吕乃光.傅里叶光学[M].北京:机械工业出版社,2006,182-187.
