三线摆实验现象的分析

张持良，王吉有，郭子豪，张 兵

(北京工业大学，北京 100124)

三线摆作为测量物体转动惯量的有效工具常被应用于实验测量［1-3］，目前多数大学开设此类实验［4-6］。在小角度(一般小于5度)摆动情况下，摆动近似于简谐振动，利用三线摆相关仪器测出参数及周期，可计算出转动惯量的大小。实验时学生控制摆动角度范围不准、摆动圆盘偏心和空气阻力等均会导致实验误差。本文利用自己设计可以测量摆动角度的三线摆仪器，测量了10度到60度摆角摆动周期，对实验测量周期与理论周期进行了对比分析。

1 实验原理

在无阻尼情况下，在摆盘启动转动一定角度θ(t)后，可以推导出摆动周期的理论公式［2］:

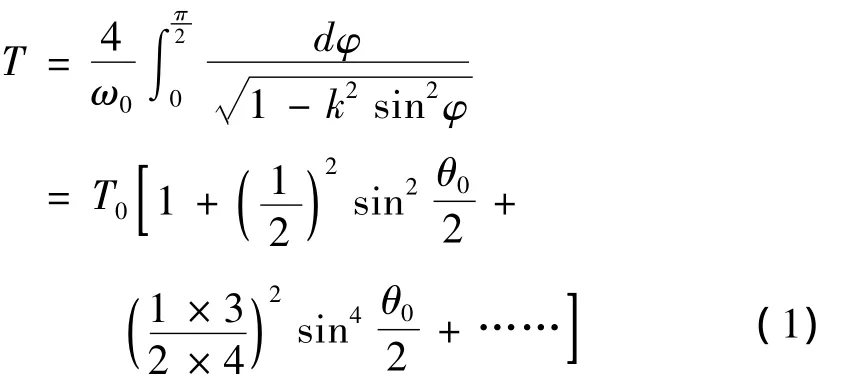
其中:T0为小角度下(近似简谐振动时)的摆动周期，θ0是摆动角。T0=4π2H/(Im0gRr)，H 是上下盘之间的垂直距离，r是上盘圆心到悬点半径，R为底盘圆心到悬点半径，g是重力加速度，m0是底盘的质量，I是底盘沿中心轴转动的转动惯量。

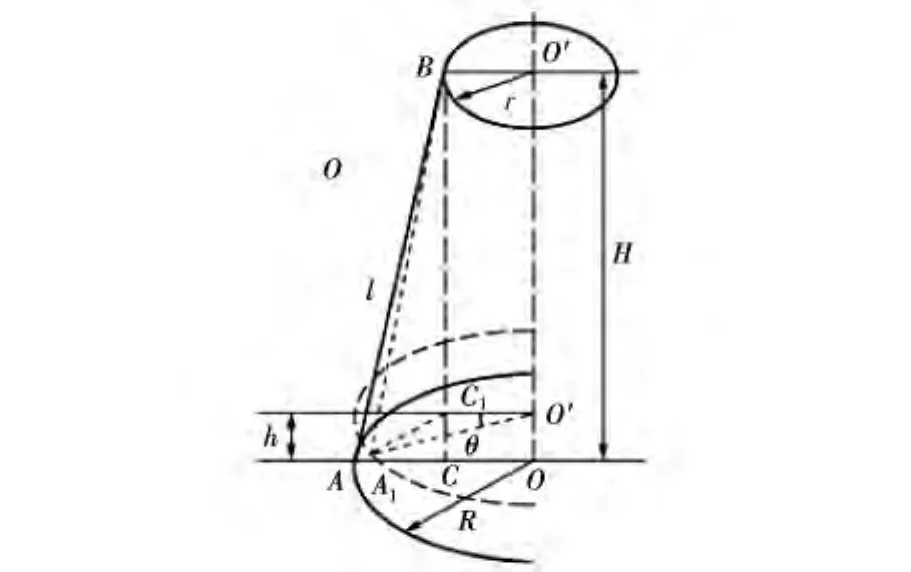
图1 三线摆几何分析图

2 实验数据和分析

2．1 摆动周期的理论值与实验值的对比研究

我们对上海天欣科教仪器有限公司生产的FD-IM-II型新型转动惯量测定仪进行了改进，制作增加了有机玻璃角度仪，以测量不同摆动角度下的周期，使用matlab软件计算了公式(1)在不同角度下的理论摆动周期值，利用计算和测量数据绘制了图2。其中T为理论周期，T1为实验测量周期。实验中三线摆的参数为:底盘的直径D=16．84 cm，上下盘之间的垂直距离H=49．9 cm，上盘圆心到悬点半径r=3．03 cm，底盘圆心到悬点半径R=8．03 cm，底盘的质量m0=601．78 g 。带入计算得到T0=4π2H/(Im0gRr)，理论值T0=1．693 s。

图2 三线摆摆动理论周期T、实测周期T1与角度的关系

从图2可以看出，随着摆动角度的增加，摆动周期变大，这主要是摆动运动已经不是周期不变的简谐振动。随着摆动角度的增大，摆动的理论周期与实测周期误差也不断增加，当摆动角度在35°以内时，摆动的理论周期与实测周期的相对误差小于千分之五，见图3。

图3 实验周期对理论周期的相对误差与摆角的关系

2．2 摆动过程中的平动分析

采用上文相同装置，先把摆盘扭到某个固定角度，然后释放，并开始计时。由于计时器显示的是整周期完成时的时间，而不是连续变化的时间，所以我们采用对计时器录像的方式进行数据记录，通过分析计时器的计时录像，记录出31个相邻而且连续增加的完整摆动周期。我们测出摆盘转动角度分别为 10°，15°，20°，25°，30°，35°，40°，45°，50°，55°，60°摆盘摆动2n次时对应的Tn(第n次摆盘的摆动周期)，通过画图分析，都发现随着摆动时间的变化，三线摆的摆动周期在缩小，摆动角在减小。此外，还发现摆动周期并不是连续的变小，而是呈周期性的变化并减小。

图4是摆盘释放起始角为60°时的周期数据，观察图像可以看出单个摆动周期值与周期序数关系图呈衰减波形，从实验上可以观察到这是由摆盘的平动引起的，由于摆盘平动，使得触发时间计数的摆线也平动，导致测量周期的变化。平动周期可用相邻波峰间的横轴距离表示。用同样的方法，我们 又 记 录 了 10°，15°，20°，25°，30°，35°，40°，45°，50°，55°(由于周期的衰减，9°以下的数据将不能完整精确测出，故最小测量角度定为10°)的周期值与周期序数关系。

图4 60度摆角起始时摆动周期与周期数的关系

为减小阻尼对实验的影响，在平动周期的数据分析中我们均取第一个完整平动周期(统一设定“波峰—波谷—波峰”为一周期)数据进行计算。由图4可以看出，三线摆一个平动周期由若干个摆动周期组成，平动周期值即为第一个完整平动周期曲线对周期序数n的积分，用这种算法，我们可以近似计算出不同角度下的摆盘平动周期。保持实验装置其他参数不变，由实验得不同角度下平动周期值，见表1(用Tp表示平动周期值)。

我们发现三线摆的摆动周期和平动周期都与摆盘的摆动起始角有关，所以我们假设一个平动周期与摆动周期的比值参数，用ρ表示ρ=Tp/T，从表1看到，不同摆动起始角的时ρ值比较相近，计算得ρ的平均值为5．011，故可得在我们实验条件下，三线摆近似平动周期公式Tp=5．011×T(T为三线摆转动周期)。

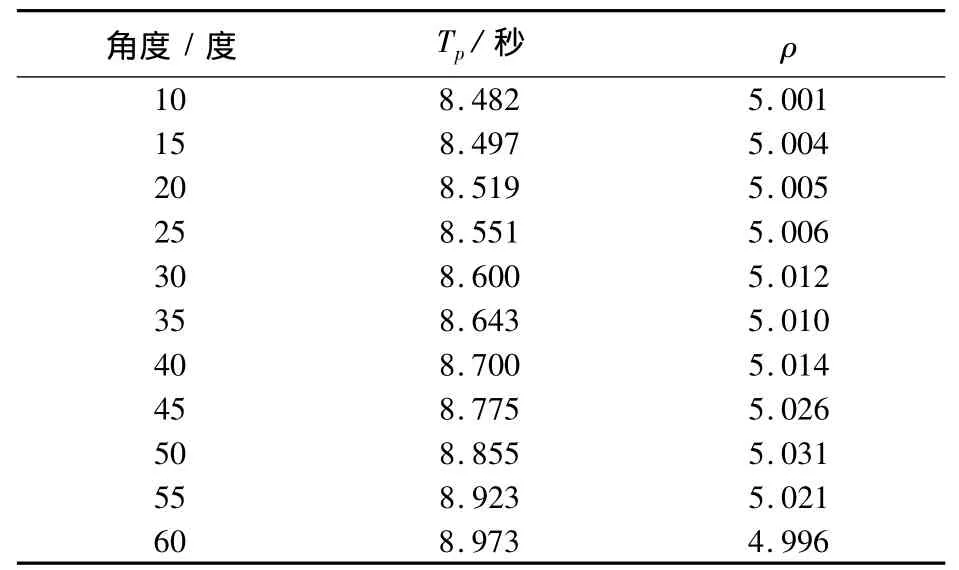
表1 三线摆平动周期与角度的关系

由于实验中的平动不可避免，所以学生在进行三线摆测转动惯量时，摆动周期的测量次数至少要包括一个平动周期，最好是2个平动周期，即测量10个摆动周期的平均值。

2．3 有阻尼情况下转动周期修改近似公式

利用上述三线摆阻尼分析实验数据进行处理，容易看出图4中的波形递减是由阻尼引起的。为方便观察阻尼大小，我们列出了不同摆动起始角的每条阻尼曲线在完整平动周期内的摆动周期平均值(T1表示第一个平动周期内的转动周期平均值，T2、T3、T4、T5、T6类推)，见表 2。

表2 因阻尼影响不同角度下摆动周期

将每一角度下的摆动周期TN进行直线拟合，从线性相关系数分析得出:大角度下，线性度很好，摆动周期随着摆动次数而线性减小，摆动起始角越小，阻尼现象越弱。

3 结 论

通过拉格朗日方程得出了大角度下三线摆周期与摆动角度的关系公式，并进行实验测量分析，发现摆角越大，相对误差越大。在实验中发现了无法避免的摆盘的平动，计算得平动周期约为摆动周期的5倍。研究了阻尼对摆动周期的影响，发现摆动周期随着摆动次数而线性减小，摆动起始角越小，阻尼现象越弱。由于实验中的平动不可避免，所以建议:学生在利用三线摆测转动惯量时，摆动周期的测量次数至少要包括一个平动周期，最好是2个平动周期，即测量10个摆动周期的平均值。

［1］ 李刚常，陈玉坤，余征跃．用三线摆测定物体对非质心轴的转动惯量［J］．力学与实践，2007，29(5):54-57．

［2］ 葛宇宏．长摆线三线摆大摆角摆动测定刚体转动惯量［J］．机械科学与技术，2010，29(6):792-796．

［3］ 董英伟．三线摆测刚体的转动惯量问题讨论［J］．天津职业技术师范学院学报，2001，11(3):35-37，61．

［4］ 邓金祥，刘国庆，等．大学物理实验［M］．北京:北京工业大学出版社，2011:79-83．

［5］ 陈群宇，姚列明，霍中生，等．大学物理实验［M］．北京:电子工业出版社，2003:93-96．

［6］ 吴波，朱瑜，左安友．三线摆转动角度控制装置的设计［J］．大学物理实验，2013(2):31-32．