基于主成分分析法的油料保障能力评估
2014-07-03舒先胜丁泽中夏亦寒詹启东
舒先胜,丁泽中,夏亦寒,颜 青,詹启东
(后勤工程学院,重庆 401311)
现代战争油料消耗品种多,数量大,油料保障影响作战进程和结局。搞好油料保障能力评估,对于掌握油料保障能力现状,寻求提高油料保障能力的有效途径,提高油料保障决策水平,具有重要现实意义。油料保障能力受诸多因素的影响,对其进行评估也有多种方法。主成分分析法是把原来多个变量通过降维化为几个综合指标的一种多元统计评估方法,该方法由于消除了评估指标之间相关关系的影响,在确保信息损失最小的前提下,以少数几个综合变量取代原始多维变量,方法较为简洁,结果比较客观,成为一种运用广泛的评估方法。
1 油料保障能力评估指标体系的建立
评估指标是评估专家评判油料保障能力的重要依据,指标选择的好坏对油料保障能力评估有重要影响。因此,建立油料保障能力评估指标体系应遵循一定的原则。
1.1 油料保障能力评估指标体系建立的原则
1)时效性原则。评估指标的建立必须根据当前油料装备、人员素质、保障机构设置等实际情况,充分考虑油料保障能力基本要素和油料保障外部环境对油料保障的影响,建立适应当前油料保障工作实际的指标体系。
2)系统性原则。油料保障能力的形成是多种因素共同作用的结果,因此,必须用系统的眼光来思考评价指标的选取,要在纵向上形成多层次结构,在横向上形成发散型结构,确保评价指标能全面反映油料保障能力。
3)动态性原则。油料保障能力是在动态中释放和显现的,因此,评估指标的建立既要参考当前油料保障系统实际,又要考虑其未来的发展趋势和需求,设置部分超前性的指标,确保指标体系在一定时期内相对稳定。
4)简明性原则。指标数量既不能过多也不能太少,能基本满足评估要求和决策需要即可;要突出主要指标,减少重复指标;指标要便于获取,易于测量,具备较强的可操作性,以方便评估的进行。
5)独立性原则。各个指标之间的相关性要小,要尽量减少指标间的交叉,避免出现指标间的相互包含,使每个指标在评估体系中具有相对的独立性。
1.2 指标体系的建立
油料保障能力评估指标体系可以按照油料保障能力的构成要素、环节、归属等方法建立,形成层次型的评估指标体系。本文按照油料保障能力构成要素建立指标体系,即用油料保障人员、油料保障机构、油料保障装备、油料保障信息、各种油品等要素来评价油料保障能力。具体指标体系如表1所示。

表1 油料保障能力评估体系
2 主成分分析法的运用步骤
主成分分析又叫主分量法或主轴分析,其基本方法是通过构造原变量适当的线性组合,产生互不相关的新变量,然后从中选出少数几个含有较多原变量信息的新变量,并用这几个新变量代替原变量进行分析和解决问题。其运用步骤为:
步骤1 采集样本矩阵并对其标准化
运用专家咨询法采集p 维随机向量x =(x1,x2,…,xp)T的n 个样本xi=(xi1,xi1,…,xip)T,i=1,2,…,n,n >p,构造出原始样本矩阵X。
采用Z-score 法对矩阵X 进行标准化处理,以消除各指标因属性不同引起的差异,得到标准化矩阵Z,处理方法为

步骤2 求矩阵Z 的相关系数矩阵R

步骤3 求矩阵R 的特征值与特征向量
解矩阵R 的特征方程

可得其p 个非负特征值λ1>λ2>… >λP>0,从而得到对应于λj的p 个单位特征向量,构成一个正交矩阵,记为b。
步骤4 计算主成分的数值(即主成分得分矩阵)
对全部n 个样本,有

其中U 为样本主成分矩阵。
步骤5 根据主成分贡献率选择主成分
由R 的特征值λj,可求得第k 个主成分的贡献率为

前m 个主成分的累计贡献率为

以累计贡献率不低于85%确定主成分的个数。
步骤6 计算主成分综合评估值,并进行排序:
以各主成分的贡献率作为权重,线性加权求和得到主成分的表达式

其中Fi反应了第i 个单位m 个主成分的贡献率,Fi值越高,表明该单位m 个主成分的重要性越高,反之越弱。
以每个主成分对应的特征值占所提取主成分总的特征值之和g 的比例作为权重计算综合主成分得分评估值

其中F 为n 个样本的综合评估值,以此进行排序和评价。
3 油料保障能力评估实例分析
下面以15 个油料保障单位为例,运用主成分分析法对其油料保障能力进行评估。
为获得原始样本数据,根据油料保障能力评估体系,运用专家咨询法对这些单位进行评估,如表2 所示。
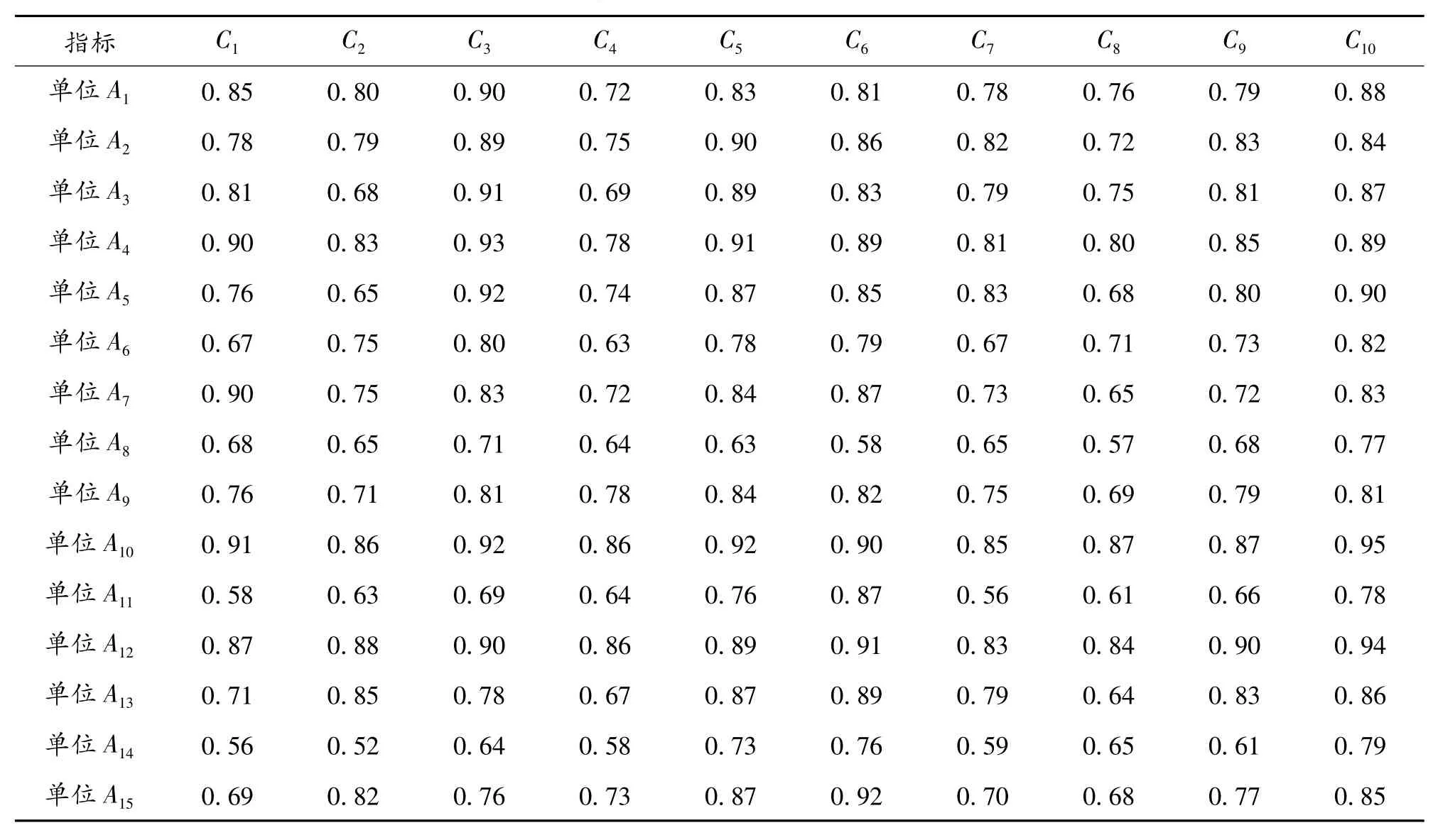
表2 各单位评估指标
表2 中各单位Ai对指标Cj的样本属性值为xij,据此构造出原始样本矩阵X= ( xij)15×10,采用Z-score 法对X 进行标准化,得到标准化矩阵Z=(zij)15×10,由式(1)可求得Z 的相关系数矩阵R=(rij)10×10,由式(2)可求得R 的特征值λj,由式(4)、式(5)可得各个特征值的贡献率和累计贡献率,如表3 所示。
从表3 可以看出,前两个特征值的累计贡献率已达到85.02%,符合不小于85%的要求,因此取前两项主成分就可满足决策需要。由式(2)可求得λj所对应的单位特征向量b,再由式(3)可求得样本主成分得分矩阵U 为


表3 R 的特征值及贡献率
由式(6)可得前两个主成分分量的表达式为

由式(7)可得综合评估值F 为

由此可得到各单位的综合评估排名,根据排名高低可以看出各个油料保障单位的综合保障能力大小,如表4 所示。
从综合排名情况看,单位10 的油料保障能力最好,而单位14 的油料保障能力最差。由综合评估模型F 进一步分析得出,C1、C2、C6所占权重较高,说明油料保障人员的满编率、称职率及油料保障装备的完好率对单位的油料保障能力影响较大。指挥员可根据评估结果采取相应对策,重点加强油料保障人员和保障装备建设,从而不断提高油料保障能力。
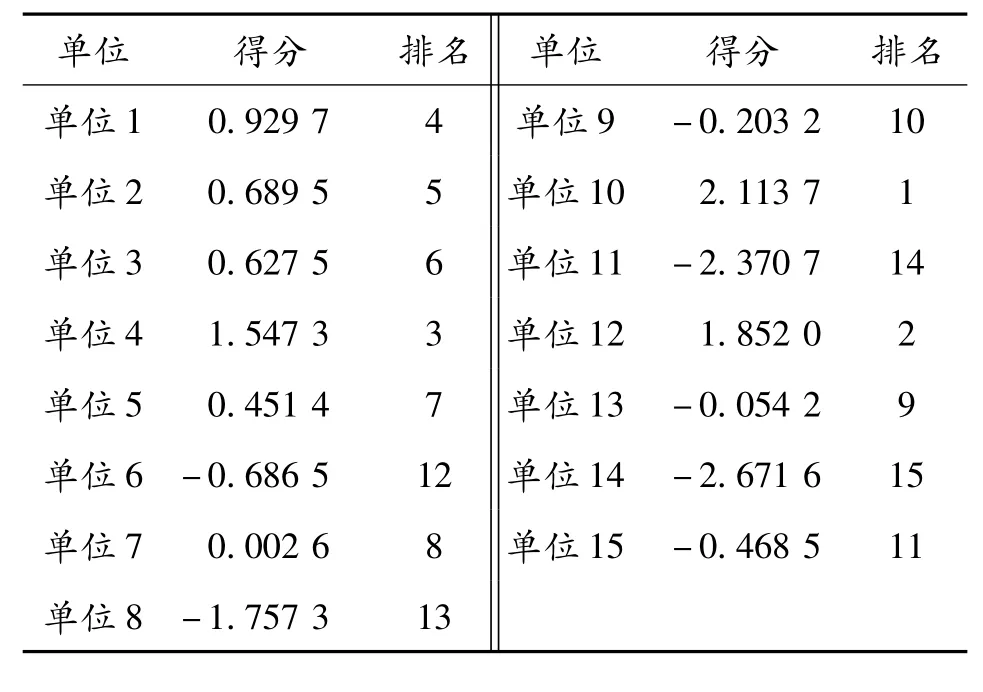
表4 各单位综合评估得分排名
[1]马亚龙,邵秋峰.评估理论和方法及其军事运用[M].北京:国防工业出版社,2013.
[2]王海涛,阳平华.基于主成分分析法的装备维修资源保障能力评估[J].四川兵工学报,2008(4):30-32.
[3]秦寿康.综合评价原理与应用[M].北京:电子工业出版社,2003.
[4]侯进军,肖艳清.数学建模方法与应用[M].南京:东南大学出版社,2012.
[5]周庆忠. 军队油料勤务[M]. 北京: 国防工业出版社,2008.
[6]李柏年,吴礼斌.MATLAB 数据分析方法[M].北京:机械工业出版社,2012.
