基于电路模型的弹射用永磁无刷直流直线电机参数优化及仿真
2014-07-03汤子鑫姬新阳孙思浩林炜庭
汤子鑫,姬新阳,孙思浩,林炜庭
(1.总装备部南京军事代表局 驻福州地区军事代表室,福州 350003;2.中国洛阳电子装备试验中心,孟州 454750)
电磁弹射[1-3]用永磁无刷直流直线电机在工作过程中,电压高、电流大,要求推力恒定,速度动态范围大,末速度能达到几十甚至上百米每秒,对推力波动、位置精度要求相对较低。因此,电磁弹射用直线电机参数的选择,要结合电磁弹射的特点,在传统的方法基础上进行改进、修正。
文献[4]中采用有限元的方法对转矩波动进行优化,对于弹射用电机,难度增大,考虑的因素更多。对推力波动的分析,考虑电机工作在稳态,速度是恒定的,没有考虑速度的影响,不适合用于弹射用电机分析[5-6]。文献[7-9]中对推力波动进行了优化,采用的控制算法并未深入分析速度对推力的影响,其控制在低速效果较好,在高速时还需改进,并且在高速时闭环控制可能因为换相时间过长而不能使用。
文中结合电磁弹射的特点,推导出换相推力波动、非换相期间推力波动、效率公式,并以此为目标函数建立了矢量优化模型。采用词典排序算法解决了多目标之间冲突问题,对单个目标函数采用模拟退火算法进行优化求解,最后在Matlab 环境下进行了仿真验证。
1 永磁无刷直流直线电机数学模型
永磁无刷直流直线电机采用方波供电,三相星型六状态工作方式。为方便分析,作如下假设:
1)三相对称,反电动势为梯形波,平顶部分等于120°电角度;
2)忽略电枢反应、齿槽效应、端部效应和磁路饱和的影响;
3)相绕组的等效电感为常数;
1.1 换相过程的数学模型
换相过程[10]以A 相为例,从A 相关断开始,到A 相电流降为零,此过程的等效电路如图1 所示。
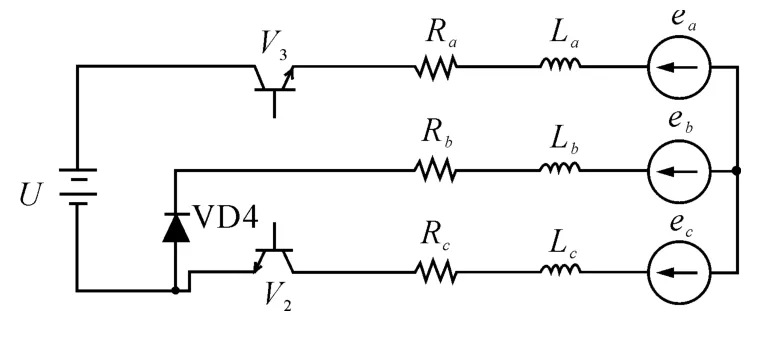
图1 换相期间电机等效电路
在换相期间,直线电机的数学模型为
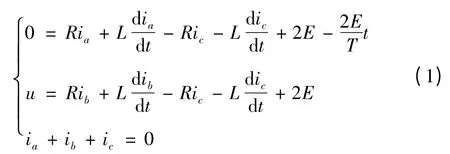
在B/C 相导通的换流过程中,三相绕组的反电动势分别为
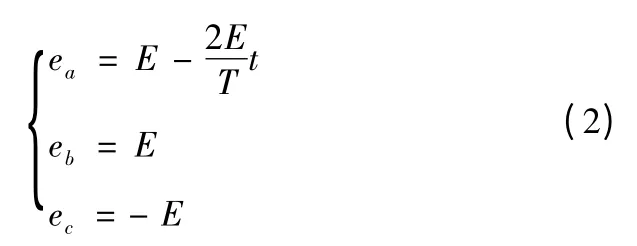
其中E=kv,k 为绕组反电动势系数。
其中R 表示绕组电阻,ia、ib、ic分别表示相电流,L 表示绕组等效电感,u 为端电压。
永磁无刷直流直线电机的推力方程为
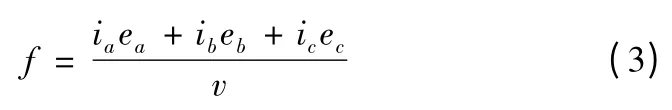
推力波动定义为
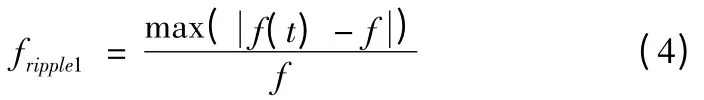
其中f(t)为换相期间的推力,f 为弹射过程要求的推力。
联合式(1)~式(4)得到换相推力波动为
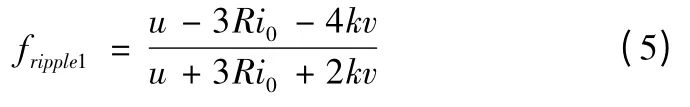
1.2 非换相过程数学模型
在非换相期间,任意时刻只有两相导通,第三相截止。导通两相绕组上的反电动势大小相等,方向相反;电流大小相等,方向相反。不考虑非导通相续流的影响,采用PWM 调制方式,以A、B 两相导通为例,其等效电路如图2 所示。
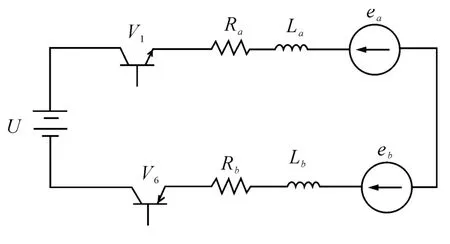
图2 简化的等效电路
其数学模型为
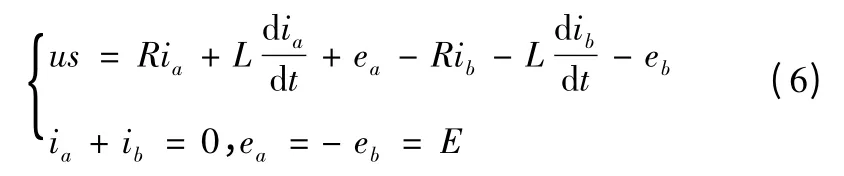
当PWM 信号为ON 时,s =1;当PWM 信号为OFF 时,s=0。u 为端电压,v 为电机运动速度,反电动势与速度的关系E=kv,k 反电动势系数。
结合永磁无刷直流直线电机非换相期间推力波形特点,定义推力波动为
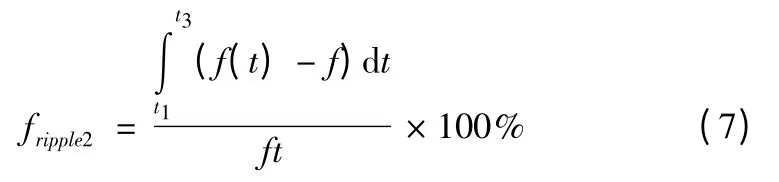
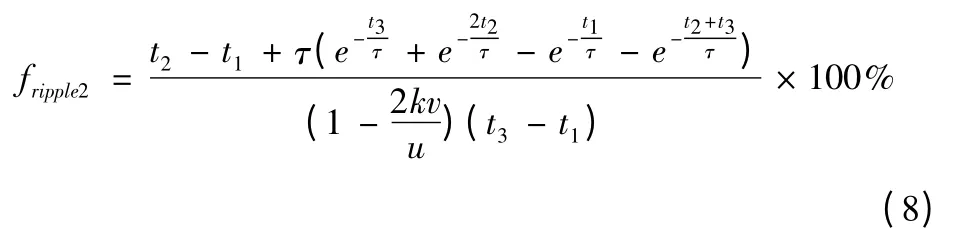
结合式(6)和式(7)得其中,推力波动的计算在一个PWM 周期下,对应的时间区间为[t1,t3],PWM 信号为OFF 时对应的区间[t1,t2],PWM 信号为OFF 时对应的区间为电磁时间常数。
2 弹射过程电流、电压分析


在换相期间,其初始电流为非换相期间结束时的电流,因此换相期间初始电流为换相时间很短,假设在换相期间电压大小不变,电压大小为非换相结束时的电压。
将式(9)和式(10)代入换相期间推力波动式(5)和非换相期间推力波动式(8),得到在电磁弹射过程中的推力波动公式分别为
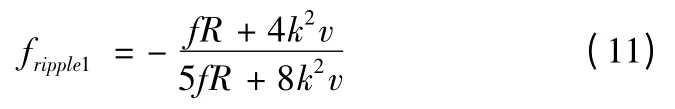
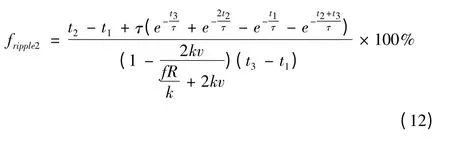
3 电机参数优化
对于优化问题,从3 个方面进行分析,目标函数、约束条件、最优解的计算方法。
3.1 目标函数的确定
对于非换相期间推力波动,推力增大,推力波动减小,速度增大,推力波动增大。因此,只选一组推力和速度是不能代表整个系统的推力波动。为了能更好地反应速度和推力对换相推力波动的影响,选择多组推力和速度。以多组推力和速度的换相推力波动之和作为优化目标函数
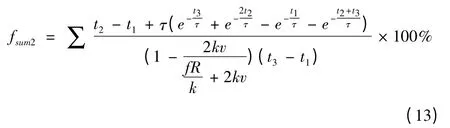
换相推力波动的分析方法与非换相期间推力波动类似,以多组推力和速度的换相推力波动之和作为优化目标函数
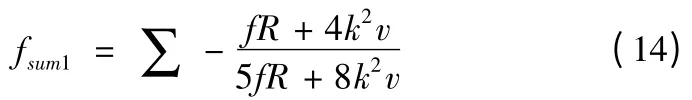
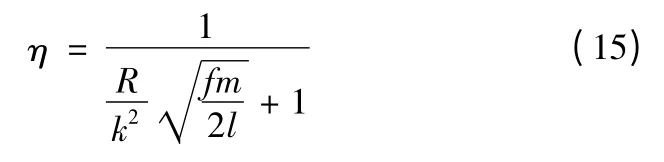
以电机效率最高为第三个目标函数。
3.2 约束条件
换相过程中,任何速度下的换相推力波动要满足系统的要求,即

在非换相过程中,同时对于每个速度,推力波动要满足系统的要求
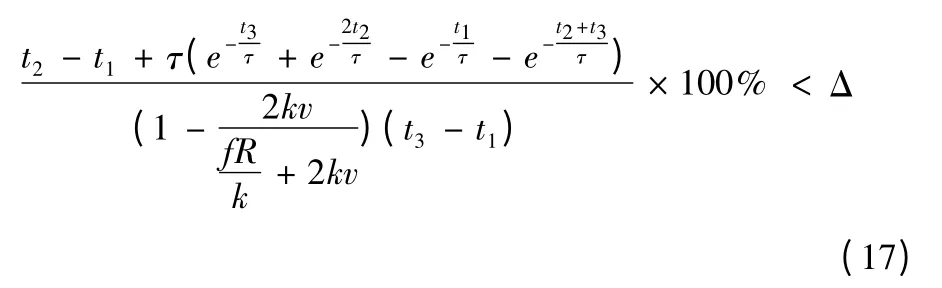
其中Δ 为系统要求的推力波动大小。
在电磁弹射过程中,由于受器件及各种因素的影响,电流和电压的大小被受到限制,因此工作电流和电压要小于系统的要求。
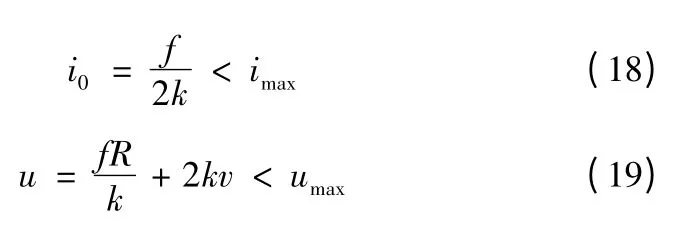
在实际中,各相参数的取值是受到限制的,为了减小计算量,获得优化的解,对电感、电阻、反电动势系数进行约束,根据实际情况,给出电感、电阻、反电动势系数的数值范围
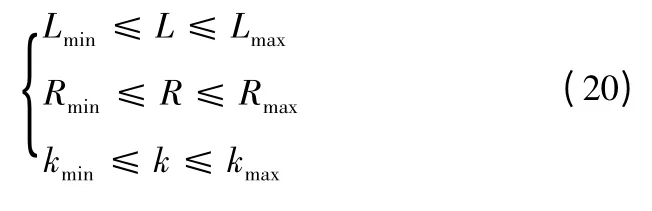
3.3 参数求解
对于矢量优化问题,解决的方法很多,如加权极小极大最优值法、基于性别辨识的矢量遗传算法、词典排序算法、随机权系数和优等个体法、基于接触理论确定Pareto 最优解方法等。在文中采用词典排序算法(Lexicographic Ordering),其原理是根据目标函数的重要性进行排序,先对最重要的目标函数进行寻优,然后根据目标函数的重要性依次进行,最终求的最优解。
本文中的3 个目标函数,重要性依次为非换相期间推力波动最小、换相推力波动最小、效率最高。对于每一个目标函数,对应的优化模型属于非线性优化问题,一般的解析方法过于复杂。可采用粒子群、模拟退火、遗传算法等智能随机搜索算法,在本文中采用模拟退火算法。
Metropolis 等人在1953 年提出了模拟退火算法Simulated Annealing Algorithm(SA),基本思想是把优化过程与统计热力学的热平衡问题进行对比,固体退火过程的物理图像和统计特性是模拟退火算法的物理背景,Metropolis 接受准则使算法跳离局部最优的陷阱,冷却进度表的合理选择是算法应用的前提。固体退火是先将固体加热至溶化,然后徐徐冷却使之凝固成规整晶体的热力学过程。具体算法实现过程如下:
1)以最小非换相期间推力波动为目标函数,采用SA 进行优化;
2)以最小换相推力波动为目标函数,利用第一步中求的最优解,将非换相期间推力波动等于该最小值作为约束条件,采用SA 进一步优化;
3)以最高效率为目标函数,将第二步中最小换相推力波动等于最小值作为约束条件,其他约束条件不变,利用SA求得最优解,此时的最优解为矢量优化目标的最优解。
对于每一个目标函数f(x)的优化,采用模拟退火算法,具体过程如下:
1)参数初始化,首先给出被优化参数(电阻、电感、反电动势系数)的取值范围,即解空间为= L,R,( )k ⊂[ LminLmax]× [ RminRmax]× [ kminkmax]。控制参数的初始值T 及衰减系数λ,内循环次数Ns,步长向量=[v1,v2,v3],终止规则(精度值ε 及温度最小值Tm);初始化搜索点x0,计算f0=f),令=。
3)计算f ' =f(x'),如果f '≤fi,则接受新解,令如果f ' >fi,以概率p = exp接受新点x'(Metropolis 准则),在新解'被接受的情况下,令
4)h=h+1,如果h <Ns,转到步骤2,否则h=1,转到下一步。
5)减小控制参数Tk+1=λTk,如果Tk+1<Tm,则算法终止,否则重复步骤2)到4)。
4 参数优化与仿真
电机参数优化时选择推力分别为1 500 N、2 000 N、2 500 N、3 000 N、3 500 N、4 000 N;速度取值选择为5 m/s,10 m/s,15 m/s,20 m/s,25 m/s,30 m/s,35 m/s;非换相推力波动要求小于10%,换相推力波动要求为小于30%,因为换相推力波动还可以通过各种控制方法进一步减小,而非换相推波动要进一步减小非常复杂;最大电流为imax=300 A,最大电压umax=1 500 V;电感参数区间 2,[ ]20 ,单位mH,电阻取值区间 1,[ ]10 ,单位Ω,反电动势系数的取值 5,[ ]20 ,单位V×s/m,占空比0.9。
分别以非换相推力波动、换相推力波动、效率为目标函数进行优化,计算结果如下:
以非换相期间的推力波动为目标函数,得到最优参数为:r=3.429,k=8.247,L=5.87;
以换相期间推力波动为目标函数得到最优参数为:r =6.533,k=5.122,L=18.2;
以效率为目标函数,优化后得到:r =1.636,k =12.551,L=7.13。
其中,以效率为目标函数得到的参数即为矢量目标函数的最优参数,所以电机的最优参数为r =1.636,k =12.551,L=7.13。
为了验证理论分析的正确性,以负载30 kg,推力2 000 N,末速度要求35 m/s,加速距离为其效率为对位移区间5 ~5.5 m 进行推力仿真。
图3 为未进行抑制时的换相推力波动,推力波动达到20%。采用提前换相抑制方法,换相推力波动减小到10%以内,如图4。
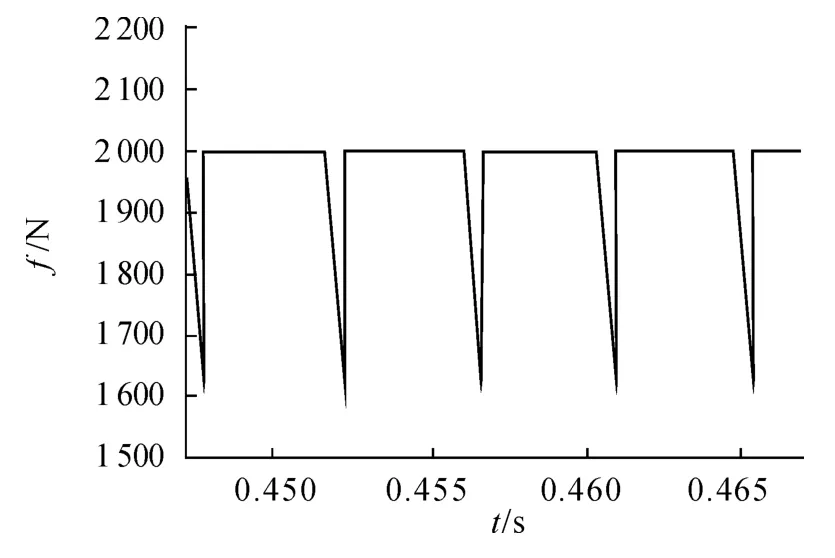
图3 直接换相时的推力
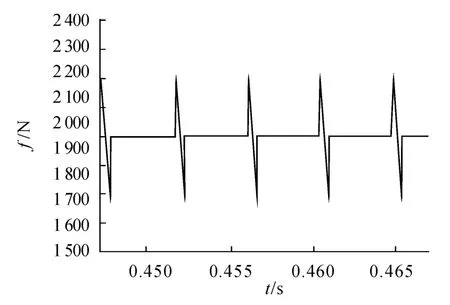
图4 抑制后的换相推力
图5 是电机在5 ~5.5 m 时的推力曲线,其中非换相期间推力波动较小,而换相推力波动较大,所以在对推力波动抑制中,重点考虑换相推力波动。
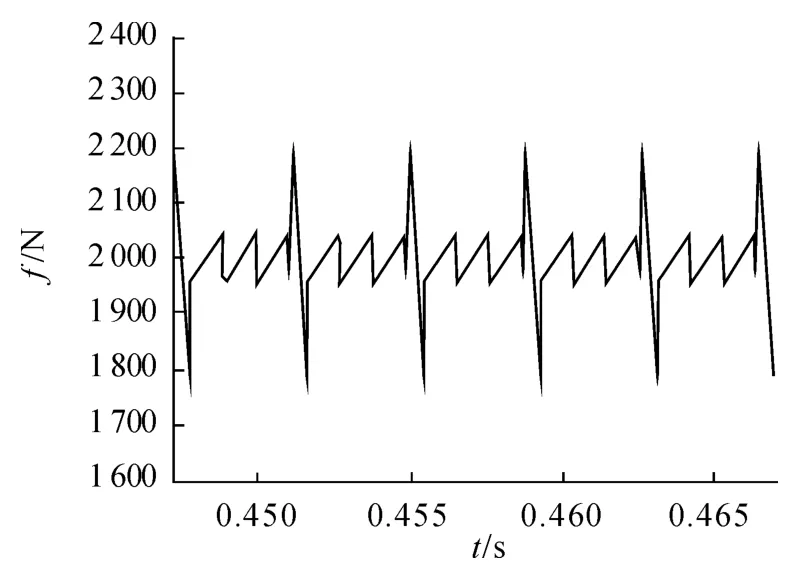
图5 5 ~5.5 m 的推力曲线
5 结束语
在换相期间和非换相期间数学模型基础上,推导出推力波动公式。结合电磁弹射的特点,分析得到换相期间和非换相期间以推力和速度为自变量的电流及电压表达式。并将电流电压公式代入到非换相推力波动、换相推力波动及效率的表达式,得到新的表达式,并依此为目标函数,建立矢量优化模型。采用词典排序法解决多目标之间的冲突问题,对于每一目标函数的优化,采用模拟退火算法。求解模型获得电机参数,并通过MATLAB 仿真验证了理论分析的可行性,从得到的结果中看出,电机本体优化对换相推力波动减小是有限的,还需通过电机控制进一步减小换相推力波动以满足系统的要求。
[1]李立毅,李小鹏.电磁发射的历史与发展趋势[J].微电机,2004,37(1):41-44.
[2]Doyle M,Sulish G,Lebron L.The benefits of electromagnetically launching aircraft[J]. Naval Engineering Journal,2000,112(3):77-82.
[3]吴始栋.美国海军电磁弹射器现状[J].船电技术,2005(3):5-6.
[4]Ohnishi T,Takahashi N. Optimal design of efficient IPM motor using finite element method[J].IEEE Trans.Magn.,2000,36:3537–3539.
[5]S. M. Hwang,D. K. Lieu. Reduction of torque ripple in brushless DC motors[J].IEEE Trans.Magn,1999,31(2):3737-3739.
[6]Min Dai,Ali Keyhani. Torque ripple analysis of a PM Brushless DC Motor using finite element method[J].IEEE transaction on energy conversion,2004(19):40- 45.
[7]Zhu Z Q,Howe D.Influence of design parameters on cogging torque in permanent magnet machines[J]. IEEE Trans.Energy Conversion,2000(15):407–412.
[8]Yong Liu,Zhu Z Q,David Howe. Direct torque control of brushless DC drives with reduced torque ripple[J]. IEEE transaction on industry applications2005,41(2):599-608.
[9]Xia C L,Guo P J,Shi T N,Speed control of brushless DC motor using genetic algorithm based on fuzzy controller[C]//IEEE international conference on intelligent mechanics and Automation Japan.[S. l.]:[s. n.],2004: 460-464.
[10]Zhu Z Q.Direct torque control of brushless DC drives with reduced torque ripple[J].IEEE transactions on industry applications,2005,41(2):599-605.
