基于遗传算法优化BP神经网络的供暖系统热负荷预测模型

2014-07-03张经博王朝霞

兵器装备工程学报 2014年4期

张经博，郭凌，王朝霞，刘凌

(1.后勤工程学院，重庆 401311;2. 65133 部队，沈阳 110000;3.重庆大学，重庆 400000;4.重庆工程职业技术学院，重庆 400055)

供暖系统的热负荷与室外温度、太阳辐射、风向和风速等气候条件关系密切。热负荷预测主要是指根据以往热负荷温度的实际情况，同时考虑影响热负荷温度相对权重较高的因素，如室外温度、日照时长、工作作息情况等因素，对未来某一时间段内或某一具体时刻的需求量作出估计或范围性推测，从而实现对供暖系统辅助决策的数据支持;预测精度不够高是现有预测模型的主要缺点，同时供暖系统的供暖量的变化波动大时自适应能力较差［1］。根据供暖系统对热负荷预测的预测精度要求高的实际需求，本文提出的预测模型是针对下一个工作日的短期热负荷预测，主要选择了前3个工作日的负荷温度、室外温度、日照时长作为输入参数;本文提出的基于遗传算法(genetic algorithm，GA)优化的BP 神经网络(back propagation neural network)对供暖系统热负荷预测，将遗传算法自适应性和全局优化能力强的优点，和BP神经网络局部寻优能力强的优点相互结合，从而避免了BP神经网络容易陷入局部极小的缺点，大大提高了预测的精度，从对比仿真实验可以验证提出的方法的误差比BP 神经网络预测出的误差要小。

1 遗传算法

1.1 遗传算法的基本原理

遗传算法(genetic algorithm，GA)是一种基于自然选择和基因遗传学原理的优化搜索方法，是模拟达尔文的遗传选择和自然淘汰的生物进化原理被引入到待优化参数形成的编码串群体中，按照选取好的适应值函数和一系列的遗传操作对个体进行筛选，从而保留下适应值高的个体，组成新的群体。通过这种方式产生的新群体不仅遗传了上一代的大量信息，而且包含优于上一代的新个体。这样一代一代遗传下去，群体中个体的适应值不断提高，直至满足一定的条件为止。

遗传算法是从一个种群开始的，这个种群代表了问题的一个可行解。而种群则由一定数目的个体组成，每个个体通过基因编码产生。在生物学里，每个个体是带有特征的染色体实体。由于染色体是多个基因的集合，所以首先要进行编码，把表现型编码成基因型。在每一代的进化中，个体的选择是由种群中的个体适应值大小来决定的，由遗传算子进行组合、交叉和变异，产生出新的种群。这个过程使种群像遗传选择和自然进化一样，让新种群更加适应于环境，不适应的种群逐步被淘汰，直到产生出最优种群或达到迭代次数后形成末代种群，末代种群中的最优个体经过解码，就可以作为问题近似最优解。

1.2 遗传算法的操作

Holland 的遗传算法［2］，通常称为简单遗传算法，主要特点是操作简单和作用强大，基本遗传操作如下:

1)选择操作

选择操作是指以一定概率选择旧种群中的个体到新种群中，个体被选中的概率跟适应值有关，个体适应值越大，被选中的概率就越大。

2)交叉操作

交叉操作是指从种群中选择两个个体，通过两个个体的染色体的交叉组合，来产生新个体。交叉过程为从种群中任选两个个体，随机选择个体的一点或多点染色体位置进行交换。交叉操作如图1 所示。

图1 交叉操作

3)变异操作

变异操作是指从种群中任选一个个体，选择个体的染色体中的一点进行变异产生新个体。变异操作如图2 所示。

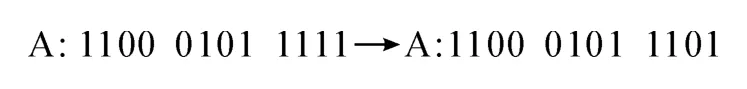
图2 变异操作

2 遗传算法优化BP 神经网络

由于BP 神经网络局部寻优能力强，但缺点是易于陷入局部极小;遗传算法则具有自适应性、全局优化性和隐含并行性，但缺点是局部寻优能力不强。本文提出了一种BP 神经网络与遗传算法相结合的算法，用遗传算法优化BP 神经网络的权值和阈值，解决BP 神经网络易陷入局部极小的问题，然后利用优化后的权值和阈值经过BP 网络训练来得到最优解［3］。

遗传算法优化BP 神经网络分为BP 神经网络结构确定、遗传算法优化和BP 神经网络预测3 个步骤。其中，BP 神经网络结构确定由问题和拟合函数的参数个数决定的，进而遗传算法个体的长度才能得以确定;遗传算法优化是利用遗传算法对BP 网络的权值和阈值进行优化筛选，由于种群中的每个个体都包含了一个网络所有权值和阈值，通过适应度函数计算出每个个体的适应值，通过遗传算法的选择，交叉和变异等操作后找到最优的适应值所对应的个体;BP 神经网络预测是指通过遗传算法筛选出最优个体，然后将最优个体赋值给BP 网络初始权值和阈值，BP 网络基于初始权值和阈值进行训练后得到预测输出。从而使新生成的算法既要有神经网络的强自学习能力，又有遗传算法的强全局搜索能力［4］，其算法流程图如图3 所示。

通过遗传算法来优化BP 神经网络的初始权值和阈值，同时提高神经网络的泛化性能，是遗传算法优化神经网络的主要方法，通过遗传算法优化后的BP 神经网络，具有更好的预测输出结果［5］，遗传算法优化BP 神经网络的具体实现步骤如下:

1)种群初始化

每个个体按照实数进行编码，每个遗传个体由一个实数串组成，可分为输入层与隐含层的连接权值、隐含层阈值、隐含层与输出层连接权值以及输出层阈值4 个部分，它与某个神经网络权值、阈值、隐节点一一对应。在网络结构已经确定的情况下，就组成了一个权值、阈值和结构都确定的BP 网络，同时每个个体包含了BP 网络全部的权值和阈值［6］。

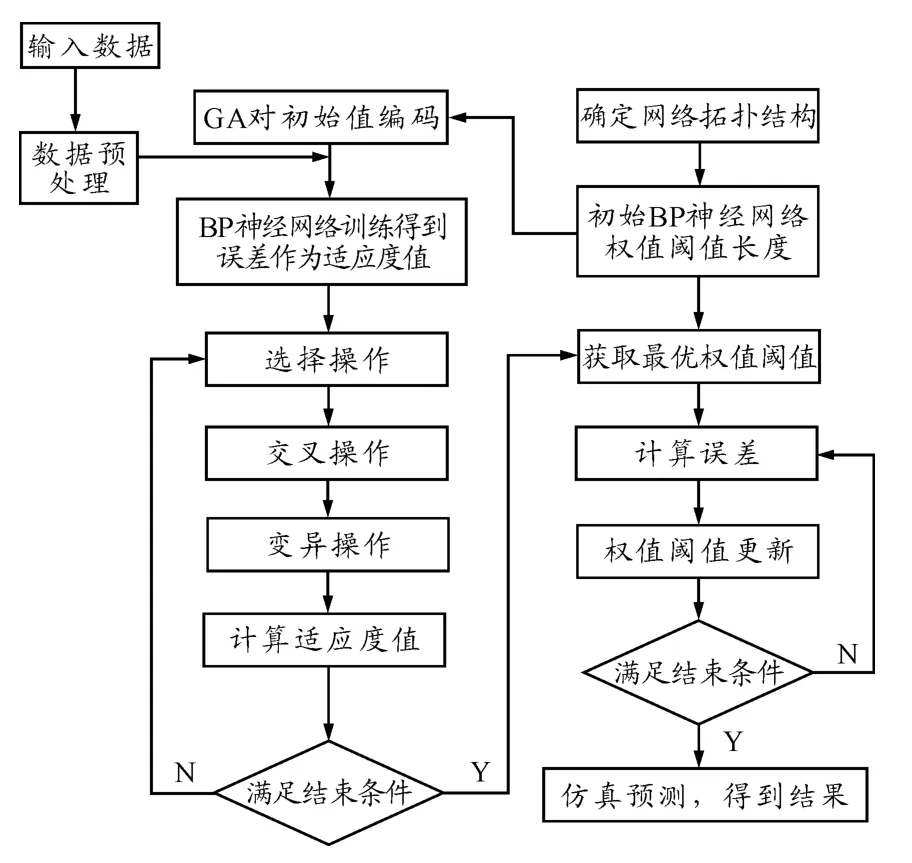
图3 遗传算法优化BP 神经网络算法的流程

2)适应值函数计算

根据种群初始化得到的BP 神经网络的初始权值和阈值［7］，这样就避免了BP 神经网络随机生成初始权值和阈值的随机性，避免了BP 网络容易陷入局部极小的缺点，同时利用训练数据对BP 神经网络进行训练，训练后的BP 神经网络预测出输出结果，可将预测输出值和期望输出值之间的平方误差和作为个体的适应值F

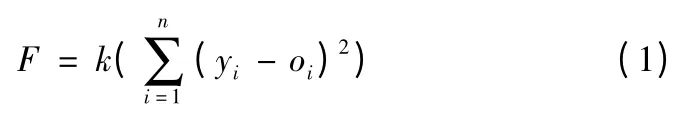
式中:n 为网络输出节点数;yi为BP 神经网络第i 个节点的期望输出;oi为第i 个节点的预测输出;k 为系数。

3)选择算子

本文的遗传算法选择操作是以轮盘赌法［8］为基础，即基于每个个体的选择概率等于其适应度与整个种群中个体适应度和之比的选择策略，个体适应度越高，被选中的可能性就越大，进入下一代的概率就越大。定义每个个体i 的选择概率pi

式中:Fi为个体i 的适应值，由于适应值越小越好，所以在个体选择前对适应值求倒数;k 为系数;N 为种群个体数目。

4)交叉算子

交叉算子主要包括单点交叉、多点交叉、均匀交叉、算术交叉、启发式交叉等，由于个体采用实数编码，所以交叉操作方法采用实数交叉法，第k 个染色体ak和第l 个染色体al在j 位的交叉操作方法如下:

式(4)、式(5)中，b 为［0，1］间的随机数。

5)变异算子

将父代群体中的每个个体以某种概率(即变异概率)改变某个个体的某些基因座上的基因值为其他的等位基因。对每次变异的结果，还原出神经网络并进行性能评估。如果后代优于父代则结束该父代的变异，否则，对该父代进行下一次变异，直到找到优于其父代的后代。

变异操作是对实数编码选取第i 个个体的第j 个基因aij进行变异，变异操作方法如下

式中:amax为基因aij的上界;amin为基因aij的下界;f(g)=r2(1-g/Gmax);r2为一个随机数;g 为当前迭代次数;Gmax是最大迭代次数;r 为［0，1］之间的随机数。

6)结束

根据网络训练后得到的误差，如果误差满足要求，或者达到一定的进化代数，则进化停止;否则返回步骤(3)。

3 仿真实例

这里分别用BP 神经网络和遗传算法优化BP 神经网络2 种方法对供暖系统热负荷进行预测。通过对影响热负荷变化的各种因素进行分析，发现可能的输入变量有:在供暖系统方面，供水流量、供水温度、回水温度等;在外部条件方面，室外温度、风速风向、太阳照射率、气压等，在时间性方面，是否工作日、白天还是晚上等［9］。根据数据获取的难易程度和数据来源情况，本文在选择影响供暖负荷的输入变量时，综合考虑、简化各输入变量，最后确定将是否工作日、室外温度、日照时数和前3 天的负荷温度等6 个影响因素作为输入变量。

热负荷预测模型的输出变量的选取是根据系统不同的运行方式来选择的。一般情况下的控制方式主要有2 种:一是以控制回水压差为主的控制方式，采用这种控制方式的供暖系统预测模型一般选择供回水压差作为输出变量;另一种是以控制温度为主的运行方式，一般选择供回水温度作为输出变量。本论文针对的是以控制温度为主的供暖系统，因此把供水温度，也就是负荷温度作为输出变量。

本文对收集的500 个供暖系统热负荷样本数据进行学习和预测，其中400 个样本数据作为学习样本，另外100 个样本数据作为预测样本［10］。部分输入样本如表1 所示。

为了避开Sigmoid 函数的饱和区域，使输出量随着输入量的变化较为明显，在仿真实验中，先对样本数据作归一化处理。本文选取的BP 神经网络为3 层，网络为6-5-1 结构，输入层有6 个节点，隐含层有5 个节点，输出层仅有1 个节点。本文的BP 算法采用L-M 算法，学习率选为0.1。在遗传算法的优化过程中，种群规模取40，最大进化代数取80［11］。

表1 部分输入样本

用遗传算法优化BP 神经网络算法对400 个学习样本数据进行训练［12］，得到的训练结果如图4 所示。其中遗传算法的优化过程如图5 所示。

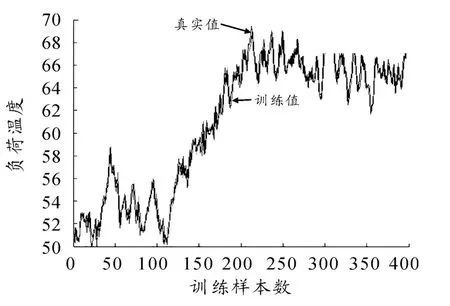
图4 遗传算法优化BP 神经网络的训练结果

由图4 可知其算法的训练误差为294.958 3。用训练好的网络对100 个预测样本进行预测［13］，其预测的结果如图6所示。

其预测得到的绝对误差［14］结果为73.965 3，相对误差结果为0.017 3，如图7 和图8 所示。

图7 遗传算法优化BP 神经网络的预测结果的绝对误差

图8 遗传算法优化BP 神经网络算法的预测结果的相对误差

作为对比试验，用BP 神经网络对400 个学习样本数据进行训练［15］，得到的训练结果如图9 所示。

图9 BP 神经网络算法的训练结果

由图9 可知其算法的训练误差为305.109 8。用训练好的网络对100 个预测样本进行预测，其预测的结果如图10所示。

图10 BP 神经网络算法的预测结果

其预测得到的绝对误差结果为85.232 7，相对误差结果为0.019 7。

由上面的实验结果可看到，遗传算法优化的BP 神经网络算法的训练结果的误差比BP 神经网络算法的训练结果的误差要小，遗传算法优化的BP 神经网络算法的预测结果的绝对误差和相对误差也比BP 神经网络算法的训练结果的误差要小。其原因是BP 算法容易陷入局部极小点，而遗传算法搜索的是全局极小点，所以遗传算法优化的BP 神经网络算法要比BP 神经网络算法得到更好的训练结果，其预测结果也更好，如表2 所示。

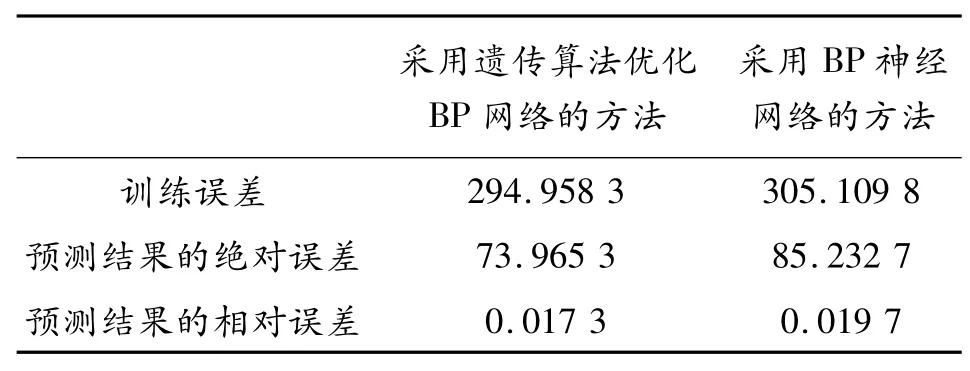
表2 两种方法的误差对比表

4 结束语

本文针对供暖系统热负荷短期预测问题，利用改进的遗传算法对BP 神经网络的初始权值和阈值进行优化，并在遗传进化过程中采取保留最佳个体的方法。该方法克服了一般BP 网络初始权值的随机性和网络结构训练过程中的所带来的网络震荡，以及一般BP 网络容易陷入局部极小等问题。从以上的结果分析可知，对于供暖系统热负荷短期预测，本文所采用的遗传算法优化的BP 神经网络具有全局寻优能力，预测精度高，绝对和相对误差较小，收敛速度快，能够有效针对供暖系统热负荷进行短期预测。

［1］康胜文.两种热负荷预测方法的比较［J］. 区域供暖，2004（2）:22-24.

［2］李敏强.遗传算法的基本理论与应用［M］.北京:科学出版社，2002.

［3］王崇骏，于汶滌，陈兆乾，等.一种基于遗传算法的BP 神经网络算法及其应用［J］.南京大学学报:自然科学版，2003（5）:459-466.

［4］周明，孙树栋.遗传算法原理及应用［M］.北京.国防工业出版社，1998:11-12.

［5］刘严崴.基于神经网络的供热系统负荷预测［D］.天津:天津大学，2009.

［6］杨梅，卿晓霞，王波.基于改进遗传算法的神经网络优化方法［J］.计算机仿真，2009（5）:198-201.

［7］唐丽杰.城市供暖系统的数据采集与算法研究［D］.济南:山东轻工业学院，2007.

［8］雷英杰，张善文，李续武，等. 遗传算法工具箱及应用［M］.北京:中国水利水电出版社，2005.

［9］欧阳玉梅，马志强，方若森.基于MATLAB 的遗传神经网络的设计与实现［J］.信息技术，2008（06）: 73-76.

［10］彭岚，何大鹏，李友荣.基于BP 神经网络的工业锅炉房负荷预测［J］.工业加热，2006（5）: 31-33.

［11］陈路路.基于负荷预测的集中供热系统能效研究［D］.济南:山东建筑大学，2013.

［12］李超.基于自适应遗传算法的BP 神经网络预测研究及应用［D］.西安:陕西师范大学，2012.