基于优先级的建筑外表面光伏电池铺设优化模型

马翠，敖翔，庞剑飞，刘志敏

(1.第三军医大学a.数学与生物数学教研室;b.学员旅5营，重庆 400038; 2.中国人民解放军73232部队卫生队，浙江舟山 316217)

基于优先级的建筑外表面光伏电池铺设优化模型

马翠1a，敖翔1b，庞剑飞2，刘志敏1b

(1.第三军医大学a.数学与生物数学教研室;b.学员旅5营，重庆 400038; 2.中国人民解放军73232部队卫生队，浙江舟山 316217)

建筑外表面光伏电池的铺设直接影响到其发电总量。首先对不同光伏电池的经济效益进行分析并将其作为电池的选择优先级，确定了房屋外表面铺设各型号光伏电池的选择优先级序列;而后基于选择优先级序列，采用剩余矩形匹配算法对光伏电池的选择及铺设方式进行计算，获得光伏电池铺设方案，从而建立基于优先级的建筑外表面光伏电池铺设优化模型;最后，运用2012年全国大学生数学建模竞赛相关数据对模型进行验证。结果表明:模型所确定的最优光伏电池铺设方案符合实际，经济效益大，具有较好的通用性和推广价值。

太阳能;光伏电池;铺设方案;优先级;剩余矩形匹配算法

太阳能是世界上最丰富的能源，将太阳能转化为电能具有巨大的发展潜力，有望在不远的未来解决现今的能源危机问题［1］。目前，在利用光伏电池实现太阳能发电的过程中，光伏电池是指通过光电效应或光化学效应直接把太阳能转化为电能的装置。常用的光伏电池有单晶硅电池、多晶硅电池和非晶硅薄膜电池3种类型［2］。为减少用地，光伏电池常铺设在建筑物外表面(即光伏建筑)。由于房屋外表面面积一定，故如何挑选光伏电池并尽量铺满外表面从而使发电量最大便成为一个亟需解决的问题。本文基于优先级的思想建立了房屋外表面光伏电池优化铺设模型，并运用2012年全国大学生数学建模竞赛B题的相关数据对该模型进行验证，结果表明所建模型能较好地解决实际问题。

1 光伏电池铺设优化模型的建立

在建筑外表面铺设光伏电池时，需要解决电池种类的挑选以及外表面尽量铺满这两个问题。对于前者，按照发电量尽可能大、单位发电量的费用尽可能小的要求，计算出每种型号光伏电池在某面墙的太阳辐射总强度下的经济效益，并以此作为各型号光伏电池对于该面墙的选择优先级，获得光伏电池选择优先级序列;对于后者，考虑到一般房屋外表面与光伏电池均为矩形，故利用剩余矩形匹配算法获得外表面光伏电池最大铺满方案。据此思路，本文建立了光伏电池优化铺设模型示意图，见图1。

1.1 建筑外表面逐时太阳辐射总强度的计算

一般气象站台提供的气象数据都是水平面上逐时太阳总辐射强度的数据，但光伏电池面常为倾斜面，关于倾斜面上逐时太阳总辐射强度的计算，本文按照现阶段国际惯例，采用Klien和Theilacker提出的计算方法［3］:倾斜面上的太阳总辐射强度HT由直接太阳辐射量Hbt、天空散射辐射量Hdt和地面反射辐射量Hrt3部分组成，并认为天空散射辐射量呈均匀分布。其计算公式如下:

式(1)中:¯R为倾斜面上逐时平均太阳辐射量与水平面上逐时平均太阳辐射量的比值;¯Hd为水平面上逐时平均散射辐射量;¯H为水平面上逐时平均总辐射量;β为倾斜面倾角;ρ为地面反射率，一般情况下，ρ=0.2;D为取值函数，其表达式及相关参数意义详见文献［3］。

图1 光伏电池优化铺设模型

对于赤道朝向的倾斜面，上述计算过程可简化。在北半球，其逐时平均太阳总辐射量与水平面上逐时太阳平均总辐射量之比为

建筑外表面的逐时辐射总强度H(t)为

1.2 光伏电池选择优先级序列的求解

在实际情况中，常要求光伏电池发电总量尽可能大，而单位发电量的费用尽可能小，满足这两者的直观表现为经济效益最大。故本文选取各型号光伏电池的经济效益作为其相应的选择优先级。

为方便计算各种型号光伏电池在某墙面光照条件下的选择优先级En，假设该外表面上全部安装此型号的光伏电池，并求得在其使用寿命范围内所获得的经济效益，以此作为En，其计算方式如下:

式(4)中:m1为居民电价;S为外表面的面积;Sn为某型号光伏电池的面积;表示商值取整;l为光伏电池的最大使用寿命;ηn为某型号光伏电池的转化效率。需要说明的是，不同种类的光伏电池有其特异的转化效率计算方式，在实际中，ηn视情况而定;mn为某型号光伏电池的单块价格。

根据上式可求得各型号光伏电池在某墙面光照条件下的选择优先级En，将其按照降序排列，即得到该建筑外表面的光伏电池选择优先级序列E。

1.3 基于光伏电池选择优先级序列的剩余矩形匹配算法对光伏电池最大铺满问题的求解

由于房屋外表面与光伏电池形状一般均为矩形，故考虑使用剩余矩形匹配算法求解光伏电池最大铺满问题。但在本模型中强调优先级思想的应用，故此处需对剩余矩形匹配算法进行修正，获得基于光伏电池选择优先级序列的剩余矩形匹配算法，以对最大铺满问题进行求解。

剩余矩形匹配算法［4－5］采用矩形集合Rj记录放入零件j(第j次放入的零件)时材料所有可利用的区域，每个零件在排样前都与矩形集合Rj中各个矩形区域进行匹配度fjk计算(下述)，依次将零件放入与之匹配度最大的矩形区域。具体过程如下:

以矩形的左下角和右上角坐标记录矩形的位置，并用rjk表示Rj中第k个矩形(［(xjk，yjk)，(Xjk，Yjk)］)，每次排样时均从剩余矩形的左下角放入，显然在放入第一个零件时初始集合R1中的可利用区域仅包含矩形板材即R1=r11［(x11，y11)，(X11，Y11)］。在放入零件2时剩余矩形集合中由于放入了零件1(宽w1，高h1，且w1≥h1)而形成了2个可利用的矩形区域;当横向排入(零件的宽与剩余矩形底边重合)零件1时，如图2所示，剩余矩形集合R2的计算公式为

竖向排入(零件高与剩余矩形底边重合)时，与图2类似，剩余矩形集合R'2的计算公式为

以此类推，每次将待排零件j(宽w1，高h1且w1≥h1)放入匹配度最高的剩余矩形rjk中，同时更新剩余矩形集合，除被选中的矩形k外其他矩形位置均不变，矩形k在被放入零件j后将产生2个新剩余矩形。当板材所有可利用的区域不能再放入零件时增加板材，令剩余矩形集合为初始集合R1，并重新开始排放剩余的零件。

图2 剩余矩形表示(横排)

结合本模型，在对每个墙面采用上述算法时，考虑到小屋某些墙面上有窗户、房门等空缺，故在设置算法初始条件时，就将这些空缺部分考虑成起始矩形。此外，根据已获得的房屋外表面的光伏电池选择优先级序列。本文定义匹配度fjk的公式为

式(7)中:Ek为第k个矩形光伏电池在光伏电池选择优先级序列中所对应的优先级;yjk为在房屋外表面以某一角为原点建立坐标系，第k个矩形光伏电池矩形左下角坐标的纵坐标。

2 实例运用

2012年高教杯全国大学生数学建模竞赛B题为太阳能小屋的设计问题，要求给出小屋外表面的光伏电池最优铺设方案。本文利用其提供的相关数据［6］，运用上述模型，给出题中太阳能小屋屋顶前斜面的光伏电池优化铺设方案。

根据上文所建模型，对B题所附数据利用Matlab2012a进行编程实现，可得屋顶前斜面的太阳逐时辐射总强度、光伏电池选择优先级序列以及优化铺设方案，如表1、2和图3所示。

表1 屋顶前斜面的逐时辐射总强度

表2 屋顶前斜面的光伏电池选择优先级序列

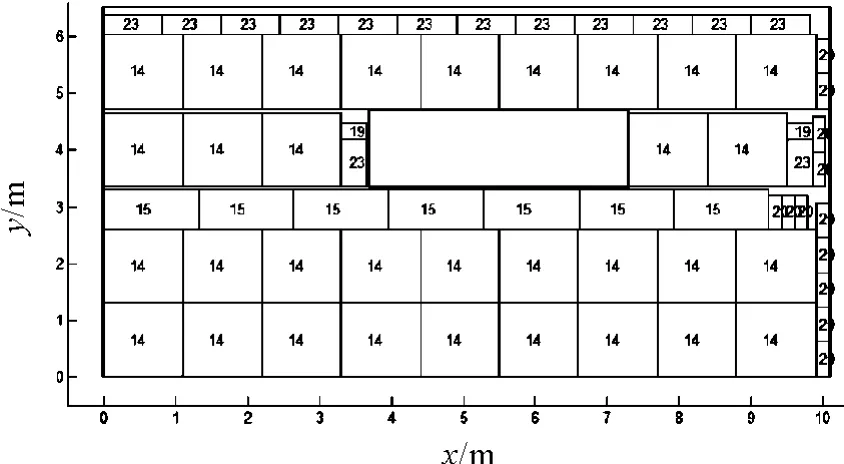
图3 屋顶前斜面的光伏电池优化铺设方案

利用本模型还可求得屋顶前斜面上光伏电池的投资与收益，见表3。

表3 屋顶前斜面上光伏电池的投资与收益

3 结束语

本文建立的基于优先级的建筑外表面光伏电池优化铺设模型，由于方法灵活且便于计算机编程实现，可广泛应用于建筑外表面光伏电池优化铺设问题的求解或对光伏发电系统的评价，具有较强的应用性和推广性。

［1］时艳侠，郭荣波，许晓辉，等.微藻太阳能电池的初步研究［J］.可再生能源，2009，6(3):15－17.

［2］袁镇，贺立龙.太阳能电池的基本特性［J］.现代电子技术，2007(16):163－165.

［3］Klien S A，Theilacker JC.An algorithm for calculating monthly－averse radiation on inclined surfaces［J］.Journal of Solar Energy Engineering，1981，103:2－33.

［4］曾凤华.剩余矩形匹配算法在矩形件排样中的应用［J］.机电工程技术，2006，35(3):64－65.

［5］杨威.板材排样优化的计算智能方法研究［D］.成都:四川大学，2002.

［6］全国大学生数建模竞赛组委会.2012年高教杯全国大学生数学建模竞赛赛题［EB/OL］.http://www.mcm. edu.cn/problem/2012/2012.html.

(责任编辑 杨黎丽)

Optim ization Model of the Building Outside Surface of Photovoltaic Cells Laying Based on the Priority

MA Cui1a，AO Xiang1b，PANG Jian－fei2，LIU Zhi－min1b
(1.a.Department of Mathematics and Mathematical Biology;b.The Battalion 5 of Cadet Brigade，Third Military Medical University，Chongqing 400038，China; 2.Medical Unit of 73232 of the PLA，Zhoushan 316217，China)

The roll－out of the building outside surface of photovoltaic cells directly affect its total power generation.In this paper，firstly，the economic efficiency of photovoltaic cellswas analyzed as the selection priority of cells，and the priority sequence of the photovoltaic cells laying on building outside surface was determined.Based on that，remaining rectanglematching algorithm for the selection and laying of the photovoltaic cells were calculated.The laying scheme of the photovoltaic cells was obtained，so as to establish the optimization model of the building outside surface of photovoltaic cellslaying based on the priority.Finally，the actual use of the 2012 CUMCM’s data proved that the optimum photovoltaic cells laying plan determined by the established model has good economic benefits and value of application and popularity.

solar power energy;photovoltaic cells;laying scheme;priority;matching algorithm of remaining rectangular

TK511

A

1674－8425(2014)09－0112－05

10.3969/j.issn.1674－8425(z).2014.09.024

2014－03－13

国家大学生创新创业计划(201390035019)

马翠(1982—)，女，硕士，讲师，主要从事数学建模及智能计算研究;通讯作者敖翔(1992—)，男，陕西安康人，主要从事数学模型的应用及其研究。

马翠，敖翔，庞剑飞，等.基于优先级的建筑外表面光伏电池铺设优化模型［J］.重庆理工大学学报:自然科学版，2014(9):112－116.

format:MA Cui，AO Xiang，PANG Jian－fei，etal.Optimization Model of the Building Outside Surface of Photovoltaic Cells Laying Based on the Priority［J］.Journal of Chongqing University of Technology:Natural Science，2014(9):112－116.