超分辨率图像恢复方法综述

向海燕

(重庆邮电大学信号与信息处理重点实验室，重庆 400065)

超分辨率图像恢复方法综述

向海燕

(重庆邮电大学信号与信息处理重点实验室，重庆 400065)

由于成像技术及工艺的限制，从硬件方面提高超分辨率需要花费高昂的费用，因此考虑从软件方面实现图像的超分辨率。对现有的超分辨率图像技术进行了介绍，然后在此基础上提出了算法的研究方向和展望，对超分辨率图像恢复技术的研究有一定意义。

超分辨率;高分辨率图像;低分辨率图像;图像恢复

图像超分辨率可以被理解为图像放大之后细节仍然清晰可见。现有的超分辨率图像恢复一般是指恢复出一幅图像边缘清晰，细节、轮廓等较为清晰、合理的算法。超分辨率恢复技术通过一幅或者多幅低分辨率图像，经由重建的方法来获得一幅高分辨率图像［1］。由于目前成像器件分辨率的限制，从硬件上提高图像的分辨率需要高昂的费用和代价，因此从软件方面来实现图像的超分辨率具有较大的研究意义和价值。

自Tsai和Huang［2］于1984年第一次提出超分辨率重建问题以来，出现了很多超分辨率恢复方法。超分辨率图像恢复方法主要分为3种:第一种是基于插值的超分辨率恢复算法;第二种是基于重建约束的超分辨率图像恢复算法;最后一种是基于学习的超分辨率图像恢复方法。基于插值的算法主要包括双线性插值，双三次插值等，算法简单但效果差，特别是当放大倍数较大的时候，重建效果会急剧下降。基于重建约束的超分辨率图像恢复算法是研究较多的算法，主要包括迭代反投影(IBP)［3］，最大后验概率大(MAP)［4］，凸集投影法(POCS)［5］等。这些方法在低分辨率图像足够多的情况下，只要低分辨率图像配准精度足够高就能恢复出具有较高质量的图像。基于学习的超分辨率图像恢复方法［6］是目前研究的热点和难点，它打破了奈奎斯特采样频率的极限，即使采样率小于等于2倍的奈奎斯特频率，仍然能够恢复出原始图像。而在基于学习的超分辨率算法中，基于稀疏学习的超分辨率图像恢复［7，13］是目前研究中效果最佳的算法，后续很多研究都是在此基础上进行扩展。

1 超分辨率图像恢复方法

图像插值技术是一种比较简单的数学问题，它是利用周围像素或者邻近点之间的关系对高分辨率图像网格中未知像素的估计，使得这个估计值接近最理想的结果。常见的插值算法有最近邻插值、双线性插值、三线性插值、以及样条插值和分形插值。插值技术比较简单，但是插值技术会因为放大因子的增大而出现立即下降的情况，因此很少考虑插值技术。下面主要介绍两种图像恢复的超分辨率技术:基于约束重建和基于学习的超分辨率图像恢复技术。

1.1 基于约束重建的超分辨图像恢复技术

实际应用中，所获得的低分辨率图像是由成像器件采集到的图像。而由于受成像器件的限制以及成像水平的影响，获得的图像一般是模糊、分辨率低且含有噪声的图像，故一般实现图像恢复算法采用的低分辨率图像都是将高分辨率图像经过退化模型模拟产生。

1.1.1 图像退化模型

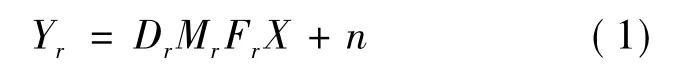
式(1)中:Dr为采样矩阵，大小为ab×q2ab，由于选择的采样率一样，所以直接用D表示即可;Mr为模糊矩阵，大小为q2ab×q2ab，模糊矩阵也是相同的，也用M表示;Fr为运动矩阵，大小为q2MN ×q2MN;n为噪声，和原始图像大小一样即为a× b，此处利用H=DMP来表示整个过程。超分辨率图像恢复就是在已知观测的一系列低分辨率图像的条件下，恢复出超分辨率图像，所以图像恢复是一个反问题，其求解是一个病态逆问题［8－9］。

1.1.2 对重建模型的求解

1)迭代反投影(IBP)算法

迭代反投影［10］是出现比较早的算法，它的基本思想是:首先通过插值方法估计出一幅高分辨率图像，之后利用通过下采样、模糊操作模拟低分辨率图像。迭代反投影就是利用模拟的低分辨率和给定低分辨率图像之间Y的差值来不断更新当前估算，而迭代操作过程中有一个反迭代矩阵HBP，它近似为H－1，即有

反迭代投影强调重建的结果要和原始的观测数据匹配，但是由于重建结果的病态问题的存在，重建的结果不是唯一的，且在IBP中没有加入先验知识，因此解的结果可能不稳定、不唯一，而且HBP的选择也是一大难点。

2)最大后验概率(MAP)

最大后验概率是在IBP出现之后发展起来的，最经典的算法是由Russell C.Hardie提出的MAP图像重建［11］。该算法对未知图像的估计是通过最大化给定的一系列观测图像Y对理想图像X的条件概率密度函数P(X|Y)而得到的，即有

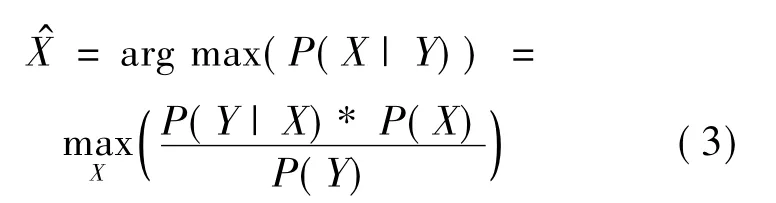
由于P(Y)与X是无关的，对上面取对数，因此可以简化为下面的式子:

从式(4)可以看出:该算法有效地利用了图像的先验知识，因此能对解进行约束，从而实现解的唯一。但是目前而言，图像的先验信息选取不准确会对图像的效果有很大影响，而且该算法的时间代价也较高，不利于视频和图像的实时处理。

3)凸集投影(POCS)

凸集投影［12］使用集合理论把需要恢复的图像的各种先验信息，例如正定、能量有界、数据可靠、光滑等定义为约束凸集，满足这些约束的值就是图像解集。POCS是一种迭代过程，在给定超分辨率图像空间中任意一点的前提下，它可以定位满足所有凸约束集条件的点，即收敛解。

POCS的解集是一个凸集，该凸集可以定义如下:

其中:yj(x，y)表示第j幅低分辨率图像的像素值; rj(x，y)表示残差;(x1，y1)表示高分辨率图像的估计;hj(x，y;x1，y1)表示对图像的下采样和模糊等操作。

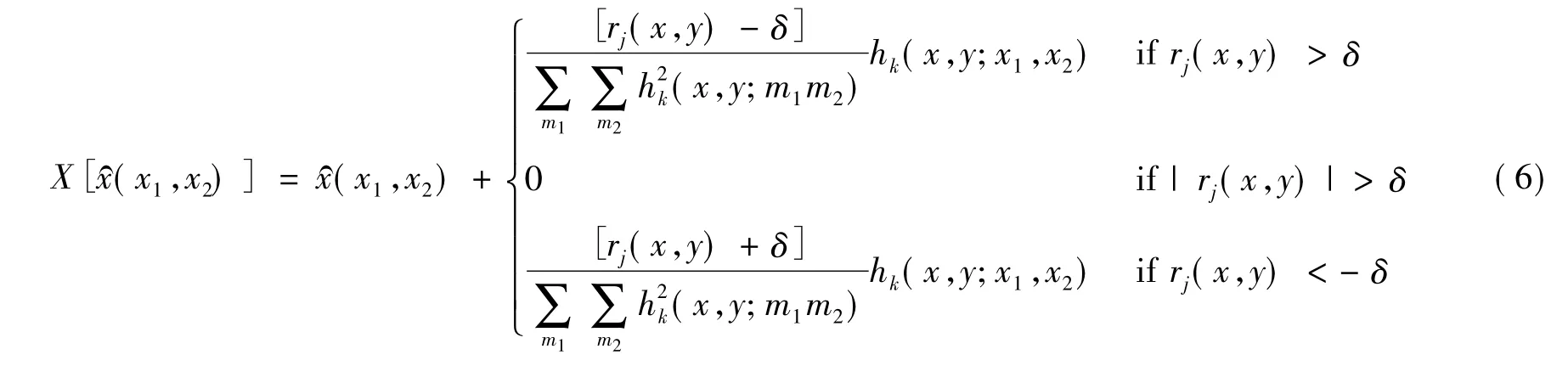
该方法没有唯一解，而且最后的解依赖图像的初始估计，具有收敛速度较慢且解不稳定等缺点。

1.1.3 小结

上面的方法各有优缺点，后续有很多研究给出了各种改进。改进后的图像效果和速度有所改善，但是当图像的放大因子达到饱和时，不论增加多少低分辨率图像都不能再改善图像的效果，因此基于学习的超分辨率图像恢复技术应运而生。

1.2 基于学习的超分辨率图像恢复技术

基于学习的超分辨率图像恢复技术是目前图像恢复技术研究的热点。它通过学习高、低分辨率图像块之间的关系，并将这个关系作为先验信息指导低分辨率图像进行重建，这个关系就是需要学习的。目前基于学习的方法大致可以分为两种:基于样本的方法和基于稀疏表示的方法。下面主要围绕这两种超分辨率图像恢复进行说明。

1.2.1 基于样本的超分辨率图像恢复方法

Freeman［13］于2002年首次提出基于样本的超分辨率方法。通过建立高分辨率块与对应低分辨率块和邻近块之间的关系，引入了马尔可夫先验场。其基本思想是:让每一个低分辨率图像块y成为一个观测节点，选择16个或者是与之非常靠近的样本作为隐藏节点x的不同状态，这个x就是需要估计的值。条件概率分布建模为

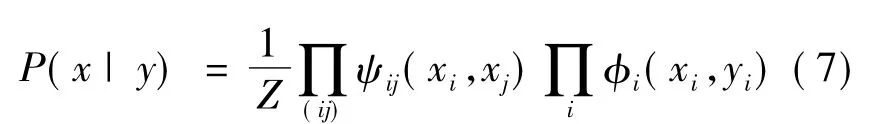
其中:Z为归一化常数。

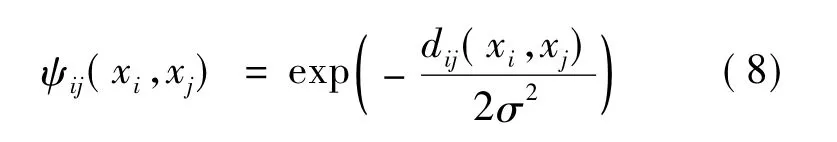
其中:dij(xi，xj)表示候选块xi，xj重叠区域的平方差之和;σ为噪声参数。同样利用相同的马尔科夫网络来说明φi(xi，yi)。由于需要构建数十万个高分辨率与低分辨率图像块对来计算马尔科夫网络，因此计算量大。为了改善这种情况，针对这个样本的恢复，Yang［14］提出了基于in－place样本回归的超分辨率算法，该算法的主要实现可以用图1来表示。

图1 重建模型

图1中:y代表输入低分辨率图像Y上面的小块，y0代表对Y进行高斯滤波之后的低分辨率图像上取得小块，x0同样也是从X0上面提取的图像。学习算法主要是对一阶回归函数▽F进行学习，不需要直接对回归函数F(F是指低分辨率图像块y空间到高分辨率图像块x空间的映射)进行学习，这样得到的结果不仅更加精确，而且效率也有所提高。利用该算法，基本上能够实现实时处理，实现了5倍放大效果的超分辨率图像效果仍较好。

1.2.2 基于稀疏表示的超分辨率图像恢复

Olshausen［15］于1996年首次提出了学习字典的概念，并指出:“当稀疏编码应用于二维图像时，学习到的基与哺乳动物视觉皮层V1区内各种神经元的反应特性类似，并且证明了基于学习的字典比经典的字典表达更精确，更接近人类反应，自适应性较强”。稀疏特性充分考虑了人眼的视觉特性，利用该算法恢复的图像效果较好。Yang［16］提出了一种基于稀疏编码的学习算法，该算法是从外部图像样本直接选取高低分辨率图像块作为高低分辨率字典，之后利用字典求解稀疏系数进行超分辨率图像恢复。该算法的缺陷是高低分辨率图像块之间并没有稀疏关联，而且选择样本时很难选择合适的样本，因此运行时间相对较长。后来Yang［17］又提出了一种稀疏联合来求解高低分辨率字典，它的基本思想是将图像的高分辨率块和低分辨率块的特征进行联合稀疏求解，特征的选择一般选用一阶和二阶因子来提取，这样学习得到目标字典对，使得高低分辨率图像具有相同的稀疏表示。该算法大大提高了运算速度以及重建效果，由于算法仍然采用的是线性求解，因此算法收敛较慢。之后又有研究者对这个字典训练进行改进［18］，改进的算法在选择字典时速度仍然较慢，而字典的选择对于恢复图像的效果至关重要。Zeyde［19］对文献［18］使用了不同的训练方法，从而在算法结构和复杂度上都进行了改进，最终恢复图像的效果有了很大改善。而后，廖秀秀［20］提出了双稀疏字典的超分辨率图像重建算法，这种恢复算法不仅在性能方面有所提升，而且速度也大大加快。

2 后续研究和展望

本文介绍了现有的一些超分辨率图像恢复算法的优缺点。基于插值的恢复算法简单，一般作为初始的高分辨率估计。基于重建约束的超分辨率图像重建一般要考虑多幅具有位移的低分辨率图像进行匹配，融合去求解高分辨率图像，这个过程中配准程度精度对图像是否出现伪边缘影响很大。而且当放大因子达到一定程度时，即使有多幅低分辨率图像仍然不能改变其效果。因此，综合考虑，在目前基于稀疏的超分辨率图像恢复已经能够做出很好的效果且时间代价也不是很大的情况下，基于稀疏的超分辨率图像恢复算法是最具研究前景的。综上所述，目前超分辨率图像恢复方法研究包括:

1)如何让图像的细节更加清晰。当放大因子较大时，仍然能够恢复出和原始图像接近的图片。

2)稀疏联合字典的求解。让求解的稀疏系数更加完备且更加满足人眼视觉特性要求。

3)文献［21］指出，虽然稀疏重建和样本算法都已经达到了较好的效果，但是如果把回归模型考虑到图像恢复中，那么重建质量将会有更大的改进和提升。基于样本的选择和回归模型的结合在文献［14］中已实现了就目前而言相对较好的效果，因此考虑若将稀疏和回归模型结合也许能达到较好的恢复效果。

4)软硬有机结合实现超分辨率图像恢复。考虑将前端的硬件实现并做出改进，使硬件实现时达到一定的效果，再利用恢复算法实现超分辨率，使方法倍数达到更大。

5)图像质量评价。如何找到一个比较符合人眼视觉效果的评判标准对图像的研究有重要意义。

［1］蒲剑，张军平，黄华.超分辨率算法研究综述［J］.山东大学学报:工学版，2009(1).

［2］Tsai R Y，Huang T S.Uniqueness and estimation of three－dimensionalmotion parameters of rigid objects with curved surfaces［J］.Pattern Analysis and Machine Intelligence，IEEE Transactions on，1984(1):13－27.

［3］郭伟伟，章品正.基于迭代反投影的超分辨率图像重建［J］.计算机科学与探索，2009，3(3):321－329.

［4］肖创柏，禹晶，薛毅.一种基于MAP的超分辨率图像重建的快速算法［J］.计算机研究与发展，2009(5): 872－880.

［5］肖杰雄.基于POCS算法的超分辨率图像重建［D］.上海:上海交通大学，2009.

［6］刘琚，乔建苹.基于学习的超分辨率重建技术［J］.智能系统学报，2009，4(3):199－207.

［7］Yang J，Wright J，Huang T，et al.Image super－resolution as sparse representation of raw image patches［C］//Computer Vision and Pattern Recognition，2008.CVPR 2008. IEEE Conference.USA:IEEE，2008:1－8.

［8］邹谋炎.反卷积和信号复原［M］.北京:国防工业出版社，2001.

［9］刘志文，潘晓露，李一民.L1范数的总变分正则化超分辨率图像重建［J］.微处理机，2012，33(3):37－39.

［10］Irani M，Peleg S.Super resolution from image sequences［C］//Pattern Recognition，1990.Proceedings，10th International Conference.USA:IEEE，1990，2:115－120.

［11］JointMAPRegistration and High－Resolution Image Estimation Using a Sequence of Under－sampled Images［Z］.

［12］王学玲.基于POCS算法的序列图像超分辨率复原技术研究［D］.青岛:中国海洋大学，2007.

［13］Freeman WT，Jones T R，Pasztor E C.Example－based super－resolution［J］.Computer Graphics and Applications，IEEE，2002，22(2):56－65.

［14］Yang J，Lin Z，Cohen S.Fast Image Super－Resolution Based on In－Place Example Regression［C］//Computer Vision and Pattern Recognition(CVPR)，2013 IEEE Conference.USA:IEEE，2013:1059－1066.

［15］Olshausen B A.Emergence of simple－cell receptive field properties by learning a sparse code for natural images［J］.Nature，1996，381(6583):607－609.

［16］Yang J，Wright J，Huang T，et al.Image super－resolution as sparse representation of raw image patches［C］//Computer Vision and Pattern Recognition，2008.CVPR 2008. IEEE Conference.USA:IEEE，2008:1－8.

［17］Yang J，Wright J，Huang T S，et al.Image super－resolution via sparse representation［J］.Image Processing，IEEE Transactions on，2010，19(11):2861－2873.

［18］Yang S，Wang M，Chen Y，et al.Single－image super－resolution reconstruction via learned geometric dictionaries and clustered sparse coding［J］.Image Processing，IEEE Transactions，2012，21(9):4016－4028.

［19］Zeyde R，Elad M，Protter M.On single image scale－up using sparse－representations［M］.Curves and Surfaces. USA:Springer Berlin Heidelberg，2012:711－730.

［20］廖秀秀.基于学习的图像超分辨率重建算法研究［D］.广州:华南理工大学，2013.

［21］Kim K I，Kwon Y.Single－image super－resolution using sparse regression and natural image prior［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2010，32(6):1127－1133.

(责任编辑 杨黎丽)

Review of Super-resolution Image Restoration Method

XIANG Hai－yan
(Key Laboratory of Signal and Information Treatment，Chongqing University of Posts and Telecommunications，Chongqing 400065，China)

As the limitation of imaging technology，improving super－resolution from the hardware needs expensive cost，so we consider implementing super－resolution image from the software.Firstly，this paper is a brief introduction of the previous super－resolution restoration technology，and then based on this，this paper puts forward the algorithm research direction and development in the future.

super－resolution;high resolution image;low resolution image，image restoration

TP13

A

1674－8425(2014)09－0072－05

10.3969/j.issn.1674－8425(z).2014.09.016

2014－05－18

国家自然科学基金项目(61275099)，信号与信息处理重庆市市级重点实验室建设项目(CSTC，2009CA2003)，重庆市自然科学基金项目(CSTC，2010BB2398)和重庆市科技攻关计划项目(CSTC，2011AB2008)

向海燕(1990—)，女，重庆万州人，硕士研究生，主要从事图像处理方面的研究。

向海燕.超分辨率图像恢复方法综述［J］.重庆理工大学学报:自然科学版，2014(9):72－76.

format:XIANG Hai－yan.Review of Super－resolution Image Restoration Method［J］.Journal of Chongqing University of Technology:Natural Science，2014(9):72－76.