优化的邻近支持向量机在图像检索中的应用

王华秋，王斌

(重庆理工大学计算机科学与工程学院，重庆 400054)

优化的邻近支持向量机在图像检索中的应用

王华秋，王斌

(重庆理工大学计算机科学与工程学院，重庆 400054)

邻近支持向量机由支持向量机衍生而来，它将支持向量机中二次规划问题的求解转换为线性方程组的求解，从而能在保证一定精度的情况下更加快速地得到分类器。传统的非线性核邻近支持向量机不能很好地解决多范围数据的多分类问题。提出了一种邻近支持向量机的优化方法，并将其应用到图像检索中。它利用高斯函数将图像特征数据映射到0～1之间以提高其差异化水平，并将其放入非线性核中，然后以加权K－means聚类算法选择最优参数，从而提高了非线性核PSVM的分类能力。实验以coral图像库中的4类图片作为图片库，对比了优化前后的检索命中率。实验结果表明:优化后的检索效果优于优化前，说明将优化的邻近支持向量机应用于图像检索是有效的。

优化的邻近支持向量机;图像检索;高斯函数;加权聚类算法

SVM最初于20世纪90年代由Vapnik提出，它能够很好地解决小样本、非线性、高维模式识别问题，在解决“维数灾难”和“过学习”等传统困难问题方面表现相当出色［1－5］。但是SVM需要求解二次规划问题，训练时间较长。Fung和Mangasarian［6］于2001年在支持向量机的基础上提出了邻近支持向量(PSVM)这一概念，将支持向量机中的二次规划问题的求解转换为线性方程组的求解，因此该方法能够在基本不损失精度的情况下提高学习速度。近年来，邻近支持向量机在理论研究和算法实现方面都取得了突破性进展。2005年，庄东和陈英［7］将加权的邻近支持向量机应用于文本分类，提高了PSVM对不平衡数据的处理能力，实验结果证明该方法优于传统的SVM。2006年，Mangasarian和Wild［8］提出通过求解样本矩阵特征值的方法构造分类超平PSVM，有效解决了交叉数据的二分类问题。2008年，张曦、阎威武等［9］将小波去噪核主元分析和邻近支持向量机结合起来用于性能监控和故障诊断，具有较好的监控效果，并提出了核函数及其参数的选择对诊断结果准确性具有较大的影响的结论。2012年，王至超、张化祥等［10］在GEPSVM的基础上提出了最值间距支持向量机(TDMSVM)，通过计算得到2个最优超平面，使超平面满足到本类样例的平均距离最小，同时到另一类样例的平均距离最大，进一步降低了时间复杂度。同年，鲁淑霞等［11］提出了增量密度加权邻近支持向量机，有效控制了邻近支持向量机的稀疏性。

本文以coral图像库中4种类型的图片作为图片库，在提取图片特征时以每张图片的灰度共生矩阵量化出来的4个标量作为特征值，在构造分类器时，每张图片为一类。由于不同类型的图片量化出的特征值所处范围不同，而同类型图片量化出的特征值较为接近，所以在使用统一的非线性核PSVM对这些图片进行分类时往往出现部分类型的图片分类效果较好，而另一部分分类效果差的情况，导致平均检索命中率较低。为解决该问题，本文对PSVM算法进行了优化。首先引入高斯函数将所有图片的特征值映射到0～1内，使特征值差异化分布。结合数据挖掘技术［12］，使用加权K－means聚类算法将指定范围内的参数及其对应的检索命中率进行聚类，并以检索命中率最高的类中心所对应的参数作为最优参数。实验结果表明优化后的邻近支持向量机具有较好的多分类效果。

1 PSVM算法及优化方法

1.1 PSVM算法

PSVM的基本原理是将每个点归类于2个尽可能远的平行平面中最接近的一个。该问题可以归结为

式(1)、(2)中:A∈Rm×n是m个n维的特征矩阵，v为惩罚因子;e为单位列向量;D是m×m的对角矩阵，其对角线上每一行的值对应A中样本所属的类别1或－1，其余元素为0。其解由拉格朗日泛函:

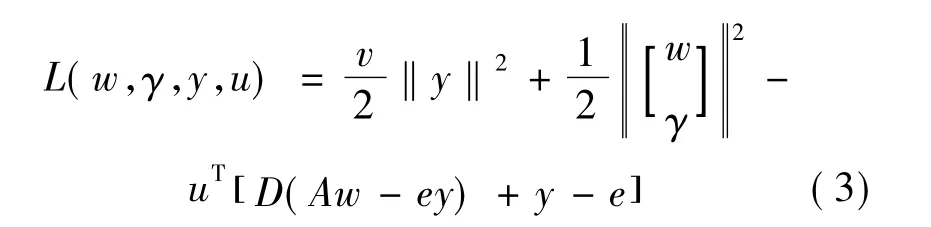
的梯度置零获得。

ui为拉格朗日乘子。对wi，γi，yi，ui求导并令其等于0，可以得到如下4个矩阵式表达式:

由上述4个式子可以得到:

将式(8)～(10)代入式(7)得

将式(11)代入(8)、(9)中得到w，γ。

为了得到非线性分类器，需要把线性分类器中的变量w用其对偶等价w=ATDu替换，并将线性核AAT替换为非线性核k(A，AT)，即

满足约束:

其中:k(A，AT)=(AAT+c)d;c为大于等于0的常数;d原定义为任意正整数，本文将其定义为大于等于0的常数。当c＞0时，该核为非齐次多项式核;当c=0时，为齐次多项式核。

在使用线性分类器对新样本进行分类时，通过wTx－γ的符号来确定该样本属于哪一类。在使用非线性分类器对新样本进行分类时，则通过K(xT，AT)u－γ的符号来确定。在优化的PSVM中特征矩阵A中的值Aij=Gauss(Aij)，其中Gauss(Aij)表示经过高斯函数处理过的特征值。

1.2 PSVM优化方法

1.2.1 最优参数选择

用于训练的特征值是线性不可分的，这里使用非线性核k(A，AT)=(AAT+c)d。在非线性核中包含2个参数c，d，为了得到更高的检索命中率，c，d的确定至关重要。

为了得到较优的参数c和d，首先获取在c∈［0，8］，d∈［0，8］的范围内以0.2为梯度的所有参数下的检索命中率。在候选集合中假设c=ci，d= di所对应的平均检索命中率为Si，然后用加权K－ means聚类算法将三维向量(ci，di，Si)进行聚类，在计算样本之间相似度时使用了加权的欧氏距离，其中赋予Si较高的权值。

这样就得到了高检索命中率所对应参数的集中分布情况，有效地区分了距离较近但命中率差距较大的数据。所有类中心中Si最大的中心所对应的c，d值能在一定程度上代表检索命中率最高的参数，本文称之为最优参数。

1.2.2 特征值预处理

由于使用非线性核的邻近支持向量机不能很好地解决多范围数据的多分类问题，为了减少误差，引入高斯函数:

式(15)中:z为比较中心;σ为函数的宽度参数，其值根据训练特征值及相对差距而定。其中，接近z的特征值在处理过后更接近1，与z差距稍大的更接近于0，σ用来控制相对差距。这样可以将特征值差异化的分布在0～1之间。该方法不仅能起到扩大类与类之间特征值相对差距的作用，而且可规范化数据，将所有特征值映射到0～1，从而提高各类图片的检索命中率。

1.2.3 多分类PSVM

由于二分类的邻近支持向量机往往不能满足图像检索的需求，所以本文引入多分类的邻近支持向量机。

多分类邻近支持向量机同样基于二分类邻近支持向量机，目前常用的有以下两种:

算法11－a－1(one against one)［10］:假设有n类样本，每两类样本构造一个分类器，则该方法需要构造n(n－1)/2种分类器。

算法21－a－r(one against rest)［11］:假设有n类样本，则该方法构造n个PSVM分类器w，第k个分类器在训练时将第k类定为1，其余的定为－1。

考虑到1－a－r法在类别数较多的情况下会出现正负样本不均衡的情况，本文采用1－a－1多分类方法，这样就有2种对新样本分类的决策方法:投票算法、有向无环图算法。

2 图像检索流程设计

图像检索的一般方法是首先将检索范围内的图片特征进行提取并存储，再将检索样本的特征提取出来与检索范围内图片特征进行相似性比对，将相似性最高的图片返回给用户［13］。本文将多分类的邻近支持向量机用于图像检索，不仅要提取图像的特征信息，还要对这些特征进行分类训练，得到若干分类器。当对新样本进行分类决策时，则用每个分类器对新样本进行分类决策，最终根据决策算法得出新样本所属类别［14－15］。具体过程如图1所示。

图1 图像识别流程

3 图像特征获取方法

由于纹理可以通过研究灰度的空间相关特性来描述［16］，因此本文主要以灰度共生矩阵的方法来获取图片的纹理特征。

灰度共生矩阵是对图像上保持距离d的两像素分别具有某灰度的状况进行统计得到的。在得到灰度共生矩阵之前首先要将RGB图转换为灰度图，转换公式如下:

得到灰度值后为了减少计算量，需要将灰度值(0～255)转换为灰度级(0～15)共16级。

假设图片共有M×N个像素点，从某像素点(x，y)开始该像素点的灰度级为i，灰度共生矩阵即统计与其在方向角为θ，距离为d，灰度级为j的像素点同时出现的概率。假设f(xm，xn)为像素点(xm，xn)所对应的灰度级，Count(M)表示M情况出现的次数，由此可将灰度共生矩阵的获取方法概括如下:

为了更直观地反映纹理的特征，可以根据灰度共生矩阵得出一些标量来表征灰度共生矩阵的特征。下面是用到的几种特征值:①能量特征;②对比度;③逆差距;④熵。本文所用的方法是取以上4个特征值分别在θ=0°，θ=45°，θ=90°，θ= 135°的值作为训练集，在对新样本进行分类决策时以新样本4个方向上各特征值的平均值作为特征向量。

4 实验过程及结果

4.1 实验环境

本实验取Coral图片库中的100张恐龙类图片、100张花类图片、100张汽车图片、100张马图片共400张图片作为图片库。实验在WIN7操作系统下进行，使用Visual Studio 2010开发环境进行图像检索系统的设计。实验的硬件环境为:CPU为Intel酷睿2，2.2 GHz双核处理器;内存为2 G。

4.2 实验方法及结果

首先，对图片库中所有图片的特征进行提取，并计算出每张图片所生成的灰度共生矩阵量化出来的4个标量。

然后，从每类图片中随机抽取10张作为图片库进行先验性测试实验，获取各类图片在c∈［0，8］，d∈［0，8］的范围内以0.2为梯度的所有参数对应的检索命中率。所有图片在引入高斯函数前后各参数的平均检索命中率等值线如图2、3所示。

图2 处理前平均检索命中率等值线

图3 处理后平均检索命中率等值线

图2、3中:x轴代表非线性核(AAT+c)d中参数c的值;y轴代表参数d的值。等值线所代表的检索命中率从外向内依次递增。对比图2、3发现，引入高斯函数后的检索命中率较高的参数的范围明显大于引入前。

得到各参数对应的检索命中率后，根据参数值及其对应的检索命中率利用加权的K－means算法进行聚类，以得到最优参数。

各类图片在使用最优参数的PSVM分类后的检索命中率如图4所示。

图4 最优函数下检索命中率(全部样本)

从图4的结果可以看出，引入高斯函数的邻近支持向量机的检索效果要优于引入前。

表1、2给出了引入高斯函数前后最优参数(各表中第1行参数)与最优参数附近参数所对应的检索命中率。对比后发现，最优参数虽然在某一类中的检索命中率不是最高，但具有最高的平均检索命中率，能够较好地满足各类图片的需求。

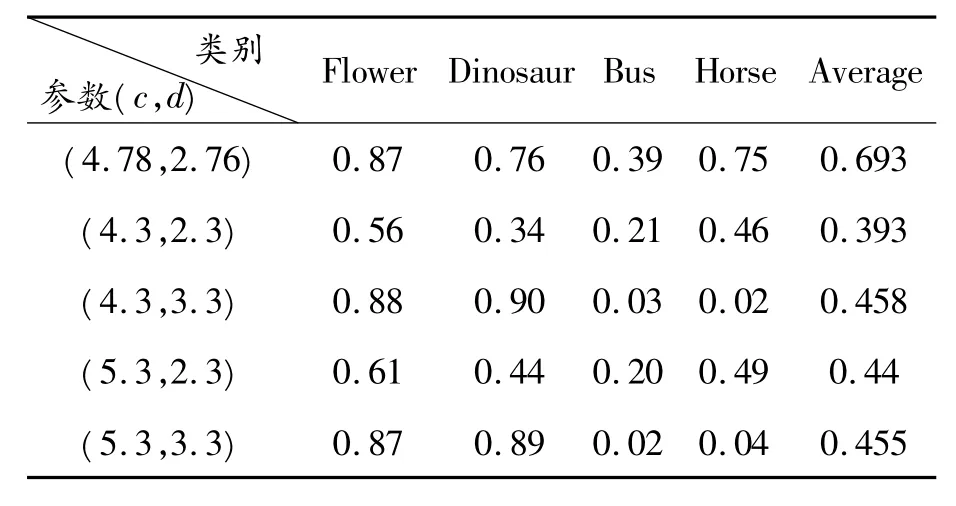
表1 引入高斯函数前检索命中率对比(全部样本)

表2 引入高斯函数后检索命中率对比(全部样本)

在核函数k(A，AT)=(AAT+c)d中，c值对检索命中率的影响较小，d值影响较大，且在引入高斯函数前，选取的参数略大或略小都会较大幅度地降低检索命中率。而在引入高斯函数后，当d略小时，对检索命中率的影响较小。对照图2、3不难发现其原因:引入高斯函数前，检索命中率的坡度在d值增加和减少方向均较大，而在引入高斯函数后，检索命中率的坡度在d值增加方向较大，在减小方向较小。因此，引入高斯函数很好地扩大了非线性核邻近支持向量机较优参数的范围，从而提高了非线性核邻近支持向量机在多分类时的分类效果。

5 结束语

本文对邻近支持向量机进行了一系列的优化并将其应用到图像检索中。实验结果表明优化后的PSVM具有更好的多分类效果，将多分类邻近支持向量机应用于图像检索中是有效可行的。

但该方法仍然存在一定的局限性。例如，该算法在数据量较小时表现较为出色，具有较高的检索命中率，但当数据量变大时，各类图片的检索命中率均出现一定程度的降低，且部分类型图片的检索命中率下降明显。这说明该方法对于图像检索还不具有普适性。所以若将该方法广泛应用于图像检索领域还有很多地方需要改进，如核函数的选取及优化，分类及决策算法的优化、选取更加适合于该方法的特征提取算法等。下一步的研究工作将主要围绕改进PSVM的核函数和获取更适合于该方法的图像特征两个方向展开。

［1］丁世飞，齐丙娟，谭红艳.支持向量机理论与算法研究综述.电子科技大学学报.2011.40(1):2－7.

［2］余珺，郑先斌，张小海.基于多核优选的装备费用支持向量机预测法［J］.四川兵工学报，2011(6):118－119.

［3］万辉.一种基于最小二乘支持向量机的图像增强算法［J］.重庆理工大学学报:自然科学版，2011(6):53－57.

［4］邬啸，魏延，吴瑕.基于混合核函数的支持向量机［J］.重庆理工大学学报:自然科学版，2011(10):66－70.

［5］崔建国，李明，陈希成.基于支持向量机的飞行器健康诊断方法［J］.压电与声光，2009(2):266－269.

［6］Fung G，Mangasarian O L.Proximal Support Vector Machine Classifiers［C］//Knowledge Discovery and Data Mining.New York:Association for Computing Machinery，2001:77－86.

［7］庄东，陈英.基于加权近似支持向量机的文本分类［J］.清华大学学报:自然科学版，2005，45(S1):1787－1790.

［8］Mangasarian O L，Wild EW.Multisurface Proximal Support Vector Machine Classification Via Generalized Eigenvalues［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2006，28:69－74.

［9］张曦，阎威武，赵旭，等.基于小波去噪核主元分析和邻近支持向量机的性能监控和故障诊断［J］.上海交通大学学报，2008，48(2):181－185.

［10］王至超，张化祥.最值支持向量机［J］.计算机科学，2012.39(4):205－209.

［11］鲁淑霞，崔芳芳，忽丽莎.增量密度加权近似支持向量机［J］.计算机科学，2012，39(11):194－197.

［12］Han Jiawei.Data Mining:Concepts and Techniques，Third Edition［M］.Morgan Kaufmann Press，2011.

［13］刘颖，范九伦.基于内容的图像检索技术综述［J］.西安邮电学院学报，2012，17(2):1－8.

［14］Glenn Fung，Olvi LMangasarian.Proximal Support Vector Machine Classifiers，proceeding，KKD，2001(8):77－86.

［15］Hsu CW，Lin C J.A comparison ofmethods for multiclass support vector machines［J］.PPIEEE Transactions on Neural Networks，2002，13(2):415－425.

［16］刘舒，姜琦刚，邵永社，等.应用灰度共生矩阵的纹理特征描述的研究［J］.科学技术与工程，2012.12(33): 8909－8914.

(责任编辑 杨黎丽)

Application of Optim ized Proximal Support Vector Machine in Image Retrieval

WANG Hua－qiu，WANG Bin
(College of Computer Science and Engineering，Chongqing University of Technology，Chongqing 400054，China)

Proximal support vectormachine(PSVM)is derived from support vectormachine(SVM) and converts the quadratic programming problem into linear equations，so that it can ensure the classifiermore quickly under the condition of certain precision.The multi－class classification problem of multi range data can notbe solved well by the original nonlinear kernel PSVM.This paper presents an optimization method for PSVM，and applied the optimized algorithm to image retrieval.The Gauss function is used to image feature datamap to the range of0～1 to enhance their difference level，then the different data is put into nonlinear kernel function，finally weighted K－means clustering algorithmis used to select the optimal parameters of PSVM.Experiments are carried out on 4 types of images from coral image database as the picture library，and the hit rate is compared between the original PSVMand the optimized algorithm.Experiments show that the performance of optimized PSVMis better than original algorithm，and it is effective to use the optimized PSVMinto image retrieval.

optimized proximal support vectormachine;image retrieval;Gauss function;weighted clustering algorithm

TP391

A

1674－8425(2014)09－0066－06

10.3969/j.issn.1674－8425(z).2014.09.015

2014－01－07

教育部科学研究青年基金资助项目(10YJC870037);国家社会科学基金资助项目(14BTQ053)

王华秋(1975—)，男，博士，教授，主要从事数据挖掘和智能控制研究;王斌(1991—)，男，硕士研究生，主要从事数据挖掘研究。

王华秋，王斌.优化的邻近支持向量机在图像检索中的应用［J］.重庆理工大学学报:自然科学版，2014 (9):66－71.

format:WANG Hua－qiu，WANG Bin.Application ofOptimized Proximal Support VectorMachine in Image Retrieval［J］.Journal of Chongqing University of Technology:Natural Science，2014(9):66－71.