一种基于逐点插入Delaunay三角剖分生成Voronoi图的算法

黄清华

一种基于逐点插入Delaunay三角剖分生成Voronoi图的算法

黄清华

采用改进的逐点插入算法生成Voronoi图。该算法在逐点插入的过程中生成凸壳，进而生成Delaunay三角剖分。在生成Voronoi图的实现过程中，通过遍历三角形的边顶点快速识别相关的三角形组，进而生成Voronoi图。试验结果表明，该算法能实现，成功生成Voronoi图。

逐点插入；凸壳；Delaunay三角剖分；Voronoi图

0 引言

Voronoi图与convex hull 和delaunay三角形并称为计算几何的三大支柱，早在1850年Dirichlet及1908年Voronoi在其论文中都讨论过Voronoi图的概念[1]。Voronoi又称泰森多边形或者Dirichlet图。Voronoi图在求解点集或者其他几何对象与距离有关的问题时起着重要作用。从上世纪90年代以来，voronoi图的应用领域在不断扩展，这些领域从几何重构到计算机图形学、图像处理，从路径规划到粒子微观状态分布，几乎涵盖了自然科学领域的大部分学科[2]，足以看出voronoi图的优越性与重要性。所以voronoi的算法实现就显得举足轻重。

最基本的voronoi图是以平面点集P为基础的，点集中的点有序的组成多个凸多边形，这些凸多边形组成了voronoi区域。其重要的一个性质就是点集中的每个点pi对应这样一个区域Vi，区域Vi内的任何点距离pi点比点集内的其他点近，这也决定了voronoi图的独特性。

Voronoi图的对偶图为Delaunay三角剖分。Delaunay三角剖分的生成算法较多且成熟，我们可以通过先生成Delaunay三角剖，在再生成其对偶图来生成Voronoi图。目前 Delaunay三角剖分的生成算法主要有：三角网生长法、分治算法和逐点插入法，其中属逐点插入法应用最广泛，被研究最多。该方法实现简单，易于推广到高维。本文先通过逐点插入法生成Delaunay三角网，再生成Delaunay三角网的对偶图来得到Voronoi图。

1 Delaunay三角剖分算法的概述

Delaunay三角剖分对于数值分析是一项极为重要的与处理技术。Delaunay三角剖分有两个重要的性质：（1）最大化最小角，即最接近于规则化；（2）唯一性，即构成三角网的点集内任意四点不共圆。这两个性质既定义了Delaunay，也确定了应用之时其优越性。Miles 证明了Delaunay三角网是“好的”三角网；Lingas进一步论证了“在一般情况下，Delaunay三角网是最优的。”以上定义及性质是建立Delaunay三角网的算法依据。

Delaunay三角剖分的经典剖分算法可概括为下面两类[3]：

1）增量算法：原理是从一个基本三角形开始，每次增加一个点，重新生成三角网并保证得到的当前三角形是局部优化的三角形。

2）局部变换法：原理为先构造非优化的三角网，然后对两个共边三角形形成的凸四边形迭代换边优化。

迄今为止Delaunay剖分的生成算法，主要有分治算法、逐步插入法、三角网生长法等。比较三种算法：分治算法高效，但实现算法复杂；三角网生长算法效率较低；逐点插入法实现简单,但它的时间复杂度差。时间复杂度缺陷可通过提高硬件水平来弥补。所以综合考量，本文用逐点插入法来生成Delaunay剖分。逐点插入法的代表算法为Lawson算法，由Lawson于1977年提出。逐点插入法的基本步骤为：（1）生成点集坐标数据；（2）生成包围点集的边界即凸壳；（3）综合边界和内部点集生成三角网。

2 Delaunay三角剖分的生成

Voronoi剖分的关键在于生成Delaunay网格。Delaunay剖分的关键技术为：快速创建包含点集的凸壳；插入新点后快速生成新的Delaunay网。逐点插入法是在点集内点大于等于3的情况下每插入一点就生成新的Delaunay，也意味着要生成新的凸壳。

2.1 初始设置

凸壳顶点链表：ConvexHull List；凸壳顶点数组：Vertex Array；剖分后三角形链表：Del-Tri List；三角形顶点链表：Tri-Points List 。

2.2 建立凸壳

凸壳建立有许多经典算法，如分治法、卷包裹法、格雷厄姆扫描法和增量法等[4-5]。卷包裹法和格雷厄姆扫描法等需要对点集进行排序，而增连法则不需要预先排序。本文来用增量递推算法，不需要排序。凸壳CH（S）具体建立步骤如下：

步骤1 初始化凸壳顶点链表ConvexHull List。插入的点数目为3时，取这三点p1，p2，p3围成的三角形为初始凸壳CH(3)（{ p1，p2，p3}）3点放入链表。如图1所示：

图1 初始凸壳CH（3）

图2 凸壳CH（16）

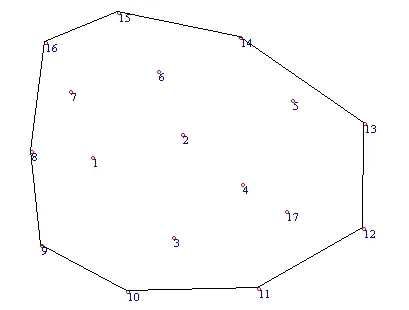
图3 凸壳CH（17）（P17CH（16））

图4 凸壳CH（18）（P18CH（17））

可以直观观察上述两种情况。图2为插入16点时生成的凸壳；图3为插入第17点时生成的凸壳，对应第一种情况；图4为插入第18点时生成的凸壳，对应第二种情况。

(1)找正切点算法：

Then pi在右侧

Else pi在左侧

步骤3链表ConvexHull List即为凸壳点集内的点。

2.3 Delaunay 三角剖分生成[6]

Delaunay三角剖分生成步骤如下：

步骤1 复制链表ConvexHull内数据入数组Vertex，对凸壳构建三角网。从第一点开始依次取点构成构成三角形，在构成三角形之前判断该三角形外接圆中是否包含其他凸壳顶点。包含则重新选点构网，不包含则将三角形加入到链表Del_Tri List。

步骤2 逐点加入修改三角网。插入新点加入三角形顶点链表Tri_Points，定位插入点影响的所有三角形，即点在其外接圆内的三角形。删除受影响三角形的三边，链表Del_Tri内表尾三角形前移插入受影响三角形处。并在受影响区域重新构网。新生成的三角形加入Del_Tri List。

步骤3 重复步骤2，可得要求数目点集的Delaunay三角网。链表Tri_Points内为三角剖顶点，三角形链表Del_TriList即为所求Delaunay三角剖分。

3 Voronoi剖分的生成

Voronoi图与Delaunay三角剖分互为对偶图，本文中用已生成的Delaunay三角剖分生成Voronoi剖分的关键技术在于快速遍历每个点的目标三角形的边。在生成Delaunay三角剖分的过程中生成的凸壳顶点为半封闭边界点，不参与Vonoroi剖分的生成。

链表设置：Voronoi点链表：Vor_Points List；三角形边链表：Tri_Edge List；边终点数组：End_Points Array；

步骤1 在Delaunay三角剖分生成的过程中得到凸壳的顶点链表ConvexHull和三角形的顶点链表Tri_Points。从Tri_Points List中去除ConvexHull中的顶点，将剩余点有序加入新的链表Vor_Points List。

步骤2 在Delaunay三角剖分的基础上，依次遍历每个三角形的3条边，加入链表Tri_Edge。在遍历的过程中，如出现重复的边则不再重复加入。

步骤3遍历链表Vor_Points内的点。对每一点遍历该点相关的边链表Tri_Edge，可得相关的边的另一点，即终点End_Points，结合Tri_Points内点的坐标,可以得到End_Points内的点坐标。

步骤4 将End_Points内点逆时针排序，则同时也对点相关的三角形进行了排序。计算上述有序三角形的外接圆圆心。

步骤5 逆时针连接外接圆圆心，可得Voronoi图。遍历所有点后，可得整体Voronoi图。

4 实现结果与结论

为检验本算法，采用VS2005编译环境、C#语言编程实现了增量算法生成凸壳、逐点插入Delaunay三角剖分，最后生成了Voronoi图。计算机配置为Intel CPU 3.2GHz、4G内存，在逐点插入的过程中生成的凸壳，如图2至图4所示。如图5和6所示：

图5 23点Delaunay三角网

图6 24点Delaunay三角网

是逐点插入过程中生成Delaunay三角剖分。最后生成的Voronoi图如图7所示：

图7 Voronoi图

采用逐点插入算法生成Delaunay三角剖分间接生成Voronoi图。在生成Voronoi图时，通过遍历三角形的边顶点快速识别相关的三角形组，进而生成Voronoi图。结果显示，算法实现很好，成功生成Voronoi图。

[1] AURENHAMMER F. Voronoi diagrams: A survey of a fundamental geometric data structure [ J ]. ACM Computing Surveys, 1991, 23(3) : 345 - 405.

[2] [2]刘金义,刘爽. Voronoi图应用综述[ J ]. 工程图学学报, 2004, 25(2): 125 - 132.

[3] [3]吴莉莉.Delaunay 三角剖分的几种算法综述[J].科技信息，2011,28:119-120

[4] [4]樊广佺，王小牛，杨炳儒.平面点集凸壳的一种近似算法[J].计算机工程与应用2007,43（12）：40-41.

[5] [5]周培德. 计算几何:算法设计与分析[M ]. 3版. 北京:清华大学出版社, 2008.

[6] [6]李水乡，陈斌，赵亮.快速Delaunay逐点插入网格生成算法[J].北京大学学报（自然科学版），2006,03:1-4

A Voronoi Generation Algorithm Based on Point Insertion Algorithm of Delaunay Triangulation

Huang Qinghua
(School of Communication and Engineering, Fudan University, Shanghai 200433, China)

An improved Voronoi generation algorithm based on point insertion algorithm of Delaunay triangulation is presented in this paper. The algorithm generates the convex hull in the process of inserting point by point and then generates Delaunay triangulation. In the process of generating the Voronoi diagram, the algorithm identifies related triangles rapidly by traversing the edge vertices. The experimental results show that the algorithm generates Voronoi diagram successfully.

Point Insertion; Convex Hull; Delaunay Triangulation; Voronoi Diagram

TP391. 41

A

1007-757X(2014)06-0043-03

2014.04.18)

黄清华（1989-），女，复旦大学，硕士研究生，研究方向：计算电磁学，上海，200433