加油机器人操作臂的设计及运动学研究

文/祝 冉 李著信 苏 毅

随着我国国民经济的飞速发展，机动车辆的数量不断增多，许多加油站正变得不堪重负，为提高加油站的工作效率，减少污染，节省人才成本，未来将更多地使用加油机器人来完成加油工作。加油机器人由一个可移动平台和一个操作臂组成。可移动平台负责将整个机器人运送到需要加油的机动车位置，而操作臂则将加油枪准确地插入机动车油箱口，完成加油工作。可见，操作臂在整个系统中起着核心决定性作用。因此，本文主要针对操作臂进行研究。

1.操作臂的结构设计

操作臂是加油机器人的执行机构，要求能够在工作空间内灵活地到达任意位置。根据实际情况，设计四自由度的操作臂如图1所示。

该操作臂由基座1、大臂2、小臂3、手部4共四个部分以及基座关节、肩关节、肘关节、腕关节共四个关节组成。整个结构为空间关节型，四个关节均是转动关节。其中，基座关节实现整个操作臂绕基座轴线的转动；肩关节和肘关节带动大臂、小臂一起作俯仰运动；作为末端执行器的加油枪固结在手部上，且加油枪的轴线与手部轴线重合，腕关节不需作摇摆运动和绕自轴的旋转运动，只作俯仰运动。由以上四个关节即可确定加油枪相对于基座的位置与姿态。

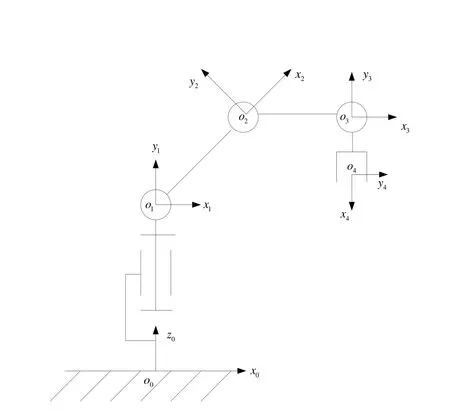
图1 加油机器人操作臂结构简图及D-H坐标系

2.操作臂运动学模型的建立

Denavit和Hartenberg在1995年提出了一种对机器人进行建模的通用方法，即D-H表示法。它的核心思想是：在机器人的每个杆件上都固定一个坐标系，然后用4*4的齐次变换矩阵来表示机器人相邻两杆件之间的位姿关系，再通过依次变换，最终推导出机器人手部相对基座坐标系的位姿矩阵。

若用齐次坐标变换矩阵（位姿矩阵）M表示机器人手部在空间相对基座坐标系的位置和姿态，并将机器人中n个活动关节抽象为关节变量 (i=1,2,…,n)，则机器人手部的位姿矩阵与关节变量之间有一定的函数，即

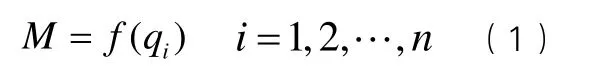
2.1 机器人运动学正问题

在式（1）中，若已知机器人各个关节变量qi，求机器人手部相对于基座坐标系的位姿M，则称为机器人运动学正问题。

在图1中建立杆件标准D-H坐标系，其D-H参数如表1所示。

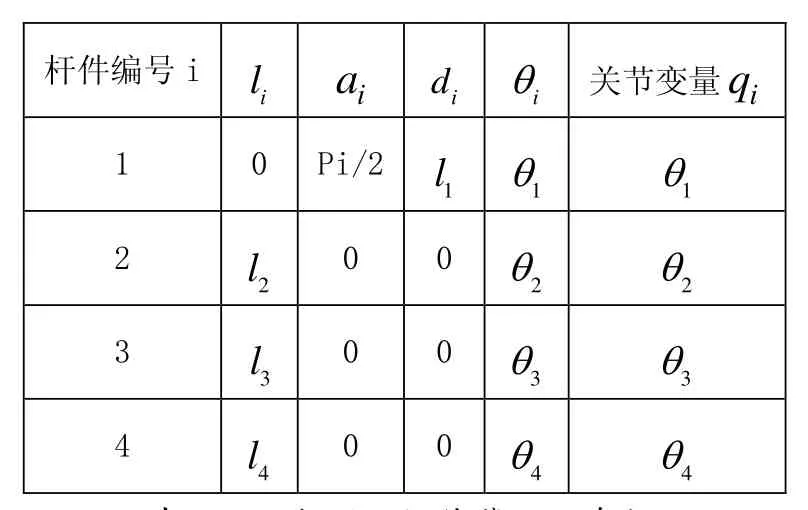
表1 加油机器人操作臂D-H参数

在每个杆件上都固定一个直角坐标系，且固定于每个杆件的上端（编号大的）关节处，杆件的编号从基座开始，基座为0号杆件，与其相连接的杆件为1号，其余依次为2,3,…,n号杆件，杆件上固结的坐标系与该杆件同号。机器人的关节编号从第一个关节开始，依次计为1,2,3,…,n。用齐次变换矩阵01M表示第1杆系相对于基座坐标系的位姿，12M表示第2杆系相对于第1杆系的位姿，表示第i杆系相对第i-1杆系的位姿，其余依次类推。

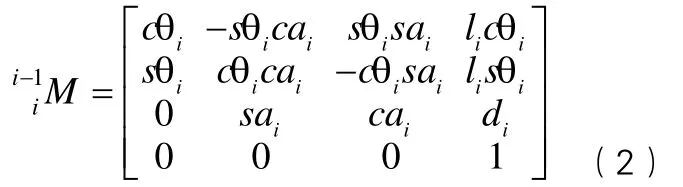
则机器人手部相对于基座坐标系的变换矩阵为：

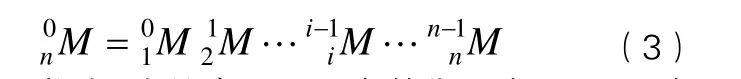
将表1中给出的D-H参数代入式（2）、式（3）中，可得加油机器人操作臂的正运动学方程

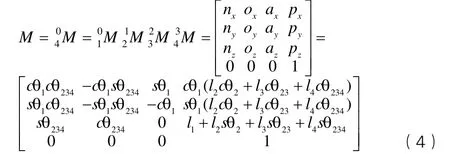
给定一组关节变量和参数的值，我们就可以利用式（4）计算出位姿矩阵中每个元素的值，得到一个唯一的位姿矩阵M。

2.2 机器人运动学逆问题

在式（1）中，若已知机器人手部相对于基座坐标系的位姿M，求机器人各个关节变量qi的值，则称为机器人运动学逆问题。

其求解方法是利用机器人运动学方程两端矩阵元素应相等的原理得到一组多变量的三角函数方程，通过求解这组方程来确定机器人各个关节变量的值。逆问题的解不是唯一的，当存在多个解时，应根据实际关节运动范围的限制舍去一些解，在余下的有效解中，根据最接近原则，选取出一个最接近于当前机器人操作臂的逆解。

根据式（2）中矩阵两边元素相等，可建立带有关节变量的6个函数方程（5—10）：

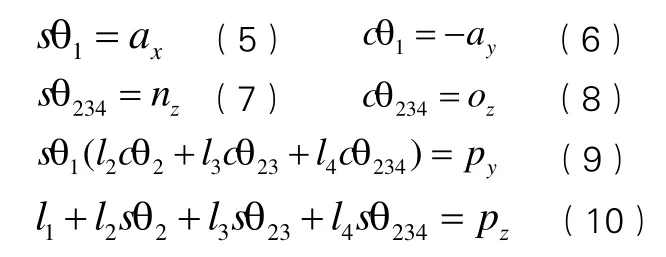
由（5）（6）两式可得

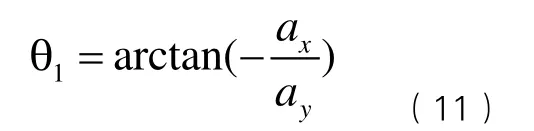
又由（7）（8）两式可得

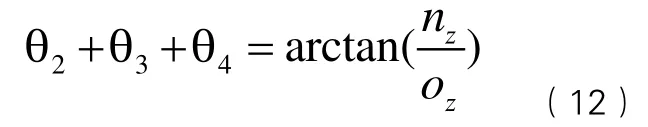
联立（9）（10）两式，先移项，再将其两边平方相加，即可解出

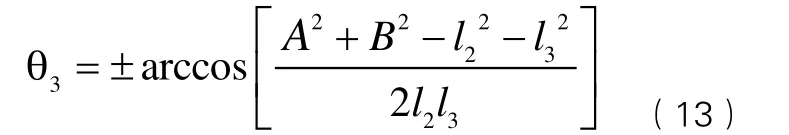
将（9）（10）两式中的23cθ ，23sθ 展开，可得方程组

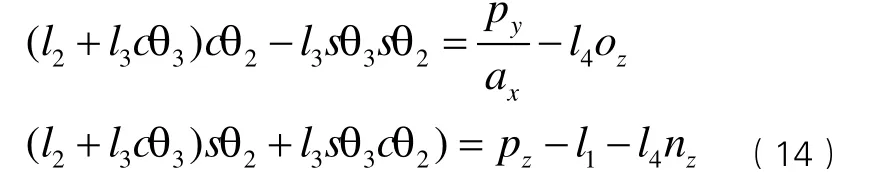
由于已知 c θ23，因此也可求得，即可将

cθ23，sθ23视为已知数代入方程组（14）中，可得

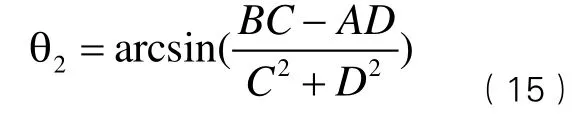
根据式（12），可得

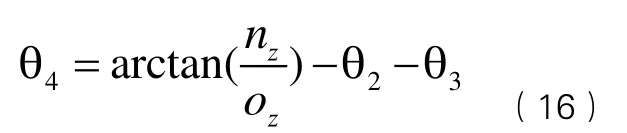
综上可知，式(11) 、(13)、(15)、(16)即为逆运动学方程。

3.正、逆运动学方程的验证

通过利用MATLAB软件中的机器人工具箱Robotics Toolbox来作计算，以此来验证我们所建立的加油机器人操作臂正、逆运动学方程的正确性。

3.1 正运动学方程的验证

根据实际工作情况和操作臂的工作空间限制，对各关节参数与变量赋予初值：

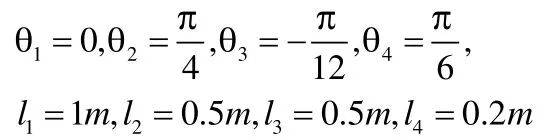
代入（4）中，得出位姿矩阵中各元素的值。

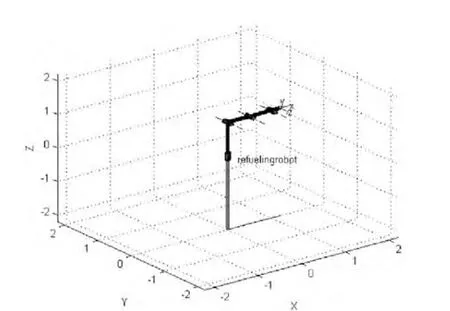
图2 三维建模图

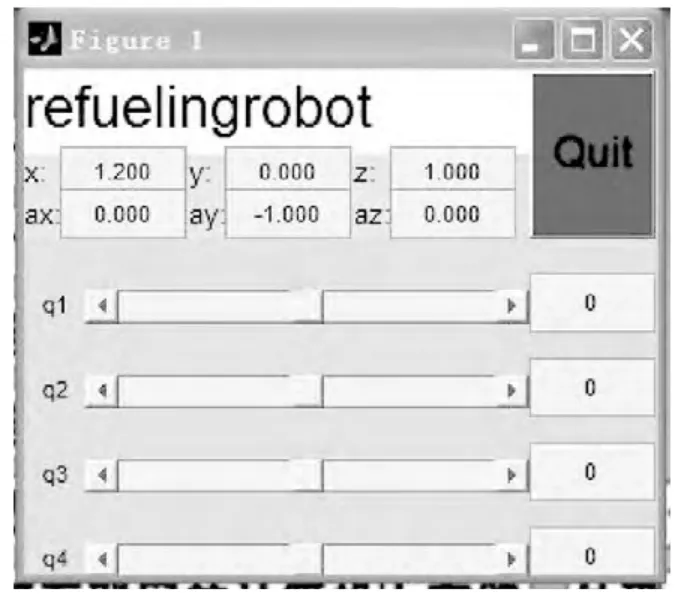
图3 滑动控制框

可知，矩阵F中各元素的值与式（17）中各元素的值是相等的，所以加油机器人操作臂的正运动学方程是正确的。

3.2 逆运动学方程的验证

现假设已知位姿矩阵F，我们将F中各元素的值代入式（11）、（13）、（15）、（16）中，可得两个解

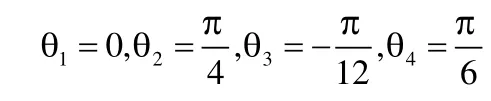
或

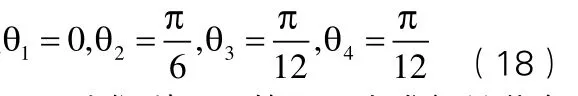
然后，我们利用函数ikine来求解关节变量

>> qr=ikine(r,F)

qr=-0.0000 0.5236 0.2618 0.2618

即qr = 0 pi/6 pi/12 pi/12

可知，我们利用MATLAB求出的解是逆方程式求出的两个解（式18）的其中之一，所以加油机器人操作臂的逆运动学方程是正确的。

4.结束语

本文针对加油机器人操作臂进行了结构与参数设计，采用标准D-H坐标系建立了运动学方程，利用两端矩阵元素应相等的原理求出逆解，然后以MATLAB中的Robotics Toolbox为工具，并编写建模与计算程序，验证了正、逆运动学方程，证明了所建立的加油机器人操作臂模型是正确的，为下一步动力学分析与轨迹规划奠定了基础。

[1] 朱世强，王宣银. 机器人技术及其应用[M]. 杭州：浙江大学出版社，2001.

[2] 蔡自兴. 机器人学[M]. 北京：清华大学出版社，2000.

[3] 马香海. 机器人机构学[M]．北京：机械工业出版社，1991.

[4] 景振毅，张泽兵，董霖．MATLAB 7.0实用宝典[M]．北京：中国铁道出版社，2009.

[5] 罗家佳，胡国清．基于Matlab的机器人运动仿真研究[J]．厦门大学学报，自然科技版，2005，44(5)：640～644.

[6] J．J．Craig．Introduction to Robotics：Mechanics and Control[M]．3rd ed．New York：Prentice Hal1，2005．

[7] P. Corke．A Robotics Toolbox for MATLAB[J]．IEEE Robotics and automation Magazine，1996，3(1)：24～32．8.

[8] Tan J D，xiN Hybird force/position Control of mobile mampulators．IFAC，2002．