一种非单调L－BFGS方法及其全局收敛性

邹 舒，周群艳

(江苏理工学院 数理学院，江苏 常州 213001)

0 引言

考虑非线性无约束最优化问题

其中f:Rn→R二次连续可微。

拟牛顿法是求解问题(1)的最有效的方法之一。线搜索拟牛顿法最基本的迭代格式[1]是xk+1=xkαkHkgk，k=0，1，2，…。其中 x0给定，αk是由某种线搜索方法计算得到的步长，gk= ▽f(xk)，Hk∈Rn×n是当前迭代点xk处Hesse阵的逆的近似，满足拟牛顿方程Hk+1yk=sk，其中sk=xk+1－xk，yk=gk+1－gk。通常Hk可借助拟牛顿公式校正得到，比如BFGS公式，其中在过去的几十年中，BFGS拟牛顿算法被广泛应用于非线性最优化，其全局与局部收敛性得到了论证。然而，当n较大时，不可能存储以及校正一个n阶的方阵。对于大规模无约束优化问题，有限内存BFGS(L－BFGS)算法更受青睐。

L－BFGS法是在BFGS法的基础上改变得到的。若在第k步，已经存储了m对最近的(si，yi)，i=k－m+1，L，K。选取Hesse阵▽2f(xk+1)的初始逆矩阵的近似H(0)k+1，用BFGS公式校正H(0)k+1^m=min(m，k)次，就得到▽2f(xk+1)的逆矩阵的近似Hk+1。故L－BFGS法中的Hk+1为[2]:

L－BFGS法最主要的优点是不需要明显地存储n阶方阵Hk，只需存储第k步的向量Hkgk，这可以通过文献[1]中提出的双循环算法计算得到。双循环算法代价低，且H(0)k的计算独立于其它的计算过程。

尽管有限内存法被认为非常有效，但是对于一些坏条件问题，可能速度非常慢。然而，可通过对初始Hesse阵的逆矩阵使用预条件的方式大大改进有限内存法的效率。本文尝试着从另一个角度来改进LBFGS算法。我们注意到当今比较流行的非单调技术多数应用在牛顿类方法、共轭梯度法或信赖域算法，对有限内存类算法使用非单调技术的研究较少。

1 算法

通常的L－BFGS法使用如下的Wolfe－Powell准则确定步长因子中0＜σ1＜σ2＜1。为提高L－BFGS算法的效率，Yuan，Wei和Wu在文献[3]中提出了一种采用Grippo[4]的非单调技术的L－BFGS法，要求步长因子αk满足，其中，H为一非负整数。但这种方法只要求下一个迭代点处的函数值小于前面几步迭代过程中函数的最大值，一定程度上忽视了当前迭代点处的函数值，影响了算法的效率。为了克服这一缺点，本文引进文献[5]中的非单调策略，记Rk=ηkfl(k)+(1－ηk)fk，给出新的非单调 Wolfe准则

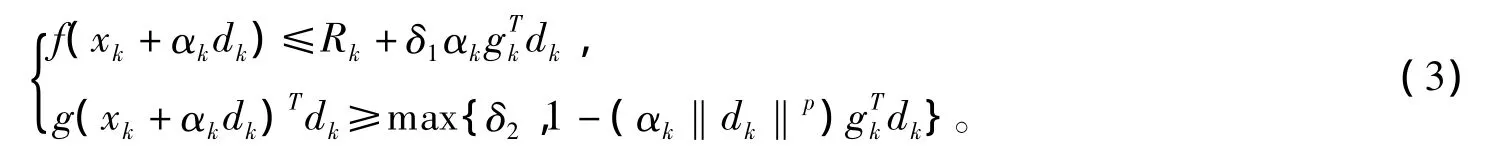
下面给出新的非单调L－BFGS算法。

算法1:

步0:给定 x0∈Rn，0 ＜ δ1，δ2＜1，0 ＜ ε ＜1=I，置 k=0;

步1:计算 gk，若‖gk‖≤εmax{1，‖xk‖}，停止计算，否则转步 2;

步2:计算 dk= －Hkgk，xk+1=xk+αkdk，其中 αk满足准则(3);

为了便于进行收敛性分析，记Hk的逆为Bk，则算法1的步2和步3等价于

步2’:解 Bkdk= －gk得 dk，令 xk+1=xk+ αkdk，其中 αk满足准则(3)。

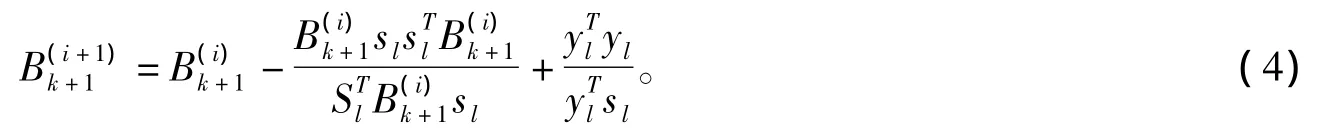
2 收敛性分析

假设1(1)水平集Ω={x|f(x)≤f(x0)}有界。(2)函数f(x)在Ω上二次连续可微。(3)f(x)一致凸，即存在两个正数N1和N2使得对任何z∈Rn和x∈Ω有N1‖z‖2≤zTG(x)z≤N2‖z‖2。

显然在假设条件下，存在M*＞0使得‖G(x)‖≤M*，x∈Ω。另外，假设1(2)表明存在一个常数L≥0满足‖g(x)－g(y)‖≤L‖x－y‖，x，y∈Ω。

以下的定理1、定理2和定理3在文献[3]中已经证明，这里仅加以叙述。

定理2 若Bk

定理3 若假设1(3)成立，则存在b0＞0使得，其中

定理4 若假设1成立，序列{xk}为算法产生的序列，则{f(xI(k))}收敛。

证:由Rk和 f(xI(k))的定义以及线搜索准则(3)得 Rk=ηkf(xI(k))+(1－ηk)fk≤ηkf(xi(k))+max{f(xI(k))，Rk}≤f(xI(k))，故{fI(k)}单调下降，又 fk+1≤fI(k+1)≤fI(k)≤f0，即序列{xk}含于 Ω 中，所以{f(xI(k))}收敛。

定理5 如果

历史是在高中阶段学习的一门重要的文科课程，历史学习能够帮助学生正确认识人类社会经济与政治等方面的发展与演进，对学生综合素质的发展有着积极的影响。因此教师在组织教学活动的过程中需要重视对高中生历史核心素养的培养，为学生培养历史核心素养，能够帮助学生站在历史的角度认识问题、分析问题，对学生今后的学习与发展有着积极作用。在进行历史核心素养培养的过程中，不仅需要对课本的基础知识和内容进行学习，还需要站在历史发展的角度进行归纳与总结，将高中历史课堂赋予浓厚的人文与历史气息。

其中 tk≥0，则

证明 由式(5)和定理4得f(xk+1)≤Rk－tk≤f(xI(k))－tk，f(xk+2)≤Rk+1－tk+1≤f(xI(k+1))－tk+1≤由此可得

分别选取 k=0，H+1，…，(n－1)(H+1)，可得，将这 n 个不等式相加

又由xI(nH+n)∈Ω及序列{f(xI(k))}单调下降得，于是

下面的定理6和定理7见文献[3，6]。

定理6 如果非负数序列{mk}满足，…，则 lim supkmk＞0。

定理7 若假设成立，序列{xk}为算法产生的点列。如果，则存在 ε ＞0，使得对任

定理8 若假设成立，序列{xk}为算法产生的点列，则

证明 由定理3和线搜索准则(3)得 fk+1≤Rk≤f(xI(k))－ε1‖sk‖ηk(xI(k))≤f(xI(k))－。令由定理 5 得

因此

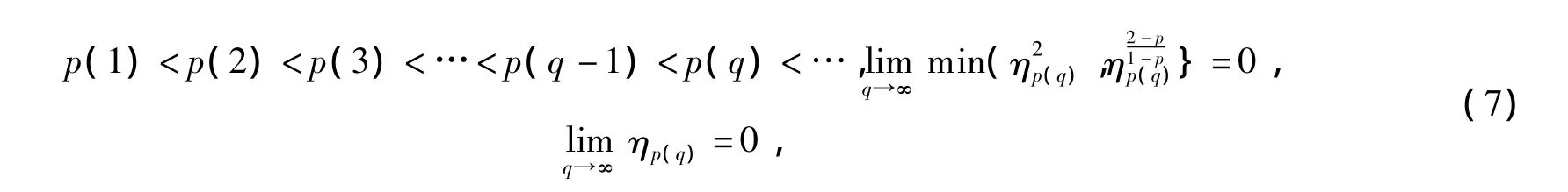
因为xk∈Ω，并且Ω有界，所以可假设存在一个常数b3＞0使‖gk‖≤b3。故有

[1]袁亚湘，孙文瑜.最优化理论与方法[M].北京:科学出版社，1997.

[2]Conn A R，Gould N IM，Toint Ph L.Trust－ Region Methods[M].Philadelphia，PA:MPS/SIAM Series on Optimization，Society for Industrial and Applied Mathematics(SIAM)，Mathematical Programming Society(MPS)，Philadelphia，PA，2000.

[3]YUAN Gong －liu，WEIZeng － xin，Wu Yan － liu.Modified limited memory BFGSmethod with nonmonotone line search for unconstrained optimization[J].J.Korean Math.Soc.，2010，47:767 －788.

[4]Grippo L，Lamparillo F，Lucidi S.A nonmonotone line search technique for New ton’smethod[J].SIAM J.Numer.Anal.，1986，23:707 －716.

[5]Ahookhosh M，Amini K.An efficientnonmonotone trust－ regionmethod for unconstrained optimization[J].Numer.Algor.，2012，59:523 －540.

[6]HAN Ji－ ye，LIU Guang － hui.Global convergence analysis of a new nonmonotone BFGS algorithm on convex objective functions[J].Computational optimization and applications，1997，7:277 －289.