利用逆向思维,设辅助函数解决有关中值问题
2014-07-01邱香兰
邱香兰
(萍乡学院,江西 萍乡 337000)
运用数学知识解决实际问题时有两种思维方式,正向思维和逆向思维。逆向思维法是指为实现某一创新或解决某一因常规思路难以解决的问题,而采取反向思维寻求解决问题的方法。设辅助函数是由题设条件及所给的数量关系,构造一种新的函数、使问题在新的关系下实现转化从而获得解决的方法。利用逆向思维,设辅助函数解决有关的中值问题,就是由问题结论及题中所给的数量关系,构造一种新的函数、使中值问题在新的关系下实现转化从而获得解决的方法。
1 解决中值问题的主要理论知识
1.1 罗尔定理
如果函数f(x)在闭区间[a,b]上连续,在开区间(a,b)内可导,在区间端点处的函数值相等,即f(a)=f(b),那么在(a,b)内至少有一点ξ(a<ξ<b),使得f'(ξ)=0
1.2 拉格朗日中值定理
如果函数f(x)在闭区间[a,b]上连续,在开区间(a,b)内可导,那么在(a,b)内至少有一点ξ(a<ξ<b),使等式f(b)-f(a)=f'(ξ)(a-b)成立。
1.3 柯西中值定理
如果函数f(x)及F(x)在闭区间[a,b]上连续,在开区间(a,b)内可导,对任一x∈(a,b),F'(x)≠0,那么在(a,b)内至少有一点ξ(a<ξ<b),使等式成立。
1.4 泰勒中值定理
如果函数f(x)在含有x0的某个开区间(a,b)内具有直到(n+1)阶的导数,则对任一x∈(a,b)有:

这里ξ是x0与x之间的某个值。
2 中值问题的解题方法及举例说明
考察分析罗尔定理、拉格朗日中值定理、柯西中值定理的结论以及泰勒中值定理的条件可以得出下面有关中值问题的一般解题方法:
2.1 证明含一个中值的等式或根的存在
多用罗尔定理,可用原函数法找辅助函数。即若命题为证明在区间(a,b)内存在ξ使R(ξ,f(ξ),f'(ξ))=0,可考虑由R(ξ,f(ξ),f'(ξ))得出R(x,f(x),f'(x)),由此用原函数法找辅助函数F(x),使其在某区间上满足罗尔定理,且F'(ξ)=R(ξ,f(ξ),f'(ξ))=0,或F'(ξ)=G(ξ)R(ξ,f(ξ),f'(ξ))=0,且G(ξ)≠0.
例1:设f(x)在[0,1]上连续,在(0,1)内可导,且f(1)=0.证明至少存在一点ξ∈(0,1),使
证:问题转化为ξf'(ξ)+2f(ξ)=0,

设辅助函数 F(x)=x2f(x),显然F(x)在[0,1]上连续,在(0,1)内可导,且f(0)=f(1)=0,即满足罗尔定理条件,故至少存在一点ξ∈(0,1),使
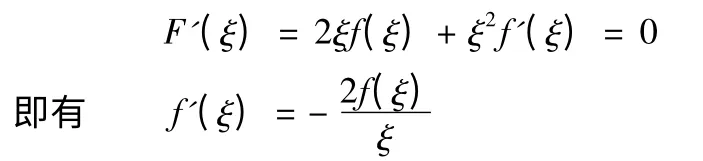
例2:设实数a0,a1,a2,…,an,满足下述不等式

证明方程a0+a1x+…+anxn=0,在(0,1)内至少有一个实根.
证:令F'(x)=a0+a1x+…+anxn,则可设

显然,F(x)在[0,1]上连续,在(0,1)内可导,且f(0)=f(1)=0,即满足罗尔定理条件,故至少存在一点ξ∈(0,1),
使 F'(ξ)=0.
即a0+a1x+…+anxn=0在(0,1)内至少有一个实根.
2.2 若结论中涉及含中值的两个不同函数,可考虑用柯西中值定理
例3:设f(x)在闭区间[a,b]上连续,在开区间(a,b)内可导,且0<a<b.试证存在ξ,η∈(a,b),使:

因f(x)在[a,b]上满足拉格朗日中值定理的条件,故有

又f(x)及x2在[a,b]上满足柯西中值定理的条件,故有

2.3 若结论中含两个或两个以上的中值,必须多次应用拉格朗日中值定理
例4:已知函数f(x)在[0,1]上连续,在(0,1)内可导,且f(0)=0,f(1)=1,证明:
(1)存在ξ∈(0,1)使得f(ξ)=1-ξ;
(2)存在两个不同的点,η,ξ∈(0,1),使得f'(η)f'(ξ)=1.
证:(1)令g(x)=f(x)+x-1,则g(x)在[0,1]上连续,且g(0)=-1<0,g(1)=1>0,故存在ξ∈(0,1),使g(ξ)=f(ξ)+ξ-1=0,即 f(ξ)=1-ξ.
(2)根据拉格朗日中值定理,存在η∈(0,ξ)⊂(0,1),ζ∈(ξ,1)⊂(0,1),使

2.4 若已知条件中含高阶导数,多考虑用泰勒公式
特别是证明与函数的导数在某一点取值有关的不等式时,往往考虑函数在某点的泰勒公式。

根据泰勒中值定理,当x≠0时,有

[1]同济大学数学系.高等数学(上册)[M].第6版.北京:高等教育出版社,2007.128-144.
[2]徐兵,肖马成,周概容.2009年考研数学历年真题解析与应试对策[M].北京:高等教育出版社,2008.38.
