有效解决电磁感应中的焦耳热问题
2014-06-29丁英伟
丁英伟
(徐州市第三十五中学 江苏 徐州 2210 03 )
电磁感应试题是考查学生对基础知识、基本技能的掌握程度和运用所学知识分析、解决问题能力的常见题,也是高考试题的命题热点.特别是焦耳热问题,这些题目既注重基础,又不乏灵活的变化,或与闭合电路欧姆定律、交变电流结合在一起,或与功、能量守恒定律相结合,考查了学生分析综合问题的能力.焦耳热问题也是学生普遍感到学习困难的地方.如何更有效地解决这类问题呢?下面陈述几种方法供读者参考.
1 根据焦耳定律Q=I2 R t求解
【例1】如图1(a)所示,一个电阻值为R,匝数为n的圆形金属线圈与阻值为2R的电阻R1连接成闭合回路,线圈的半径为r1,在线圈中半径为r2的圆形区域内存在垂直于线圈平面向里的匀强磁场,磁感应强度B随时间t变化的关系图线如图1(b)所示,图线与横、纵轴的截距分别为t0和B0,导线的电阻不计,求:
(1)0~t1时间内通过电阻R1上的电流;
(2)0~t1时间内通过电阻R1上产生的热量.
解析:(1)由图像可知,0~t1时间内

而
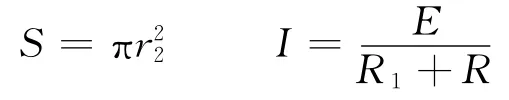
联立以上各式解得

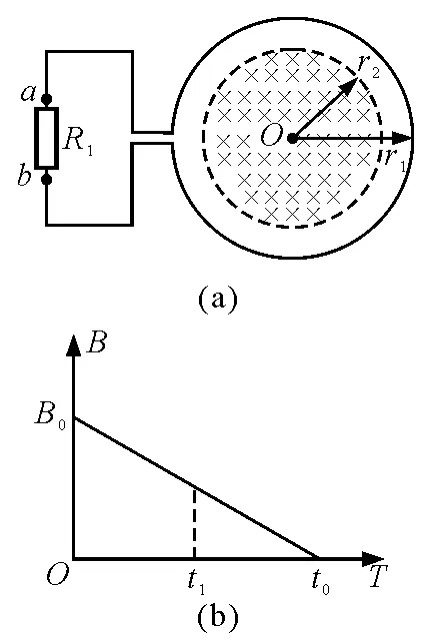
图1
(2)通过电阻R1上产生的热量

点评:此题涉及了感生电动势,由于磁场均匀变化产生稳定不变的感应电流,可以直接根据焦耳定律Q=I2R t求解,还要注意磁通量的有效面积.
(1)棒到达最低点时回路中产生的电流;
(2)若棒在拉力作用下,从c d开始以速度v0向右沿轨道做匀速圆周运动,则在棒到达a b的过程中回路中产生的焦耳热.

图2
解析:(1)到达最低点时
E=Blv
由向心力公式得

联立以上各式解得

(2)棒在水平方向的分速度
vx=v0cosθ
式中θ为速度与水平方向的夹角,即棒转过的圆心角
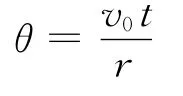
所以瞬时电动势为

因此,棒切割磁力线产生的是正弦式交流电,且有效值为

则

点评:此题涉及动生电动势,公式E=Blv中速度方向必须与磁场方向垂直,棒在匀速转动过程中,速度与磁场方向夹角时刻改变,所以,产生的电动势时刻改变,即产生交变电流.而焦耳定律Q=I2R t中的电流必须是有效值.
2 根据能量守恒定律求解
【例3】如图3所示,MN,P Q两条平行的光滑金属轨道与水平面成θ角固定,轨间距为d,空间存在匀强磁场,磁场方向垂直于轨道平面向上,磁感应强度为B,Q和N间接有阻值为R的电阻,质量为m的金属杆a b水平放置在轨道上,其有效电阻为r,现从静止释放a b,当它沿轨道下滑距离s时,达到最大速度.若轨道足够长且电阻不计,重力加速度为g.求:
(1)金属杆a b运动的最大速度;
(2)金属杆a b从静止到具有最大速度的过程中电阻R上产生的焦耳热.

图3
解析:(1)金属棒匀速时速度最大,此时满足B
I d =m gsinθ
而

所以

(2)由能量守恒得

而

所以

点评:金属棒先做加速度减小的加速运动,当安培力增大到m gsinθ时,开始做匀速运动.棒在加速的过程中产生变化的电流,并且无法求有效值,只能根据能量转化与守恒知识求解.
3 根据安培力做功求解
【例4】如图4所示,顶角为90 °的光滑金属导轨M ON固定在水平面上,导轨M O和NO的长度相等,M,N两点间距离l=2m,整个装置处于磁感应强度大小B=0.5T,方向竖直向下的匀强磁场中.一根粗细均匀,单位长度电阻值r=0.5Ω/m的导体棒在垂直于棒的水平拉力作用下,从MN 处以速度v=2m/s沿导轨向右匀速滑动,导体棒在运动过程中始终与导轨接触良好,不计导轨电阻,求:
(1)导体棒刚开始运动时所受水平拉力F的大小;
(2)导体棒通过整个金属导轨的过程中产生的焦耳热.

图4
解析:(1)导体棒开始运动时,切割磁力线产生的感应电动势为
E=Blv
导体棒所受安培力为
F安=BiL
由平衡条件得
F=F安
联立上式得

代入数据得
F=2N
(2)设棒经t时间运动位移为x,则t时刻棒切割磁力线的有效长度
lx=l-2x
由(1)问知
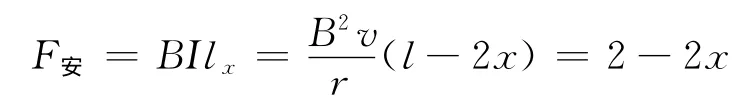
即安培力的大小与位移成线性关系,故安培力的平均值
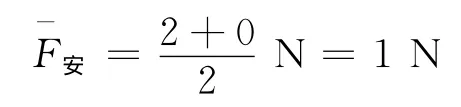
所以产生的焦耳热

代入数据得
Q=1J
点评:此题涉及动生电动势,导体棒在匀速切割磁力线的过程中,虽然其有效长度和回路电阻都在变化,但产生的电流却是恒定的,即

又因为回路电阻是变化的,所以无法根据焦耳定律Q=I2R t求解,但可以根据Q=W安求解.
4 结束语
综上可知,电磁感应的实质问题是能量的转化与守恒,这是求解焦耳热最基本的思路.只有对问题进行具体分析,弄清其物理过程和物理问题的本质,才能找到有效解决问题的方法.
当导体中产生的电流可以确定时,即回路中产生恒定电流或交变电流时,电流的有效值可以确定,就用焦耳定律Q=I2R t求解,否则就考虑能量守恒定律或安培力做功来求解.
