光的折射定律的理论分析与推导

梁 雄 赖国忠

（龙岩学院 福建 龙岩 3640 12 ）

1 引言

反射定律和折射定律是几何光学两个基本定律，可利用费马定理证明［1～3］，也有一些《工程光学》教材是利用电磁场的连续条件来分析平面光波在各向同性介质分界面上的反射和折射［4，5］．这些教材一般都是列出s波（电场强度在垂直入射平面方向的分量）满足电场强度切向连续的方程，然后，通过简单的观察和分析得出反射光波（或折射光波）的频率与入射光频率相等的有关内容，但是教学中发现，大多数学生对这样的探讨方式所得的结果疑惑不解，总觉得推导过程不够严密．现就在原有方程的基础上利用导数和矢量叉乘进行详细分析和推导．

2 折射定律有关内容的推导

图1 平面光波在界面处传播

如图1所示，一束光从折射率n1的介质1入射到折射率n2的介质2，电场矢量在垂直于入射面方向的分量称作s波，平行于入射面的分量称作p波，坐标系中y轴垂直纸面向外．根据电磁场的连续条件［6］列出电场的s波在界面处满足的方程［5］

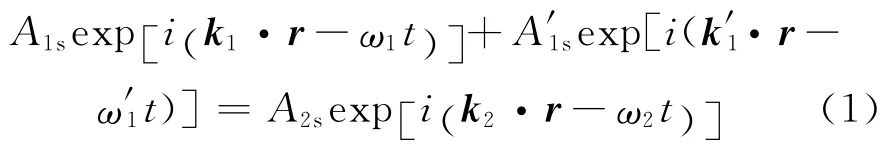
利用exp ［i（ α ＋β）］＝e x p（iα）e x p（iβ） 可 将 式 （1）中时间部分和空间部分分离，并令入射光、反射光和折射光中的s波复振幅分别为

A1＝A1sexp （i k1·r）

A′1＝A′1sexp （i k′1·r）

A2＝A2sexp （i k2·r）

即

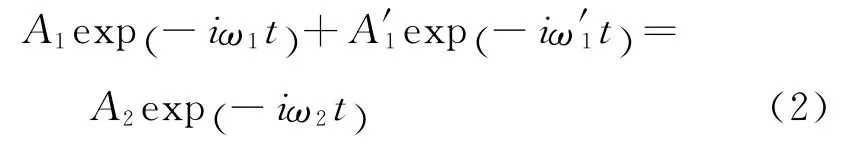
两边同除以e x p（－ i ω1t），整理可得

其中，Δω2＝ω1－ω2，Δω1＝ω1－ω′1．将式（3）对时间求一阶导数并化简可得

式（4）两边同除以exp （iΔ ω2t）得

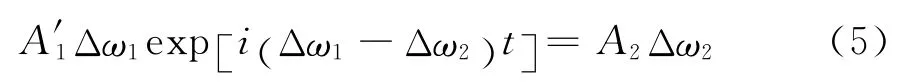
通常情况下，该方程中A′1≠0，A2≠0．观察方程（5）的两边会发现其右边与时间无关，而左边却含有exp ［i（Δω1－Δω2）t］时间因子，只存在两种可能，第一种，当Δω1＝0时，方程的左边为零（即与时间无关），这就要求方程的右边也为零，即有Δω2＝0；第二种，当Δω2＝Δω1时，则因子

exp ［i（ Δω1－Δω2）t］≡1

将这一结果代入式（3）并整理后可得

仔细观察式（6），其左边为一个不为零的常量，这就要求方程右边与时间无关，即有Δω1＝0．

综合上述两种情况均可得出同一个结论，即反射光束和折射光束的角频率都与入射光束的角频率相等，将其表示成数学表达式为

将式（7）代入式（1），两边同除以e x p［i（k1·rω1t）］化简得

其中N ＝k′1－k1，N′＝k2－k1．将算符

作用于式（8）两边可得

式（9）两边同除以N2exp （i N ′·r）得

式（10 ）的右边与位矢r无关，这就要求其左边也与r无关，即

将式（11 ）代入式（8）进行整理后得

式（12 ）的左边为一常量，这就要求右边与r无关，即N′·r＝0．结合式（11 ）易得

其中，r为界面（x y平面）上任意位矢．由立体几何知识可知，N和N′（或－N′）垂直界面，均可代表介质界面的法线．

下面利用矢量叉乘证明光的折射定律，证明过程中用－k1和k2分别代表入射光线和折射光线的位置，则入射角等于－k1与－N′之间的夹角θ1，折射角等于k2与N′之间夹角θ2，具体参见图2．结合矢量减法的特点分析不难得出，－k1，k2和法线N′（或－N′）在同一平面内．根据矢量叉乘容易验证下面的方程成立

图2 各波矢及有关的矢量

注意连等式（14 ）的中间表达式中出现一个负号，不难由“矢积的方向用右手螺旋法则确定”分析出－k1和k2分居法线两侧，即折射光和入射光分居法线两侧．式（14 ）的两边取模得

3 结论

针对现有教材通过简单的观察，对比方程（1）得出光的折射定律等有关内容，大多数学生对所得结论难以接受，本文借助于高等数学中的导数和矢量叉乘等加以适当推导，使得分析所得的结论更加一目了然，从而提高了课堂的教学效果．

1 姚启钧．光学教程（第3版）．北京：高等教育出版社，2006 ．153 ～156

2 宫彦军，王喜昌，宋东草，等．折射定律与反射定律的推导．物理实验，2005 ，25 （2）：41 ～43

3 杨春艳，刘飞，吉恒，等．折射定律服从费马原理的一种证明方法．玉溪师范学院学报，2010 ，26 （8）：27 ～28

4 田芊，廖延彪，孙利群．工程光学（第1版）．北京：清华大学，2007 ．17 ～19

5 郁益银，谈恒英．工程光学（第3版）．北京：机械工业出版社，2013 ．300 ～302

6 梁灿彬，秦光戎，梁竹健．电磁学（第3版）．北京：高等教育出版社，2012 ．108 ～109