基于重心驱动进给系统工作台动态性能分析*
2014-06-29王志军缑建文朱本辉
夏 田,王志军,缑建文,朱本辉
(陕西科技大学 机电工程学院,西安 710021)
0 引言
目前,机床高速、高精度、高效率的发展趋势,对机床的进给系统提出了越来越高的要求。进给系统作为数控机床的重要组成部分,其动态性能是影响加工精度的关键因素。直线电机、并联虚拟轴、重心驱动[1]等新的驱动方式和理论,是改进进给系统的主要方法理论。其中,重心驱动可以克服传统进给方式中由于附加力矩而产生的偏振现象使得运行更为平稳、位置响应精度更高[2],且改造成本低、技术相对容易实现,逐渐被推广应用。
以某高速数控机床十字滑台进给系统(Y轴)为基础,利用重心驱动理论对其进行双驱改进,建立了有限元分析模型,把工作台的动态位置响应作为研究对象,考虑了丝杠与螺母结合面的刚度和阻尼对工作台的影响,把导轨的间距作为设计的变量,通过模态分析确定了550mm 导轨安装间距在四组间距选择中总体刚度最优。进一步,给丝杠上施加额定的简谐力,取工作台上任意一点P比较了改进前后谐响应的位移幅值,仿真结果表明改进后对进给系统工作台位置精度影响大的进给方向(Y轴)和垂直方向(Z轴)动刚度有明显增加。水平方向(X轴)波动范围较小,可知工作台整体动态性能有一定的改进。
1 重心驱动进给系统动力学模型
针对Y驱动轴方向的双驱进给系统,如下图1 所示。主要有工作台、导轨、滑块、螺母和丝杠构成。A1、A2 为丝杠作用力作用点,B1、B2、B3、B4 为滑块与工作台的作用力作用点,G为工作台的重心。假设工作台在力的作用下发生了一个小的位移,转角为α、β、γ。忽略各方向的振动耦合,则根据通用的系统动力学方程可以得到工作台进给系统的动力学模型:
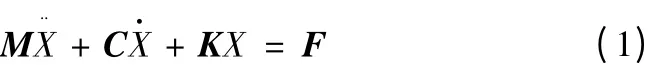
式中,X=[x、y、z、α、β、γ]’为位移和转角变量,M 为质量矩阵,C 为阻尼矩阵,K 为刚度矩阵,F 为力和力矩矩阵。假定导轨和螺母关于工作台对称分布。lA、lB分别为螺母和滑块X轴方向距工作台重心G的距离,hA、hB,分别为两者Z轴距重心G的距离,sA、sB为Y轴距重心G距离。
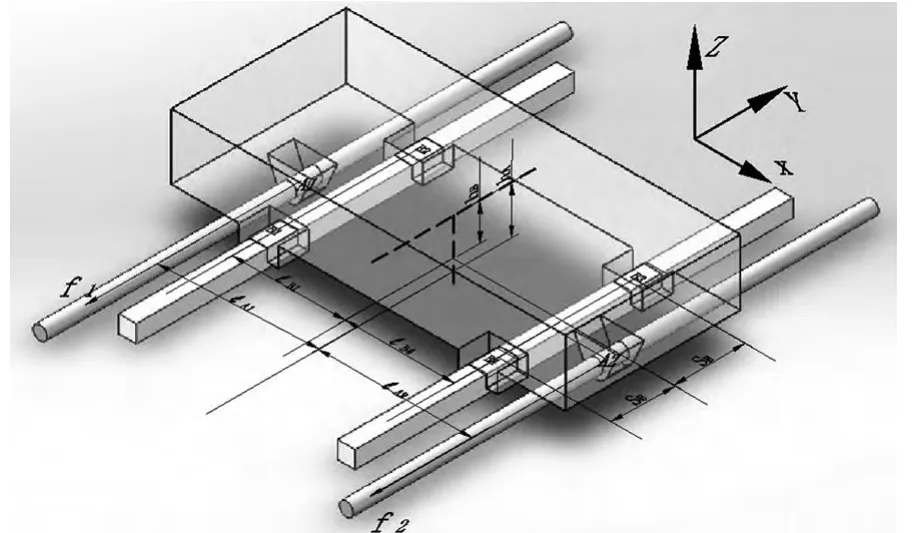
图1 双驱进给系统结构图
式中,M 为质量矩阵,C 为阻尼矩阵,K 为刚度矩阵,F为力和力矩矩阵。假定导轨和螺母关于工作台对称分布。lA、lB分别为螺母和滑块X轴方向距工作台重心G的距离,hA、hB,分别为两者Z轴距重心G的距离,sA、sB为Y轴距重心G距离。m和IX、IY、IZ为工作台组件的质量和三个方向上的转动惯量,CX、CY、CZ和Cα、Cβ、Cγ为滑块与导轨的三个方向的平动阻尼和转动阻尼。则M、C、K 的表达式可以表示为:

暂时不考虑阻尼对进给系统的影响,根据理论力学可知F=[0f1+f20 -(f1+f2)hA0 0]',则对上式进行拉斯变化可得:
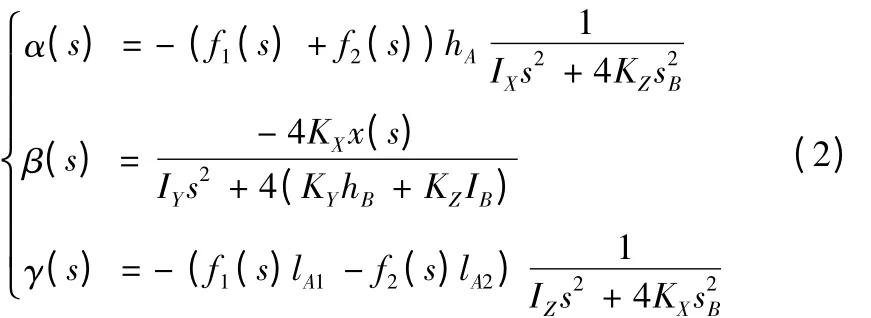
从式(2)可以看出对双驱进给系统,位置响应的主要因素是驱动力平面与工作台组建重心平面的距离hA,其值越小则驱动力引起的扰X轴的扭转量就越小,f1lA1-f2lA2值越小引起的扰Z轴的扭转量就越小。理论上的重心驱动力矩设计是使两者的值都趋近与0,这样可以消除由于力矩引起的偏振现象,从而使得驱动过程更平稳,位置响应精度更高。鉴于此,改进后模型驱动丝杠安装在工作台的两侧,尽可能的使其等效虚拟驱动力通过工作台的重心。改进前后进给系统结构如下图2 所示。
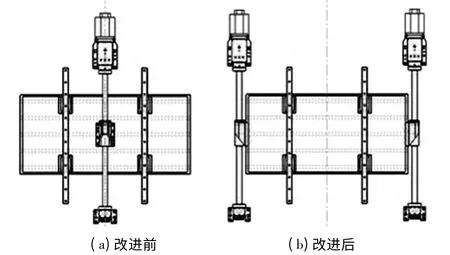
图2 进给系统结构图
2 模态分析
2.1 建立有限元模型
建立精确的有限元分析模型需要做好模型简化、网格划分、结合面建模、边界条件设定等。模型简化包括去除空洞、倒角、和对分析影响不大的部件,简化后的模型可以利用ANSYS 与三维软件的接口直接导入到Workbench 或者转化Workbench 可以识别的中间格式导入,简化后的模型如图3。网格的划分采用设置网格尺寸的智能网格划分方式。结合面的建模主要分三个部分考虑。第一部分固定接触,包括工作台与滑块连接、螺母与滑块连接;第二部分,忽略阻尼的滑动接触,滑块与刀轨的连接;第三部分,螺母和丝杠的链接。根 据 结 合 面 建 模 的 原 理[3],Workbench 中 用springs 模拟螺母和丝杠链接,刚度和阻尼根据具体的丝杠参数确定。螺母与丝杠的预紧力有轴向的刚度和阻尼模型,建立的丝杠与螺母的动力学模型如下图4所示。边界条件包括刀轨底面、丝杠两端的固定约束。
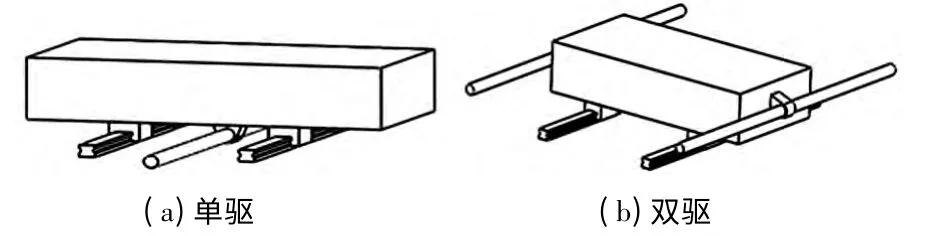
图3 有限元分析简化模型
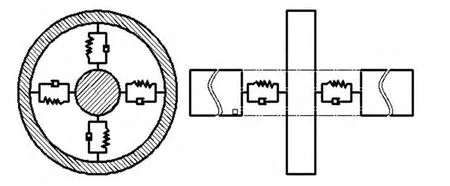
图4 螺母丝杠结合面的动力学模型
2.2 模态分析
模态分析是用来确定结构或构件的振动特性,即固有频率和振型。在承受动态载荷的结构设计中,它是重要参数。通过模态分析可以获取结构动力特性为优化设计提供依据。采用Workbench 默认的Block Lanczo 法对装配体进行模态分析。导入简化模型、设置模型材料参数、划分网格、接合面建模、添加边界条件、输出设置、求解。可以获取进行系统工作台前n阶固有频率和振型。表1,为改进前单驱和改进后不同导轨间距条件下进给系统工作台的前6 阶固有频率,图5 为刀轨间距550mm 双驱进给系统工作台振型图。
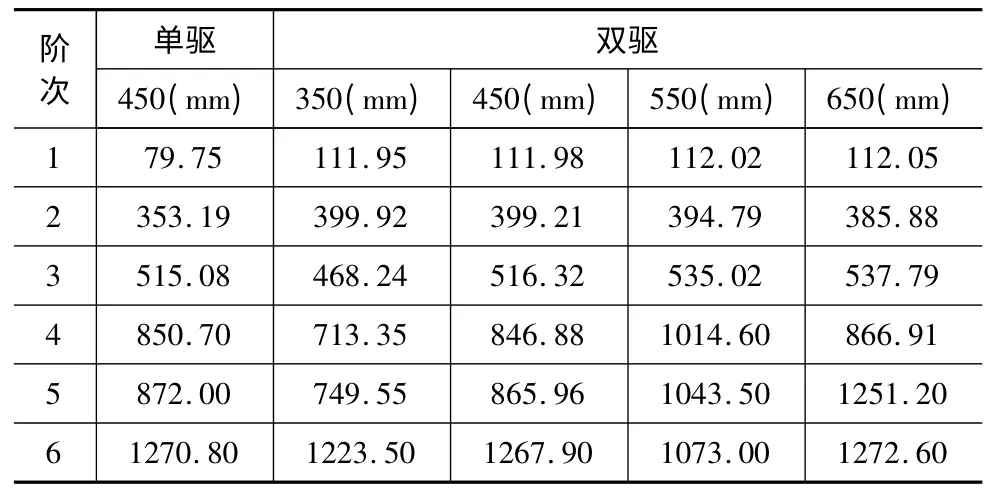
表1 进给系统前6 阶固有频率
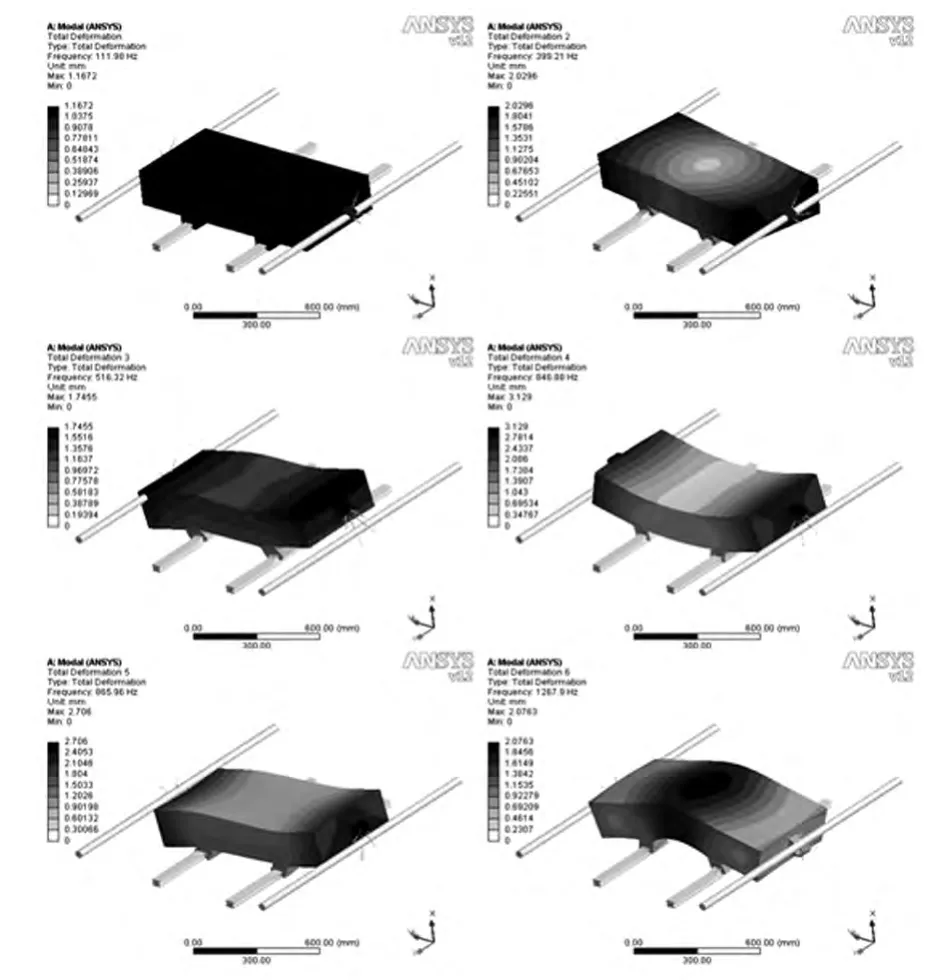
图5 双驱进给系统工作台振型
比较振型图可知,单驱进给系统工作台和导轨分别为350mm、450mm、550mm 间距的双驱进给系统工作台的前6 阶振型基本相同。1 阶主要表现为工作台Y轴的轴向振动,2 阶主要表现为滑块和工作台绕Z轴转动,3 阶主要表现为绕Y轴的转动,4 阶振型表现为工作台的绕X轴转动和翘曲,5 阶主要表现为工作台绕X轴转动,6 阶主要表现为工作台Z轴方向的振动。双驱导轨间距650mm 进给系统工作台振型顺序发生了较大变化,Z轴方向的振动固有频率提前,绕X轴转动和翘曲的固有频率增加。对比相同间距下单驱和双驱的低阶固有频率,可以看出1、2 阶频率有大幅度的提高,说明双驱进给系统提高了工作台进给轴向刚度和径向的扭转刚度。随着双驱进给系统导轨间距的增大,表现为滑块的扭曲和工作台的径向转动的2阶故意频率逐渐降低且降幅逐渐增大。表现为Z轴振动和X轴转动的频率先增后减。以上可知,恰当的选择导轨的间距对提高工作台的动态响应性能有重要的作用。综合考虑,选用间距为550mm 的丝杠布局为最优选择。
3 谐响应分析
在模态分析的基础上,利用Workbench 提供的模态叠加法,对改进前后的的模型进行谐响应分析。通常进给系统在进给方向刚度最为薄弱[5-6],进给过程中的波动干扰力对系统的精度影响较为明显。因此,假定Y轴方向存在200N 简谐干扰力,作用力等效作用在滚珠丝杠上。选取工作台表面的任意一点点P,输出0~1250Hz 范围内的三个坐标轴方向的谐响应曲线。图6 为改进前的单驱响应曲线,图7 为改进后的双驱响应曲线。

图6 改进前的幅频位移曲线
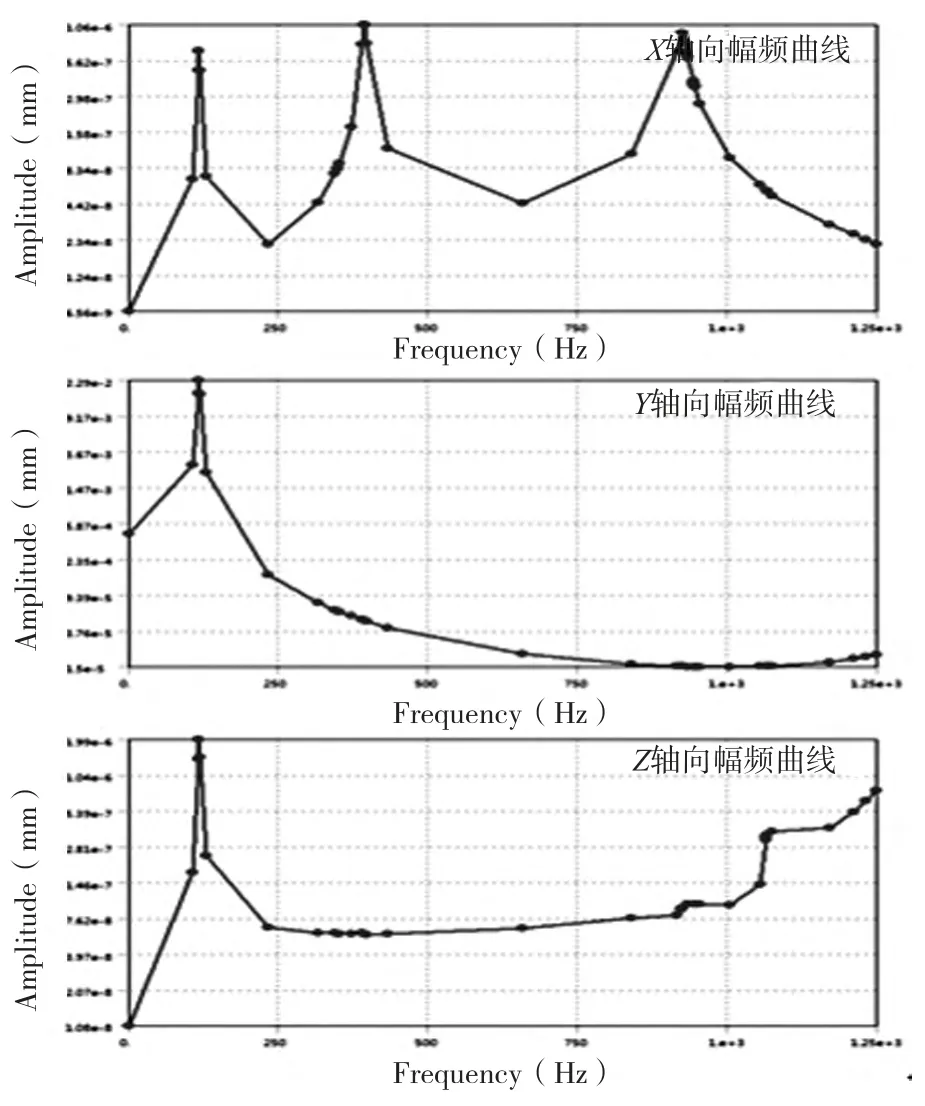
图7 改进后的幅频位移曲线
通过响应曲线可知单驱情况下X轴的最大振幅为4.57×10-7mm,对应于单驱进给工作台的第一阶模态,说明工作台的Y轴方向刚度对工作台X轴向的精度有较大影响,振幅数量级较小,可知X轴方向总体刚度较高,对系统的位置精度影响较小。双驱情况下X轴的最大振幅为1.06×10-6mm,对应于工作台第二阶模态,且前两阶模态对应的响应幅值基本相同,可知低阶共振是影响X轴向进度的主要因素。对比两者,可知双驱对工作台的X轴向动刚度影响不大,相反有所增加,分析是由于导轨间距变化和双驱简谐力产生的绕Z轴力矩导致的。Y轴的最大振幅均对应于两者的第一阶模态,单驱幅值为4.55×10-2mm,双驱为2.29 ×10-2mm。双驱幅值减少了49.6%,说明双驱情况下Y轴的进给动刚度有较大提高,且对精度影响比较明显。Z轴的最大振幅同样对应于在第一阶模态,单驱的最大振幅为1.02 ×10-4mm,双驱为1.99 ×10-6mm。分析可知双驱情况下消除了绕X轴的力矩提高了Y轴的刚度,可以显著提高Z轴方向的位置精度。
4 结论
基本重心理论对某高速数控机床Y轴进给系统进行双驱改进,建立了有限元分析模型,分析了对位置响应的关键因素;利用Workbench 对改进前后有限元模型进行模态分析,得出550mm 导轨间距的双驱工作台综合刚度最优;通过对改进前后的模型进给谐响应分析得出进给轴Y轴刚度是影响位置精度的关键因素。双驱改进后提高了进给系统的进给刚度,提升了进给系统的动态性能。
[1]张伯霖,黄晓明,范梦吾. 高速数控机床三种进给系统的分析与评价[J]. 世界制造技术与装备市场,2003(2):89-93.
[2]周勇. 高速进给驱动系统动态特性分析及其运动控制研究[D].武汉:华中科技大学,2008.
[3]翁德凯,程寓,夏玲玲,等. 基于结合面的立式加工中心进给系统的动态特性分析[J]. 机械设计与制造,2012(3):130-132.
[4]杨晓君,赵万华,刘辉,等. 直线电机进给系统机械系统动态特性研究[J]. 西安交通大学学报,2013(4):44 -50.
[5]许向荣,宋现春,姜洪奎. 提高数控机床滚珠丝杠进给系统机械刚度的措施[J]. 组合机床与自动化加工技术,2008(8):1 -4.
[6]王培功,彭伟,翁泽宇. 数控机床进给系统的动态优化设计[J]. 机械设计与制造,2005(8):101 -103.
[7]杨军,吕露,王凯,等. 基于ANSYS 的装配体的模态分析[J]. 汽车实用技术,2011(5):24 -26.
[8]夏田,柳鹏,蒋晓阳,等. 基于Adams 高速数控平台的动态响应性分析[J]. 煤矿机械,2012(4):111 -113.
[9]弋江淼,高东强,张菲,等. 基于ANSYS Workbench 的DVG850 工作台系统的模态分析及优化[J]. 制造业自动化,2012,34(12):55 -56.
[10]胡俊. 重心驱动工作台动力学建模及其特性分析[D].武汉:华中科技大学,2007.
[11]赵万军. 基于ANSYS 的滚珠丝杠进给系统静动态特性分析[J]. 机械传动,2010(5):68 -70.
