基于实时更新神经滤波及其光学实现的复杂零部件特征并行检测算法

刘向娇，毛红阁

(南阳师范学院 软件学院，河南 南阳 473061)

0 引言

随着计算机科学与信息理论的不断发展和完善，图像处理已经在日常生活中占据着重要地位［1］。图像边缘检测作为图像处理的重要方向之一，也是当前的研究热点，在机械、医疗以及国防领域得到广泛应用［2］。图像边缘包含着其本身的诸多纹理，其检测精度决定了图像处理质量。而传统的边缘检测算子，如Canny 算子、Sobel 算子以及Log 算子等，这些算子的检测精度较低，难以满足日益复杂图像的需求［3］。为了更好的检测图像边缘，诸多学者设计了一系列新颖的边缘检测算法。如郑英娟［4］等人为了解决传统边缘检测算法的不足，设计了基于八方向Soble 算子的边缘检测算法，检测出图像的各个方向边缘，并根据领域到中心像素的欧氏距离进行检测，实验结果表明其算法具有良好的检测效果，检测边缘完整，轮廓清晰。薛武［5］等人基于Canny 算子，通过对梯度模值的内插求得沿边缘点梯度方向上相邻像素的梯度模值，利用这些梯度模值拟合二次曲线求出其极大值得到子像素定位的精确位置，提出了Canny 算子子像素边缘检测算法，并对其算法进行了实验验证，结果显示其算法具有较高的检测精度，检测边缘清晰完整。谢妍梅［6］等人针对彩色图像，根据人类视觉特性，引入HIS 颜色空间，设计了基于HIS 颜色空间的彩色图像边缘检测算法，根据色度和饱和度的相关性改进色差度量方法，设计边缘生长方法以保证边缘连续性，结合4 个分量的边缘信息得到最终边缘检测结果，并对其算法进行了实验验证，结果表明其算法可有效消除噪声影响，边缘检测精度高。

复杂零部件是制造业领域内最常见的零件之一，在航空、机械以及汽车行业有着重要地位。而其主要特征，如边缘轮廓以及平整度，是自动化精密加工的重要指标。因此，提取优异的复杂零部件特征，对精密加工有着重大影响。而在复杂零部件图像的采集期间，其容易遭受到周围环境、CCD 自身噪声等诸多因素污染，降低了其质量，为后续检测带来不便。这些复杂的环境增加了牙型边缘检测的难度。目前，诸多学者将边缘检测思想用于部件特征提取，取得了较好的效果［7-9］。但是这些算法难以用于复杂零部件特征提取，特别是表面的微凹坑以及曲面处;且这些算法的检测效率较低，都是非并行模式，增加了其检测成本。

对此，本文基于Hopfield 神经网络，构造自适应滤波掩码，并嵌入2D 卷积运算，设计了实时更新神经滤波技术及其学习算法，使得本文算法以并行模式检测复杂零部件图像的特征;并建立了神经滤波的光学实现结构，执行动态神经滤波，提高其检测效率，从而提出了基于实时更新神经滤波及其光学实现的复杂零部件图像特征并行检测算法。最后，利用仿真技术测试了本文算法的性能。

1 本文复杂零部件图像特征检测算法

本文复杂零部件图像特征检测算法流程见图1。从图中可知，该算法主要包括三个步骤:①实时更新神经滤波设计;②学习算法调整滤波系数，优化检测边缘;③动态神经滤波的光学实现。

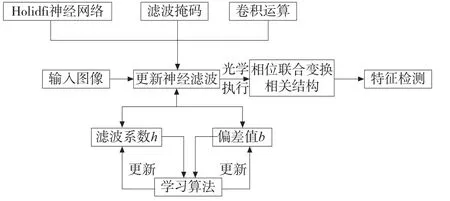
图1 图像特征提取算法示意图

1.1 实时更新神经滤波结构设计

引入Hopfield 神经网络，其结构如图2 所示。从图中可知，Hopfield 神经网络利用输入矢量来初始化神经元，随后不断迭代，知道输出收敛。当神经网络正确运行时，其输出结果应为初始矢量之一。故Hopfield 神经网络实质是将择取的原型视为输出结果，其公式为:

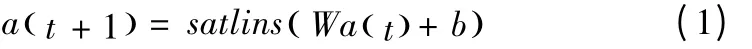
其中，a( 0) 为初始输入图像;a(t) 代表第t次迭代输出结果;W为权重矩阵;Satlins为线性传递函数，见图1 中的f∈[-1，1] ;b为扰动值;t为迭代次数。

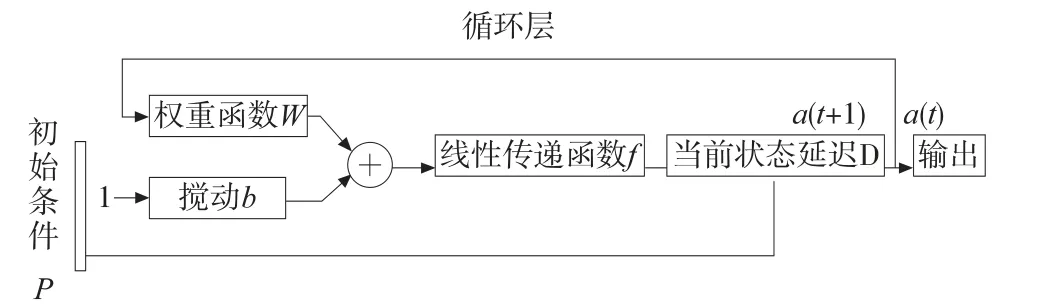
图2 Hopfield 神经网络

为了提高检测效率，降低大容量权重矩阵与网络输出之间的加权求和操作的复杂度，本文构造3×3 滤波掩码来替代权重系数矩阵W，见图3a。并嵌入2D卷积运算，来替代权重系数与网络输出之间的矩阵乘积，见图3b。从而设计了实时更新神经滤波，见图4。从图4 可知，实时更新神经滤波的循环过程为输入与滤波掩码的卷积运算，其模型设计如下:

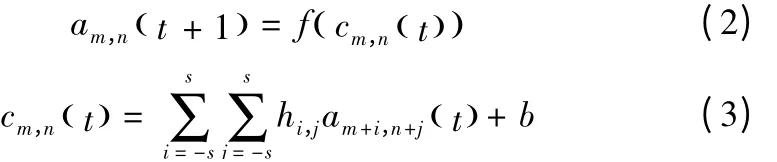
其中，f为非线性激活函数;t为迭代次数;代表系统输出;hi，j为尺寸s × s的滤波掩码;b代表标准偏差值;am，n(t) 为输入值。定义初始输入图像为:

并将动态神经滤波的输入和输出定义为激活函数:

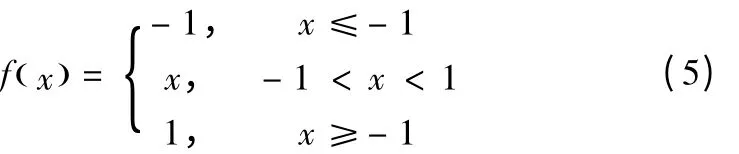
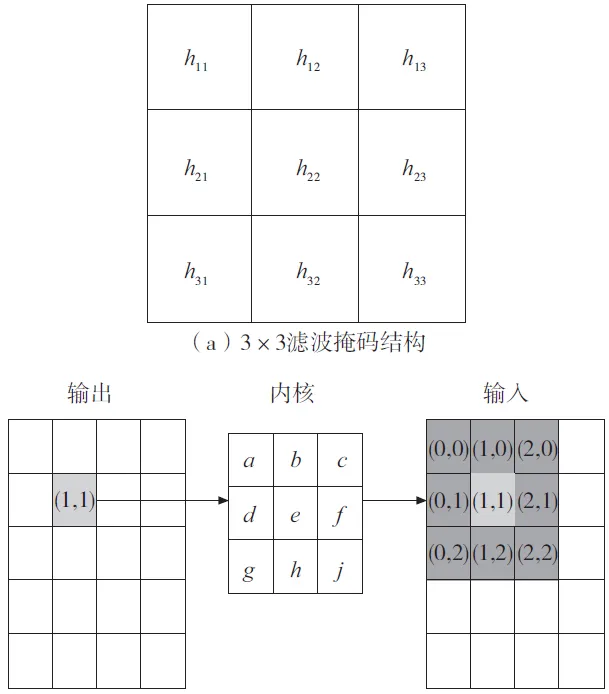
图3 算法相关结构

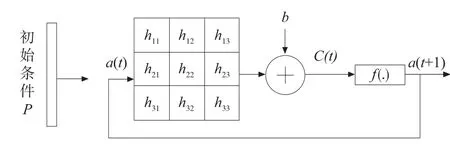
图4 实时更新神经滤波结构

1.2 学习算法

为了调整动态神经滤波系数，本文设计了该技术相应的学习算法。为了最小化理想输出与实际输出图像之间的差异，构造如下函数:

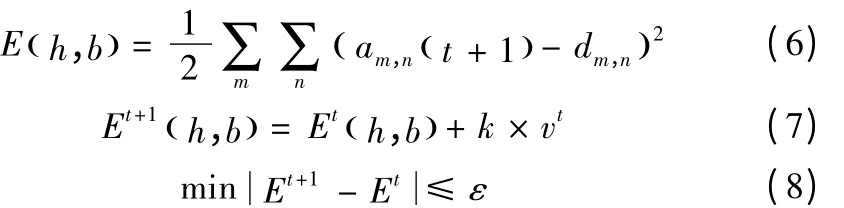
其中，E(h，b) 为误差函数;am，n代表实际输出图像;dm，n为理想输出图像;k为搜索步长;v为搜索方向。

利用公式(7)和(8)循环迭代，使得误差逼近最小。在最小化E(h，b) 后，得到的更新滤波系数和偏差值为:

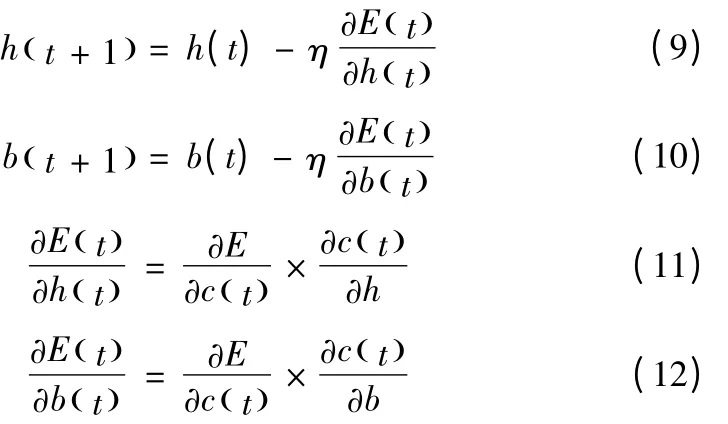
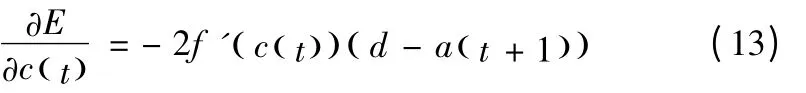
其中，f '代表模型(5)中的激活函数的偏导数;表实际输出图像;d为理想输出图像

最后，再将更新的滤波系数和偏差值代入(9)和(10)中，得:

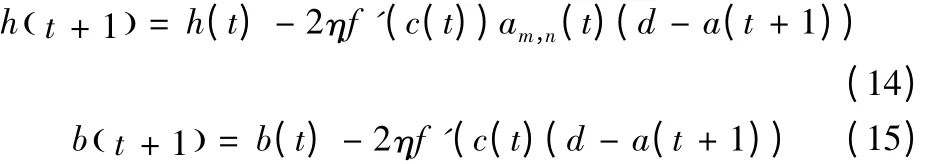
根据模型(14)和模型(15)可知，本文设计的学习算法是连续迭代过程，当学习算法收敛于时，最新的滤波系数和偏差值会保存在测试相中。

1.3 动态神经滤波的光学实现

依据获得的最新的滤波系数和偏差值，借助联合变换相关结构(见图5)来实现模型(3)中的交叉相关。在联合变换相关结构中，联合输入图像看定义如下:

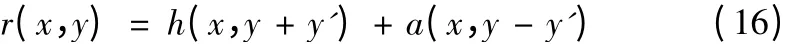
其中，r(x，y)为联合输入图像;h(x，y + y')代表滤波掩码;a(x，y - y')为输入图像。

根据模型(1)，可得r(x，y)的相关输出图像:

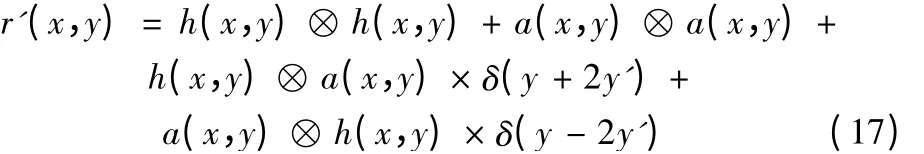
模型(17)最后两项就是h(x，y) 与a(x，y) 的交叉相关。为了能够在输入和傅里叶平面上编码双极数据(正和负)，运用如下定义的函数:

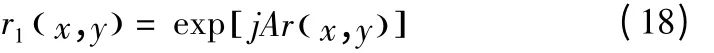
其中，A代表相位深度或者转换效率，其值一般为A=π/255 or 2π/255;

傅里叶平面域为:

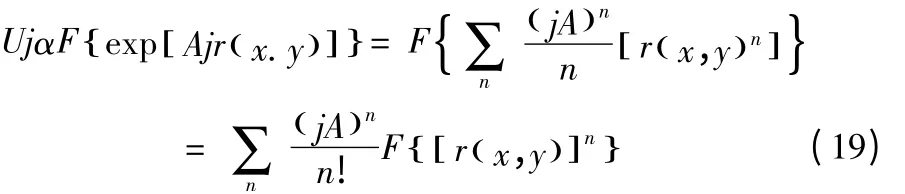
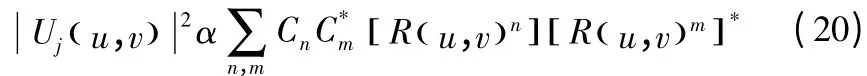
其中，u，v代表与x，y方向相关的空间频率;* 代表共轭运算。

再次运用傅里叶变换，得到相关面强度为:

其中，⊕为卷积运算。

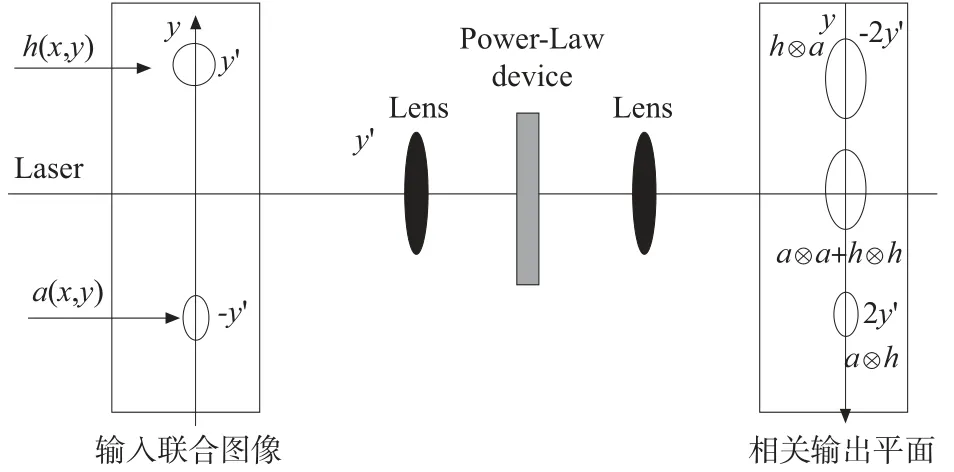
图5 更新神经滤波的光学实现结构

2 仿真结果及分析

为了体现本文算法性能，设立对照组:文献［10］以及文献［11］，分别记为A、B 算法。借助MATLAB软件来测试本文算法性能。测试对象，见图6a。仿真条件为:采用因特尔T7，2.5GHz 双核CPU，400GB 硬盘，8GB 的内存，Windows xp 运行系统。利用本文并行检测算法以及对照组对复杂零部件图像特征进行检测。

2.1 特征提取质量对比分析

不同算法检测复杂零部件特征效果见图6。从图6 中可知，本文算法的检测效果非常理想，复杂零部件轮廓连续完好，且曲面处以及表面微形貌清晰可见，见图6b 箭头所示;而A、B 算法的视觉效果不佳，在曲面连接处出现不连续，且无法检测出表面微形貌;图7 也有相同的效果。

为了更加清晰体现复杂零部件表面情况，对图6b～6d 和图7b～7d 进行拓扑凸显。仿真结果见图6e～6g 和图7e～7g。从图6e 与图7e 中可知，复杂部件表面纹理与边缘轮廓清晰可见。

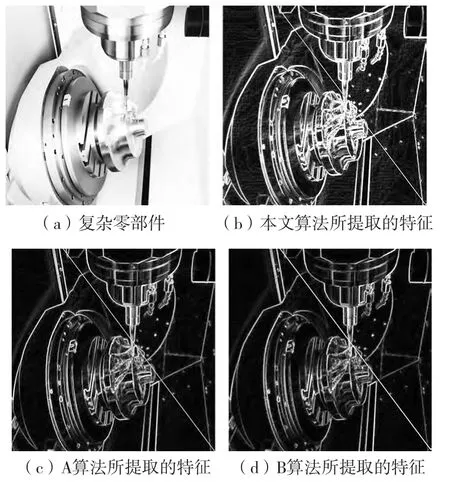
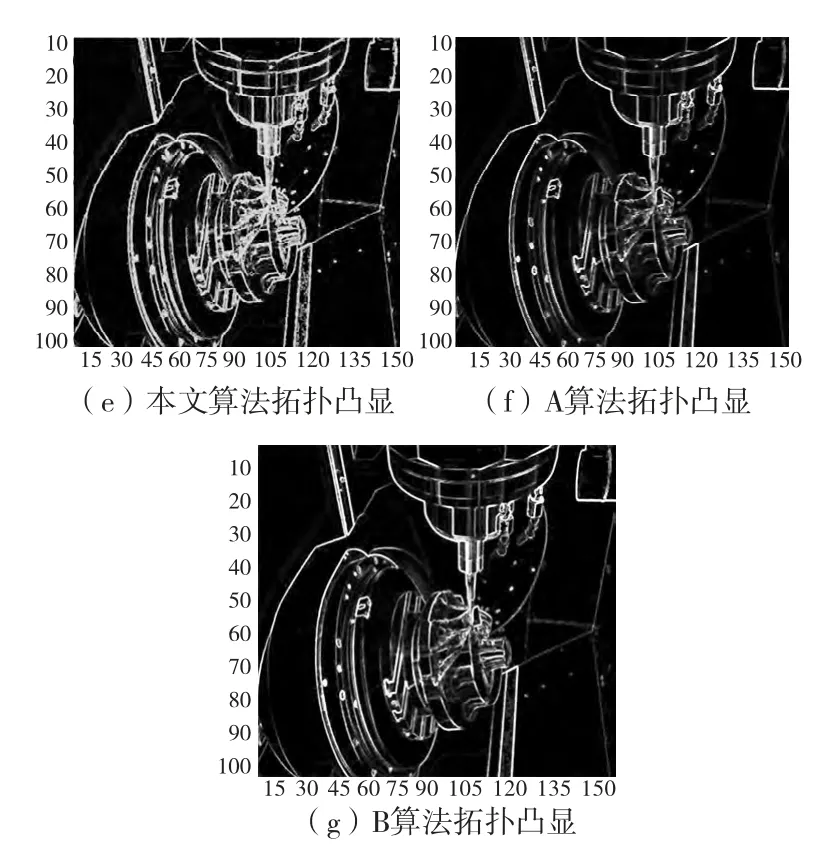
图7 不同特征提取算法及拓扑凸显仿真结果图

2.2 检测精度对比

对图6a 的曲面连接处的角点进行检测，结果见图8。从图8 中可知，本文算法的检测精度最高，曲面连接处的角点很丰富;而A、B 算法的检测精度较低，部分曲面连接处角点稀疏。这表明本文算法具有更高的检测精度。原因是本文算法设计了学习算法，使得检测结果不断优化。

图8 不同特征提取算法的角点检测结果

2.3 检测效率对比

以本文2.2 节中的角点检测为实验对象，测试其效率，结果见表1。从表中可以看到，本文算法的检出率最高，且时耗较短;而A、B 算法的检出率与效率均不理想。原因是本文算法设计了动态神经滤波及其光学实现，使得算法以并行模式进行检测，继而显著提高了检测效率;而A、B 算法都是非并行模式，增加了检测成本。

表1 角点检测效率测试结果

3 结论

针对当前的边缘检测算法难以用于复杂零部件特征提取，易造成曲面处轮廓不连续，无法检测表面形貌;且检测效率不佳，是一种非并行模式，增加了其检测成本。基于Hopfield 神经网络，设计了实时更新神经滤波技术及其学习算法，利用学习算法更新滤波系数与偏差值;并建立了该技术的光学联合转换结构，完成神经滤波的光学实现，以并行模式提取复杂零部件边缘，并提高其检测效率;最终提出了基于实时更新神经滤波及其光学实现的复杂零部件特征检测算法。仿真结果显示:该算法具备较佳的检测质量;与当前边缘检测机制相比，本文算法的检测精度更高，曲面处轮廓连续完整，无视觉不连通现象;且该算法的检测效率更高。

［1］Abdullah AH，Enayatifar R，Lee M .A hybrid genetic algorithm and chaotic function model for image encryption［J］.AEU:Int JElectron Commun，2012，66 (10):806 -16.

［2］K Bhardwaj，PS Mann. Adaptive Neuro-Fuzzy Inference System(ANFIS)Based Edge Detection Technique［J］. International Journal for Science and Emerging，2013，8(1):7-13.

［3］K Ray. Unsupervised edge detection and noise detection from a single image ［J］. Pattern Recognition，2013，46(8):2067 -2077.

［4］郑英娟，张有会，王志巍，等. 基于八方向Sobel 算子的边缘检测算法［J］.计算机科学，2013，40(11A):354-356.

［5］薛武，张永生，董广军，等. Canny 算子子像素边缘检测方法［J］.遥感信息，2013，28(1):8 -11.

［6］谢妍梅，樊臻，张森林. 基于HSI 颜色空间的彩色图像边缘检测［J］.计算机工程，2013，39(9):12 -14.

［7］杨攀，姜立军，李哲林. 基于机器视觉的螺纹零件头部裂纹检测［J］.计算机应用与软件，2013，30(4):51 -54.

［8］吴德刚，赵利平. 基于机器视觉的圆孔尺寸测量系统研究［J］. 应用光学，2013，34(6):1014 -1018.

［9］YG Wei，ZX Wang. Research of Automatic Measurement Technology for Oil Thimble External Thread Parameters［J］.Key Engineering Materials，2014，579(123):558 -563.

［10］MN Syed，PM Pardalos. Neural network models in combinatorial optimization［J］. Handbook of Combinatorial Optimization，2013，127(54):1237 -1248.

［11］黄海龙，王宏，纪俐. 基于局部模糊增强的顺序形态学边缘检测算法［J］. 仪器仪表学报，2013，33(11):2608-2614.