基于六量子态的高容量量子秘密共享方案

许 娟 陈汉武 刘志昊 袁家斌

(1南京航空航天大学计算机科学与技术学院，南京210016)

(2东南大学计算机科学与工程学院，南京210096)

由于具有理论上的无条件安全性和窃听的可检测性，量子保密通信成为计算机科学和物理领域的一个重要研究方向.量子保密通信中研究最早、最成熟的是量子密钥分配(quantum key distribution，QKD)［1］.随后，学者们开始研究如何利用量子特性实现多方之间共享经典密钥［2-10］，即量子秘密共享 (quantum secret sharing，QSS).QSS可分为共享经典信息和共享量子信息两大类.

最初的QSS方案是基于多粒子纠缠态的［2］，但其制备较为困难［11］.因此，研究者们提出了基于单粒子态的多方 QSS 方案［3-6，9，10］，且大多借鉴了经典秘密共享中逐位异或的思想［3-5］.文献［3］介绍了一种直接对量子密钥分配中的量子比特进行编码实现秘密共享的方案，制备方发送N个单光子给n位接收方，接收方测量之后将结果逐位异或，得到要共享的经典密钥;如果忽略用于检测的光子，则制备方和接收方之间共享了N/n bit经典信息.文献［4-5］所提方案同样只能共享N/n bit经典信息.为了提高一方到多方QSS方案的量子比特容量，本文提出了一种基于六量子态的新方案，摒弃了对量子测量结果逐位异或的方法，具有容量高、所需量子资源少的优点.在该方案中，发送方负责对单光子进行制备和测量，n位接收方仅需要进行本地的酉操作，因而特别适用于发送方的设备条件远超过接收方的情况.

1 一方到多方QSS方案

假设发送方Alice要将一个二进制秘密A0=发送给Bob 1，Bob 2，…，Bob n(n≥2)，并希望只有n位Bob一起合作时才能得到这个秘密，任意m位Bob(m＜n)不能得到该秘密.基于六量子态的高容量QSS方案示意图见图1.图中，Ai为二进制串;Bi为三进制串;A0为要共享的秘密.

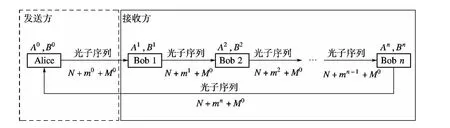
图1 基于六量子态的高容量QSS方案示意图

所提方案的具体步骤如下.

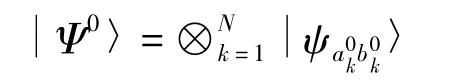
显然，每个光子为如下6个态之一:

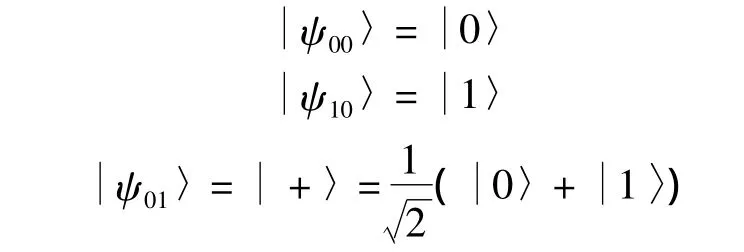
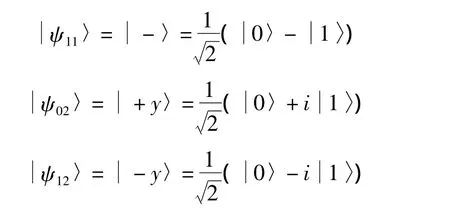
随后，Alice随机地插入足够的m0+M0个诱骗光子，这些诱骗光子随机处于6个态之一.最后，Alice将N+m0+M0个光子在公开的量子信道上传送给Bob 1.

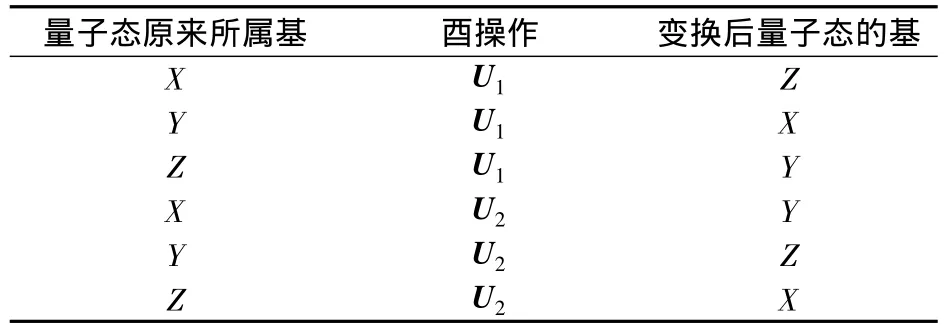
表1 U1和U2的作用

②Bob 1声明接收到所有光子信号之后，Alice公布其中m0个诱骗光子的位置.然后，Bob 1对这些位置上的光子首先使用一个特殊的过滤器来避免不可见光子进入操作系统，再用一个半透半反的光子数分裂器来分裂每一个信号.如果在一个信号中探测到多个光子，则Bob 1宣布终止本次秘密共享过程，否则Bob 1随机地使用X基、Y基或Z基对分裂后的信号进行测量，并将测量结果告诉Alice，同时丢弃这m0个诱骗光子.Alice分析测量基选择正确的那些测量结果的错误率，如果错误率高于某个阈值，则Alice宣布取消此次通信;否则，Bob 1产生随机的二进制串和三进制串Bob 1根据的取值(0或1)，对第k个光子进行I或σz操作，再根据的取值(0，1 或 2)，对第k个光子进行U0，U1或U2操作.最后，Bob 1随机地插入足够的m1个诱骗光子，这些诱骗光子随机处于式(2)所示的6个态之一.

③Bob i(2≤i≤n)声明接收到所有光子信号后，Bob(i－1)公布诱骗光子的位置.然后，Bob i执行与步骤②相同的操作，此时Bob i将诱骗光子的测量结果发给Bob(i－1)，而不是Alice，由Bob(i－1)进行错误率分析.这一过程由Bob i(2≤i≤n)依次执行，共执行n－1次.

④Bob n将N+mn+M0个光子发送给Alice.Alice声明收到所有光子后，Bob n公布诱骗光子的位置.然后，Alice对这些位置上的光子随机地使用X基、Y基或Z基进行测量，并将测量结果告诉Bob n，同时丢弃这mn个诱骗光子.Bob n分析测量基选择正确的那些测量结果的错误率，如果错误率高于某一阈值，则Bob n宣布取消此次通信;否则，所有Bob公开宣布的值.

⑦Alice公布最初插入的M0个诱骗光子的位置.Alice和所有Bob比对这些位置上得到的初始秘密值，如果错误率高于某一阈值，则丢弃该秘密;否则，剩下的二进制串即为要共享的秘密.

2 安全性分析

尽管理论上量子保密通信可以达到无条件安全，但是如果量子通信方案考虑不周或设备存在隐患，则通信过程和机密数据仍有可能被某些巧妙的量子攻击方法成功窃听而不被发现.因此，对于QSS方案来说，保证安全性是首要目标.

在本文方案中，Alice和Bob 1，Bob(i－1)和Bob i(2≤i≤n)，Bob n和Alice之间的通信过程与BB84 QKD方案类似［1］，相当于独立的n+1个BB84 QKD过程.BB84协议被证明是无条件安全的［12］，故本文方案理论上也是安全的.下面针对几种常见的量子攻击方法进行进一步的安全性分析.

1)不可见光子攻击［13］.窃听者Eve选择一些对发送方和接收方所用单光子探测器不敏感的光子，获得通信者的编码信息.在本文方案的步骤②和③中使用了特殊的滤光器来避免不可见光子进入接收方的操作系统，如果Eve的窃听光子没有被滤光器过滤掉，则将被接收方的光子探测装置探测到.

2)特洛伊木马攻击［14］.Bob i将一个多光子信号序列而不是单光子序列发送给Bob(i+1)，以通过多个光子副本得到Bob(i+1)的编码信息.本文方案在步骤②和③中使用了一个半透半反光子数分裂器来检测是否存在特洛伊木马攻击.如果在多个单光子探测器上同时发现有光子存在，则存在该攻击.

3)截获-重发和篡改攻击.在 Alice，Bob 1，Bob 2，…，Bob n将光子序列分别发送给Bob 1，Bob 2，…，Bob n，Alice的过程中，窃听者Eve截获光子序列，并重发一串光子给接收方;或者Eve直接对截获的光子进行篡改.显然，在本方案的步骤②～④中，发送方和接收方通过比对诱骗光子的测量结果来防止这2种攻击.

4)谎报攻击.Bob i谎报自己的Ai和Bi，以使其他Bob不能获得秘密信息而仅有自己能获得.在步骤⑦中，通过样本检测可以防止这种谎报攻击.

5)单光子攻击［15］.Bob n从Bob(n－1)处得到N+mn－1+M0个光子，并通过诱骗光子比对后，保留剩下的N+M0个光子序列，然后根据随机产生的An'和Bn'制备一个含有N+M0个光子的序列，并将发给 Alice;假设所有Bob按顺序公布Bi，则Bob n公布自己的三进制串，然后按照的结果去测量，以获得并躲过安全检测.显然，单光子攻击对本文方案是不适用的.这是因为Alice首先对光子进行了操作，A0和B0对于Bob n来说是无法获得的，即不能根据确定正确的测量基，故Bob n也就无法获得的值.

3 适用性分析

目前，制备纠缠态的效率较低，制备成本较高［11］，从而制备量子资源的代价远远大于制备经典资源的代价.一些多方QSS方案利用测量量子位后将结果逐位异或的思想［3-5］，假设制备方制备了N个单光子，并将其发送给n位接收方，忽略用于检测的光子，则制备方和接收方之间仅能共享N/n bit的经典信息.而本文方案不需要将量子比特的测量结果进行逐位异或.发送方Alice只需将量子比特的测量结果与自己的二进制串A0对应位的值进行异或，并公布该值;接收方只需将Alice公布的值和各自的二进制串Ai(1≤i≤n)对应位的值进行异或，即可获得要共享的秘密.在文献［6］中，定义量子比特容量为制备1个量子比特能共享的经典比特位数(忽略用于检测的量子比特)，即

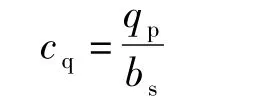
式中，qp为制备的量子数;bs为双方共享的经典比特数;0＜ cq≤1.文献［3-5］中，对于 QSS协议，cq=1/n;本文方案中，cq=1.量子比特容量可以用于衡量一个QSS方案需要量子资源的相对量.量子比特容量越大，所需的量子资源越少.由于量子资源的制备代价比经典资源的制备代价高，因此一个方案的量子比特容量越大，制备成本就越低，也就越实用.

本文方案的另一个特点是，制备和测量全部由Alice来完成，所有Bob仅需进行本地的酉操作即可.因此，本文方案对接收方的设备要求较低，特别适用于Alice的设备条件远远超过所有Bob的情况.

4 结语

本文提出了一种基于六量子态的高容量QSS方案.在该方案中，发送方Alice首先制备一串态为的单光子，根据要共享的秘密进行特定的酉操作以及一次随机的酉操作，然后将光子序列发送给Bob 1.所有Bob依次进行随机酉操作后，由Bob n将光子序列返回给Alice.Alice根据Bob提供的信息，使用正确的测量基对光子进行测量，并公布与测量结果有关的信息.所有Bob通过该信息和各自的酉操作即可获得要共享的秘密.本文方案可抵御常见的不可见光子、特洛伊木马、截获-重发、篡改、谎报等攻击，具有较好的安全性.理论分析结果表明，该方案的量子比特容量比已有的类似方案高，因此所需量子资源相对较少，实现代价较低.另外，本文方案中接收方所需的操作较简单，特别适用于发送方设备条件远超过接收方的情况.

References)

［1］Bennett C H，Brassard G.Quantum cryptography:public key distribution and coin tossing［C］//Proceedings of IEEE International Conference on Computers，Systems and Signal Processing.Bangalore，India，1984:175-179.

［2］Karlsson A，Koashi M，Imoto N.Quantum entanglement for secret sharing and secret splitting［J］.Physical Review A，1999，59(1):162-168.

［3］Guo G，Guo G.Quantum secret sharing without entanglement［J］.Physics Letters A，2003，310(4):247-251.

［4］Yan F L，Gao T.Quantum secret sharing between multiparty and multiparty without entanglement［J］.Physical Review A，2005，72(1):012304.

［5］Gao T，Yan F L，Li Y C.Quantum secret sharing between m-party and n-party with six states［J］.Science in China Series G，2009，52(8):1191-1202.

［6］Xu J，Chen H，Liu W，et al.An efficient quantum secret sharing scheme based on orthogonal product states［C］//Proceeding of 2010 IEEE Congress on Evolutionary Computation.Barcelona，Spain，2010:949-952.

［7］Shi R H，Huang L S，Yang W，et al.Asymmetric multi-party quantum state sharing of an arbitrary m-qubit state［J］.Quantum Information Processing，2011，10(1):53-61.

［8］Liu Z H，Chen H W，Xu J，et al.High-dimensional deterministic multiparty quantum secret sharing without unitary operations［J］.Quantum Information Processing，2012，11(6):1785-1795.

［9］Xu J，Chen H W，Liu Z H，et al.Quantum secret sharing without exclusive OR of qubits'measuring results［C］//Proceedings of 2012 IEEE Congress on Evolutionary Computation.Brisbane，Australia，2012:613-616.

［10］Xu J，Yuan J B.Improvement and extension of quantum secret sharing using orthogonal product states［J］.International Journal of Quantum Information，2014，12(1):1450008.

［11］Wagenknecht C，Li C M，Reingruber A，et al.Experimentaldemonstration ofa heralded entanglement source［J］.Nature Photonics，2010，4:549-552.

［12］Shor P W，Preskill J.Simple proof of security of the BB84 quantum key distribution protocol［J］.Physical Review Letters，2000，85(2):441-444.

［13］Cai Q.Eavesdropping on the two-way quantum communication protocols with invisible photons［J］.Physics Letters A，2006，351(1):23-25.

［14］Deng F G，Li X H，Zhou H Y，et al.Erratum:improving the security of multiparty quantum secret sharing against Trojan Horse attack(Phys.Rev.A 72，044302(2005))［J］.Physical Review A，2006，73(4):049901.

［15］Li C M，Chang C C，Hwang T.Comment on“quantum secret sharing between multiparty and multiparty without entanglement”［J］.Physical Review A，2006，73(1):016301.