求解物理方程
——Matlab软件在物理教学中的应用之一
2014-06-28朱国强
朱国强
(绍兴市第一中学 浙江 绍兴 312000)
在1859年,中国清代数学家李善兰开始将英文“equation”——指含有未知数的等式——一词翻译为“方程”.
方程按照学术程度可以分为初等数学方程和高等数学方程.方程按照解的形式可以分为数值方程和符号方程.方程按照学科分类可以分为代数方程、几何方程、三角方程、反三角方程、逻辑方程、微分方程、积分方程等.例如中学生熟悉的初等数学领域的代数学中的方程,可称为初等代数方程,包括整式、分式方程,一元、多元方程,有理式、无理式方程等.
两个或两个以上的方程的组合叫做方程组.解方程组包括数值方程组运算和符号方程组运算.Matlab不仅仅以数值运算见长,而且使用了Maple的内核,符号运算也极其厉害.见识过Matlab解符号方程组后,许多中学生深感惊奇.
1 符号变量和表达式
(1)定义符号变量
Matlab提供了函数syms,一次可以定义多个符号变量.其一般格式为:syms arg1 arg2 …argn.
(2)符号表达式
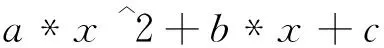
2 Solve函数及用法
Matlab内置Solve函数提供了初等数学方程的求解方案.Solve函数隶属于符号数学工具箱(Symbolic Math Toolbox).其用法为:
g = solve(eq)
g = solve(eq,var)
g = solve(eq1,eq2,..., ,eqn)
g = solve(eq1,eq2,...,eqn,var1,var2,...,varn)
其中,eqn为第n个方程的符号表达式,varn为第n个变量.
2.1 求解数值方程
应用Solve函数解方程通常给出的是解析解.想要获得方程的数值解,有多种方法.第一种是应用subs函数,subs函数用于替换求值.第二种是应用eval函数,计算一个表达式的值.分别举例说明.
(1)Solve求出解析解,subs求出数值解
Subs函数的常见格式为R = subs(S) ,用调用函数的值或者Matlab工作空间中的值来替代符号表达式S中出现的所有变量.
R = subs(S, new),用new来代替表达式S中的默认变量;
R = subs(S,old,new) ,用new符号变量或数值或表达式来替代来符号表达式S中old符号变量或字符串表达式.
【例1】质量为m=1 kg的金属块放在水平桌面上,在与水平方向斜向上成θ=37°,大小为F=10 N的拉力作用下,向右做直线运动.已知金属块与桌面间的动摩擦因数为μ=0.5.重力加速度g=10 m/s2.求金属块的加速度大小.
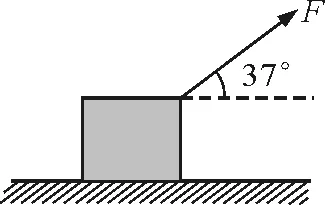
图1
解析:该题属于应用牛顿运动定律解决问题中的已知受力情况求运动情况的类型.主要方程为
Fcosθ-f=ma
Fsinθ+N-mg=0
f=μN
第一步,建立模型,列方程组,求出解析解.
输入≫syms F f N miu thita m g a;
S=solve(′F*cos(thita)-f=m*a′,′F*sin(thita)+N=m*g′,′f=miu*N′,′a′,′f′,′N′);
a=simple(S.a)
解得a =(F*cos(thita)+miu*F*sin(thita)-miu*m*g)/m,其中simple函数用来简化表达式.
即Matlab解得
第二步,根据题意,代入数据,得到数值解.
F=10;miu=0.5;thita=37*pi/180;g=10;
m=1;
a=subs(a)
解得a=5.995 4,即加速度大小为5.995 4 m/s2.
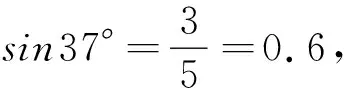
(2)Solve求出解析解,eval求出数值解
【例2】(2013年高考江苏卷第13题)
如图2所示,匀强磁场中有一矩形闭合线圈abcd,线圈平面与磁场垂直. 已知线圈的匝数N=100,边长ab=1.0 m,bc=0.5 m,电阻r=2 Ω. 磁感应强度B在0~1 s内从零均匀变化到0.2 T.在1~5 s内从0.2 T均匀变化到-0.2 T,取垂直纸面向里为磁场的正方向.求:
(ⅰ)0.5 s时线圈内感应电动势的大小E;
(ⅱ)在1~5 s内通过线圈的电荷量q;
(ⅲ)在0~5 s内线圈产生的焦耳热Q.
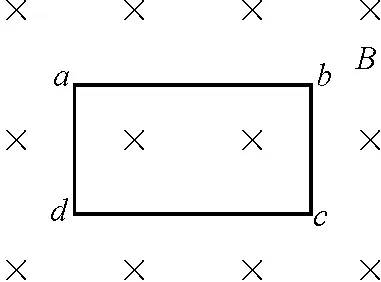
图2
解析:
该题知识点为法拉第电磁感应定律
电荷量
焦耳热
Q=I2Rt
第一步,根据题意,建立变量,并赋数值.
syms L1 L2 r N t1 t2 t3 B0 B1 B2 E q Q
L1=1;L2=0.5;r=2;N=100;B0=0;B1=
0.2;B2=-0.2;t1=0.5;t2=1;t3=5;
第二步,建立模型,列方程组,求解方程.
A=solve(′E=N*(B1-B0)*L1*L2/(t2-0)′,′q=N*(B1-B2)*L1*L2/r′,′Q=(N*(B1-
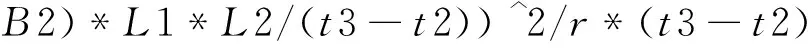
E=eval(A.E)
q=eval(A.q)
Q=eval(A.Q)
解得E=10;q=10;Q=100.000 0.即感应电动势的大小E=10 V ,电荷量q=10 C ,焦耳热Q=100 J.
2.2 求解符号方程
基本方法是solve(eq1,eq2,…,eqn,v1,v2,…,vn),即求解由表达式eq1,eq2,…,eqn组成的方程组,求解变量分别为v1,v2,…,vn.
【例3】(2008年高考全国Ⅰ卷第23题)
已知O,A,B,C为同一直线上的4点,AB间的距离为L1,BC间的距离为L2,一物体自O点静止起出发,沿此直线做匀加速运动,依次经过A,B,C三点.已知物体通过AB段与通过BC段所用时间相等,求O与A的距离.
解法一:(人工求解)
设物体加速度为a,经过OA段时间为t,经过AB段和BC段的时间均为T,O与A间的距离为x.
对物体,OA段
(1)
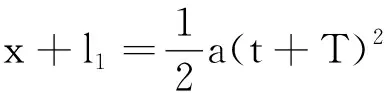
(2)
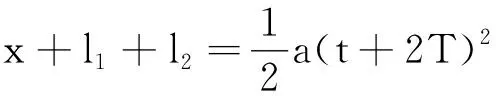
(3)
联立式(1)~(3),解得
解法二:(计算机求解)
输入syms x a t T L1 L2 v1;
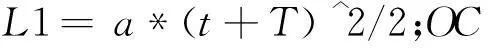
A.x
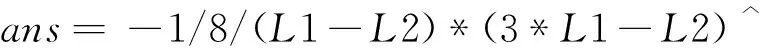
本题属于方程个数少于未知数个数的情形,有5种以上的解法.教学实践表明,一些学生列出方程组、求解,需要相当长的时间,有一定的难度,而用Matlab求解则无此困难.
通过以上例子可以看出,用Matlab解各类初等数学方程组是非常方便的,只要注意正确书写参数就可以了.
3 求解高等数学方程
高中物理教师在教研或者指导学生竞赛,需要用到高等数学来分析解决问题.一般常用的有积分、微分运算,求解微分方程等.Matlab对问题的描述和求解符合人们的思维方式和数学表达习惯,可以快速地求解高等数学方程.
3.1 积分函数int
函数int的用法为S=int (y,v,a,b),其中y是被积函数,v是积分变量,a与b积分下、上限.不定积分的输出结果是符号表达式,定积分的输出结果是符号表达式或数值.
【例4】计算纯电阻电路中正弦交流电i=Imsinωt在一个周期内的平均功率和电流的有效值.电阻R已知.
解析:
瞬时功率p=i2R=Im2Rsin2ωt,一个周期内的平均功率
运用Matlab求解的程序如下:
syms Im omiga t R I
i=Im*sin(omiga*t);
(2*pi/omiga)
解得
即
又将p代入
I=simple(I)
解得
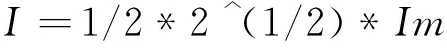
即有效值
3.2 dsolve函数解常微分方程
dsolve函数用法:S = dsolve(eqn,cond),用初始或边界条件cond求解常微分方程eqn.
【例5】如图3所示,平行导轨上放置一金属杆AB,质量为m,长为L,在导轨的上端接有电阻R.匀强磁场B垂直导轨平面向里.当AB杆以初速度v0向运动时,求:
(1)AB杆能够移动的距离;
(2)在移动过程中电阻R上放出的焦耳热.
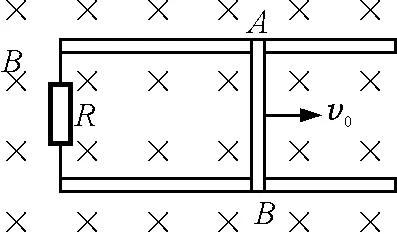
图3
解析:
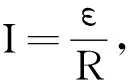
输入≫syms v t B L R m v0
解得
即方程的特解为
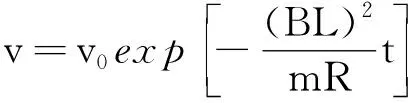
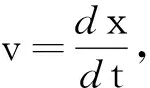
输入≫syms v t B L R m v0 x
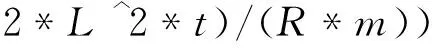
x=simple(x)
解得
即方程的特解为
当时间t→∞时,杆移动距离为
(2)杆在移动过程中产生的焦耳热元为
整个运动过程中产生的焦耳热为
输入syms x v a B L m t v0 R
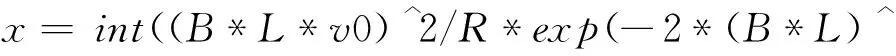
解得
【例6】如图4所示,一个矩形的金属线框,边长分别为a和b(b足够长).金属线框的质量为m,自感系数为L,忽略电阻.线框的长边与x轴平行,它以速度v0沿x轴的方向从磁场外进入磁感应强度为B0的均匀磁场中,B0的方向垂直矩形线框平面.求矩形线框在磁场中速度与时间的关系式v=v(t)和沿x轴方向移动的距离与时间的关系式x=x(t).
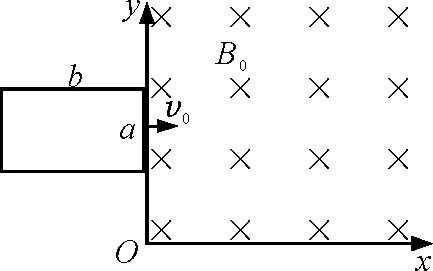
图4
解析:
由于b边很长,所以线框只有右边框切割磁感线,当线框速度为v时,产生的动生电动势ε=B0av;当线框中的电流为i时,产生的自感电动势的大小为
根据欧姆定律得
ε+εL=iR
由于不计电阻,所以有
(4)
右边框受力F=iaB0,根据牛顿第二定律,得
求导得
(5)
联立式(4)、(5)得微分方程
初始条件当t=0时,v=v0,a=0.
输入>>syms x v a B0 L m t v0
解得
即速度方程为
又由于
所以
初始条件t=0时,x=0.
输入syms x v a B0 L m t v0
(1/2)*t),t)
解得
即位移方程为
参考文献
1 黄忠霖,黄京.Matlab 符号运算及其应用.北京:国防工业出版社,2004
2 朱国强.应用Matlab求解物理方程.中国教育信息化,2012(3)
3 朱国强.高中物理培优基础教程(第二版).杭州:浙江大学出版社,2012,318~319,441~442
