斜拉索轴向激励作用下的面内参数振动

孙群涛

（湖南交通职业技术学院，湖南长沙 410132）

斜拉索是斜拉桥的主要承重部件，因其具有柔性大、阻尼小的特点，当桥面在风、车辆及地震等作用振动时，若桥面的振动频率与某一拉索的固有频率成倍数，微小的桥面振动即可引起拉索的大幅振动［1］。在工程中，由拉索大幅振动造成的工程事故也频频发生。1996年4月，荷兰的Erasmus大桥通车仅一个多月，就因索的大幅振动被迫关闭；在1994～1995年南浦大桥曾3次因拉索的振动而导致减振器的脱落。因此，参数振动问题已引起有关学者的高度重视，他们对参数振动的机理和控制方法进行了广泛的研究，并取得了许多具有工程价值的研究成果。Fujino［2］建立了索－桥耦合2自由度振动模型。亢战［3］建立了索－桥耦合2自由度振动模型，且运用多尺度法，得到了拉索的主参数共振。分析结果表明：拉索与桥面的振幅此消彼长，且拉索的振幅远大于其初值，而桥面的振幅与其初值接近。汪至刚［4－5］取拉索的一阶振动模态进行了分析，计算了拉索的主共振和参数共振情况，并提出了在拉索根部安装被动质量阻尼器的减振方法。赵跃宇［6］建立了小垂度斜拉索在端部轴向正弦激励下的振动模型，考虑拉索的一阶振动模态，分析了3种情况（激励与拉索频率比分别为1∶1，1∶2及2∶1）下的振动。陈水生［7］等人对拉索轴向激励下的面内参数振动进行了分析，得到了使拉索产生参数共振的最小激励幅值，并对瞬态与稳态索的内力变化进行了分析。赵跃宇［8］等人采用斜拉索受轴向激励的力学模型，用多尺度法，对拉索稳态运动的稳定进行了分析。

作者拟根据拉索轴向激励下的模型并运用哈密顿变分原理，求解拉索的参数振动方程。不同于大部分学者所利用经典的牛顿运动定律的微分方法。该方法是以积分方程来由局部求整体的，通过求解系统作用量的平稳值，更准确地表达了系统对于任何微扰随时间的演变，具有较强的时间、空间连续性。采用变分法，计算整个系统的运动方程。采用多尺度法，对系统的运动方程进行分析。采用标准四阶龙格—库塔数值方法，求解运动方程。并用MATLAB编程，进行参数分析，分析影响拉索参数振动的因素频率比、激励振幅、拉索阻尼比及索力对斜拉索主共振和参数振动的影响。

1 建立拉索面内参数振动方程

为方便研究且能体现问题本质，假设：①忽略垂度对拉索质量重分布的影响，认为斜拉索的垂度曲线为抛物线；②忽略拉索的抗弯刚度、抗扭刚度及抗剪刚度；③不考虑材料非线性，变形本构关系服从胡克定律，且各点受力均匀；④不计桥面和桥塔对拉索的影响；⑤拉索只发生面内振动。

建立如图1所示的坐标系，拉索的静态线形为y（x）。拉索振动时，x和y方向离开静平衡位置的位移分别为u（x，t）和v（x，t），拉索轴向位移激励

图1 轴向激励下斜拉索面内振动模型Fig.1 Stayed－cable in－plane vibration model caused by axial excitation

拉索单位索长质量、弹性模量、截面面积、初始曲线长度、初张力及阻尼系数分别为m，E，A，L，T0及μ，静态和动态弧长微段分别为ds和ds′，则

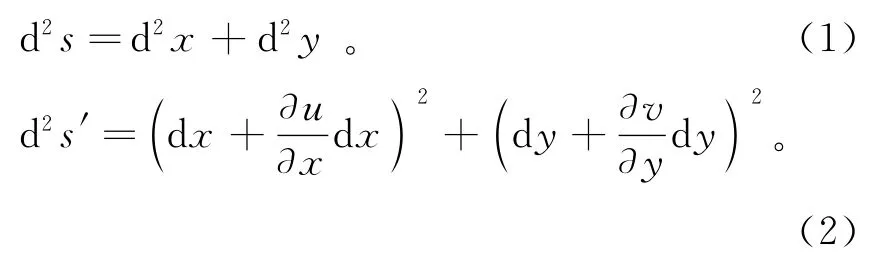
则拉索的动应变ε为：

拉索的动能和势能分别为：

运用Hamilton原理，有：

根据模型可知，时间边界条件为：

几何边界条件为：

静力平衡条件为：

根据式（7）～（9），分别计算T和V的变分，得：

将式（10）和式（11）代入式（6），得：

根据已知边界条件可知，索的动应变只与时间有关，由于纵向振动相对于横向振动较小，因此，忽略二阶小量近似认为ds≈dx，得到动应变：

由图1可知，本模型位移边界条件为：

对式（13）进行积分，并根据边界条件，得：

由于拉索接近张紧弦，近似取索的振动模态为标准弦的模态。根据Tagata实验，张紧弦的端激励振动中，基本模态占主要地位，故进行一阶模态截断，即

根据静力平衡条件，得：

将式（16），（17）及（18）代入式（12），并近似认为ds≈dx，得：

运用Galerkin方法，进行方程解耦。在方程两边同时乘以在［0，L］区间内进行积分，得：

式中：2ξ1ω1＝μ／m；ξ1为拉索的阻尼比；ω1为考虑综合效应后的一阶固有频率（2／π）4／2）；λ2为索的垂度系数，λ2＝4EABL2／T；ω0为不考虑垂度影响的一阶固有频率，

2 多尺度法求解

为方便研究，引入无量纲小参数ε，将方程（20）改写为：

式中：ε2χ1＝－2ξ1ω1；ε2f＝－a；εg＝－d。

引入不同尺度时间变量：

本研究只讨论二次近似解，令

展开后，令ε的同次幂系数为零，得到各阶近似的线性偏微分方程。

ε阶：

ε2阶：

ε3阶：

方程（24）的解可写为负数形式：

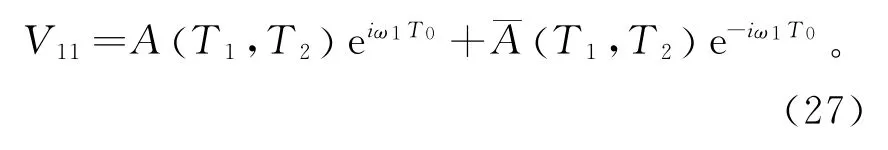
将（27）代入（25），得：

为了保证有周期解，需要消除久期项，得：

2.1 非内共振情况

将式（27）和式（30）代入（26），得：

消除式（31）久期项，得：

2.2 内共振情况

将式（34）代入方程（31）并消去久期项，得：

将复函数A写为指数形式，得：

式中：α（t）和θ（t）的解为t的实函数。代入式（35），分离实部、虚部，并令γ＝ε2σT0－θ，得：

方程组（37），（38）的非零常值特解αs和γs对应于系统的稳态周期运动。令导出αs和γs应满足的条件：

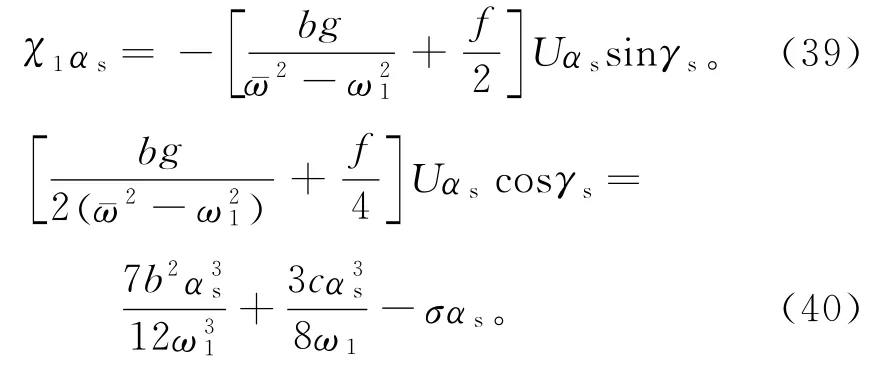
消去γs，得：

由式（41）移项，得：

可见，振幅αs有稳态解的条件是此时系统产生持续不断的运动。在满足αs有稳态解的条件下，如果则αs有一个稳态解；如果则αs存在两个稳态解。

为判断振动的稳定性，引入扰动变量ξ＝ααs，η＝γ－γs，得到在奇点（αs，γs）附近的一次近似方程：

该线性扰动方程为：

3 参数分析

本研究以涪丰石高速乌江特大桥拉索FDB19为例进行分析，拉索参数为：m＝72.8kg／m；T0＝5 352.2kN；A＝9 270.065×10－6m2；θ＝32.732°；L＝179.412m；f＝0.750 1Hz；E＝1.95×105MPa。

采用标准四阶龙格—库塔法［7］，求解式（20）。为方便计算，在计算过程中，进行了参数修改，分析不同情况下拉索的振动。运用MATLAB，进行编程［8］。

假定索的初始扰动V1（0）＝10－4m，激励幅值U（0）＝0.1m，暂不考虑阻尼的影响，作出激励频率与拉索频率在［0.1，3］内拉索的跨中振幅变化曲线，如图（2）所示，其中ωr＝

图2 斜拉索跨中振幅与频率比关系曲线Fig.2 The curve between the cable－stayed span amplitude and the frequency ratio

图3 ／ω1＝1时，位移时程曲线Fig.3 The displacement versus time when／ω1＝1

图4 ／ω1＝2时，位移时程曲线Fig.4 The displacement versus time whenω－／ω1＝2

图5 斜拉索跨中响应幅值与激励幅值的关系曲线Fig.5 The curve between the cable－stayed span amplitude and the excitation amplitude

从图5中可以看出，拉索的跨中响应随激励幅值的增大而增大，呈非线性增大关系。随着激励幅值的增大，拉索在参数振动下的最大响应幅值将大于主共振最大幅值。当激励幅值较小时，主共振为影响较大。当激励幅值较大时，参数共振的影响将超过主共振，必须引起高度重视。

从图6，7中可以看出，斜拉索阻尼比与跨中振幅整体呈非线性递减关系。当时，在一定范围内，阻尼比的增大对减振作用显著。随着阻尼的增大，振幅减小缓慢。当且阻尼比达到某一数值时，将会引起跨中响应振幅的急剧下降。当激励振幅较小时，小阻尼即可引起拉索跨中响应振幅的急速下降，激励幅值越大，引起拉索跨中响应振幅骤降的阻尼比越大。当跨中响应振幅减小到某一数值之后，跨中响应振幅与阻尼比接近线性关系，且衰减缓慢。

图6 ω－／ω1≈1时，斜拉索跨中振幅与阻尼比关系曲线Fig.6 The curve between the cable－stayed span amplitude and the damping ratio when／ω1≈1

图7 ω－／ω1≈2时斜拉索跨中振幅与阻尼比关系曲线Fig.7 The curve between the cable－stayed span amplitude and the damping ratio when／ω1≈2

拉索跨中最大振幅与索力关系曲线如图8所示。从图8中可以看出，无论是主共振还是参数共振，拉索跨中最大响应振幅都随索力的增大而减小。当索力达到某一数值之后，索力变化对参数振动的最大响应振幅影响将减小。

图8 拉索跨中最大振幅与索力关系曲线Fig.8 The curve between the cable－stayed maximum span amplitude and the cable tension

4 结论

2）拉索的振动出现“拍”现象，且由于垂度效应拉索振动的正、负振幅不对称。在文献［3～5，9］中，用牛顿定律建立的方程得到了相同结论。

3）拉索振动的振幅与激励振幅呈非线性增大关系，因此控制激励振幅可以有效地控制拉索振动。在文献［3，5，7，9］中，用牛顿定律建立的方程得到了相同结论。

4）拉索的阻尼比与跨中振幅呈非线性递减关系，则控制拉索的阻尼比可以有效地控制拉索的振动，但当阻尼比达到一定值之后，再增大阻尼比的意义不大。

5）拉索的索力与跨中振幅呈非线性递减关系。这说明增大索力可以控制拉索的振动，特别是主共振，但是索力还需结合其他条件确定。

（References）：

［1］Costa A，Martinsjac，Brancof，et al.Oscillations of bridge stay cables induced by periodicmotions of decks and towers［J］.Journal of Engineering Mechanics，1996（7）：613－621.

［2］Fujino Y P.Warnitchai，B.M.Pacheco.An experimental and analytical study of autoparametric resonance in a 3DOF model of the cable－stayed beam［J］.Nonlinear Dynamics，1993，（4）：111－138.

［3］亢战，钟万勰.斜拉桥参数共振问题的数值研究［J］.土木工程学报，1998，31（4）：14－22.（KANG Zhan，ZHONG Wan－xie.Numerical study on parametric resonance of the cable－stayed bridge［J］.China Civil Engineering Journal，1998，31（4）：14－22.（in Chinese））

［4］汪至刚.大跨度斜拉桥拉索的参数振动与控制［D］.杭州：浙江大学，2000.（WANG Zhi－gang.Parametric vibration and control of long span cable－stayed bridges［D］.Hangzhou：Zhejiang University，2000.（in Chinese））

［5］汪至刚，孙炳楠.斜拉索的参数振动［J］.土木工程学报，2002，35（5）：28－33.（WANG Zhi－gang.SUN Bing－nan.The parametric vibration of stayed cables［J］.China Civil Engineering Journal，2002，35（5）：28－33.（in Chinese））

［6］赵跃宇.大跨径斜拉桥非线性动力学的模型与理论研究［D］.长沙：湖南大学，2000.（ZHAO Yue－yu.Model and theoretical study on nonlinear dynamics of long span cable－stayed bridge［D］.Changsha：Hunan University，2000.（in Chinese））

［7］陈水生，孙炳楠.斜拉桥索－桥耦合非线性参数振动数值研究［J］.土木工程学报，2003，36（4）：70－75.（CHEN Shui－sheng，SUN Bing－nan.Numerical study on nonlinear parametric vibration of coupled cables and bridge decks［J］.China Civil Engineering Journal，2003，36（4）：70－75.（in Chinese））

［8］赵跃宇，王涛，康厚军.斜拉索主参数共振的稳定性分析［J］.动力学与控制学报，2008，6（2）：112－117.（ZHAO Yue－yu，WANG Tao，KANG Hou－jun.Stability analysis of the cable principal parametric resonance［J］.Journal of Dynamics and Control，2008，6（2）：112－117.（in Chinese））

［9］李凤臣，田石柱，欧进萍.大跨度斜拉桥拉索的参数振动［J］.沈阳建筑大学学报，2008，24（5）：737－742.（LI Feng－chen，TIAN Shi－zhu，OU Jin－ping，Parametric vibration of cables of the cable－stayed bridge［J］.Journal of Shenyang Jianzhu University，2008，24（5）：737－742.（in Chinese））