三维球、柱坐标系下导热微分方程的离散求解

贾欣鑫，徐明海，胡国华，刘娟，路辉，梁卓

三维球、柱坐标系下导热微分方程的离散求解

贾欣鑫，徐明海，胡国华，刘娟，路辉，梁卓

(中国石油大学(华东)储运与建筑工程学院，山东青岛266555)

根据柱坐标系与球坐标系的导热微分方程式推出了导热微分方程在球坐标系、柱坐标系上的三维高精度数值求解离散公式，并与解析解进行对比，验证了该离散公式有较高的精确度。在球坐标系下离散θ扩散项时，运用积分第一中值定理成功处理了复杂的θ扩散项的离散系数。该离散格式为三维柱坐标与球坐标下导热微分方程的数值求解提供了良好的借鉴作用。同时为导热微分方程在工程计算中的应用提供了精确的数值离散格式与理论依据。

导热微分方程;球坐标系;数值传热;积分第一中值定理

数值传热学在解决实际复杂传热问题中得到广泛的应用［1－3］，其对应的导热偏微分方程的离散一直都是解决数值传热问题的关键之一。在数值传热学中，二维柱坐标与极坐标导热微分方程已得到了较好的推广应用。目前在离散与解决三维柱坐标与球坐标时，缺少较为明确的数值求解的离散格式［4－5］。现今数值传热学对于柱体与球体的数值求解，只是通过简化为径向或者二维极坐标的方式来解决，这给数值传热学在三维柱坐标与球坐标条件下的计算、推广与应用造成了诸多不便，因此合理准确地得到三维圆柱体导热、球体导热偏微分方程显得尤为重要。基于以上考虑本文以三维柱坐标与球坐标为基础，从微分方程的数值解离散格式方面入手，推导出精度较高的柱坐标与球坐标导热微分方程离散格式，并通过一维解析解对比验证其精确度。

1 导热偏微分方程的提出

将导热微元体置于直角坐标系中，运用能量守恒原理和傅里叶(Fourier)定律［6］，建立直角坐标系下导热微分方程

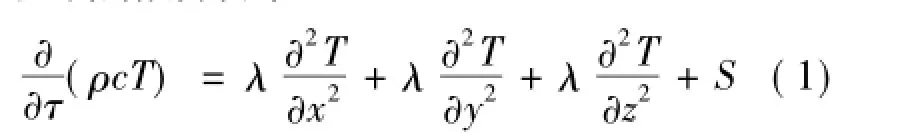
其中:λ为导热系数;c为导热体热容;S为内热源强度。

采用坐标变换法分别得到圆柱坐标系与球坐标系中导热微分方程

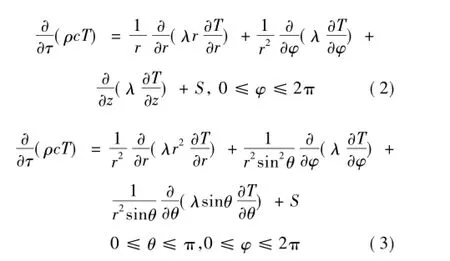
离散导热微分方程离散的基本方法主要有2种:Taylor级数展开法和有限体积法［7－8］。为明确其导热偏微分方程的物理概念及保证离散系数的意义，本文采用有限体积法，即控制容积法。

2 柱坐标系下导热微分方程的离散

首先给方程(2)两边同时乘以r，然后对偏微分方程两边同时在图1所示的控制容积以及非稳态的时间项中积分:

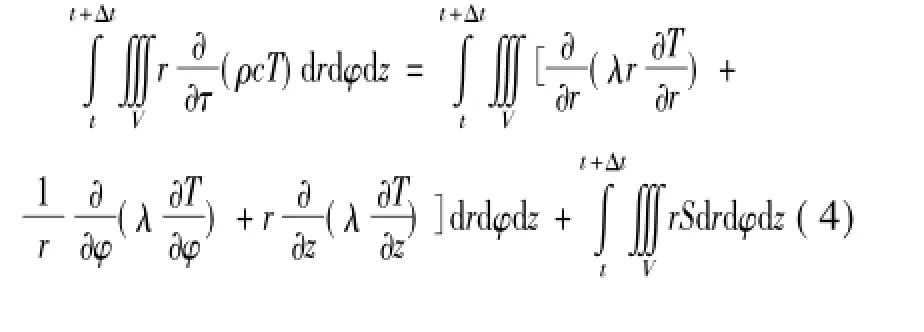
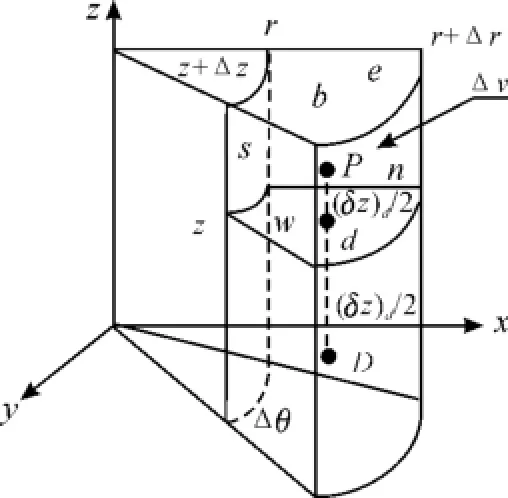
图1 圆柱体控制容积

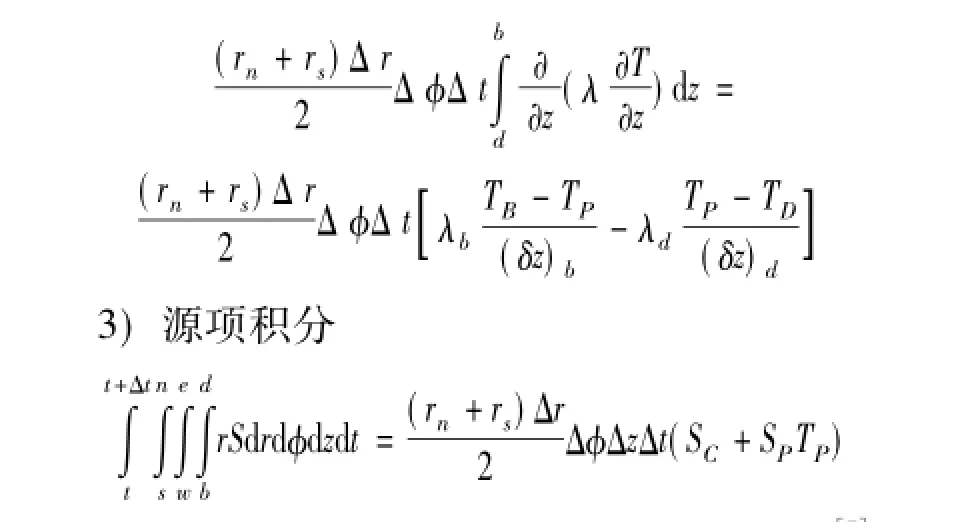
其中:源项中S表示成为未知量的线性函数［7］;SC为常数部分;SP表示S随温度T变化而变化的曲线在P点的斜率。

4)离散结果

整理以上结果可得:

3 球坐标系下导热微分方程的离散

对控制方程(3)两边同时乘以r2sin2θ，对导热微分方程在图2所示的控制容积在非稳态时间项中积分得:

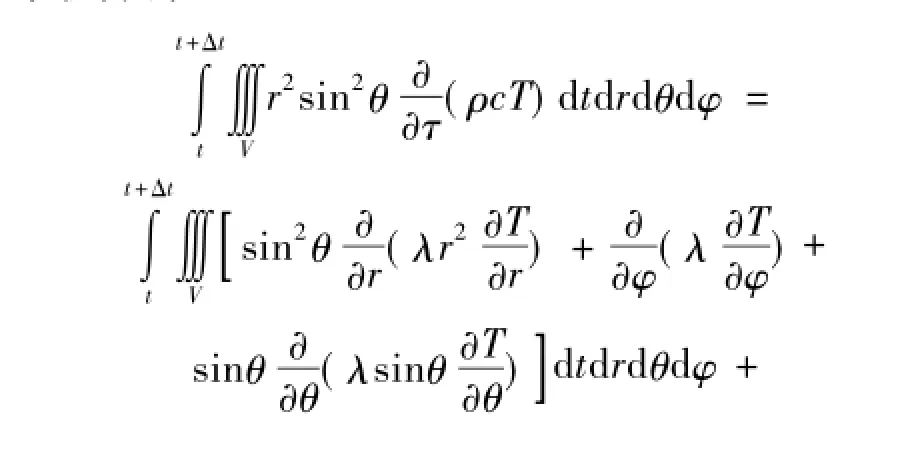
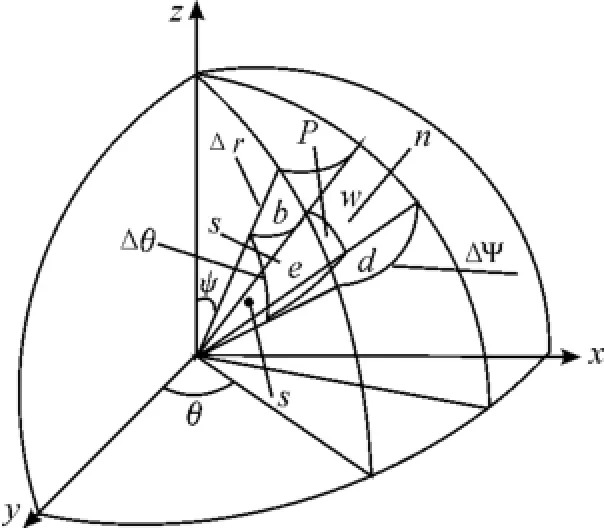
图2 球体控制容积

4 实例验证

4.1 圆柱体导热离散方程的验证及网格无关性分析

为验证其离散解数值解的准确性，考察一个内外径分别为R1、R2的圆筒壁，圆筒的内外两侧保持无量纲温度T1、T2，其径向导热解析解为

应用本文离散方程，得到如图3所示高精确度的数值解，误差为8.86×10－3%。

图3 圆柱体解析解与数值解

通过增加计算区域网格的的数目，计算其误差的大小，进行网格无关性的分析，误差的计算方式为

式(9)中:error表示误差;T表示解析解;Tnum表示本文数值解。

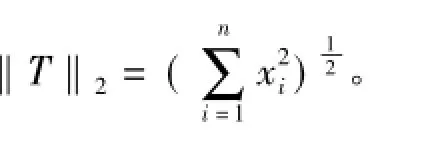
根据误差分析网格无关解［11－12］得到如图4所示的误差与网格数的关系。通过数值计算得出:当网格数增加到5 000时，计算误差已经控制在1%以内，随着网格的加密计算误差逐渐减少。本文的解析解误差为8.86×10－3%，选用计算网格数为37×20×16=11 840。

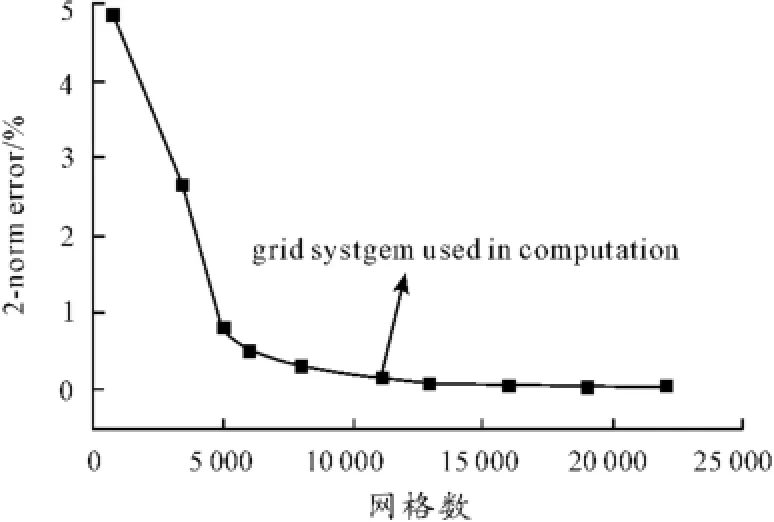
图4 圆柱体网格数与误差关系

4.2 球体导热离散方程的验证

为验证其球壳离散解数值解的准确性，选取内外径分别为R1、R2的球壳，球壳的内外两侧保持恒温T1、T2，验证其一维径向导热问题。解析解为

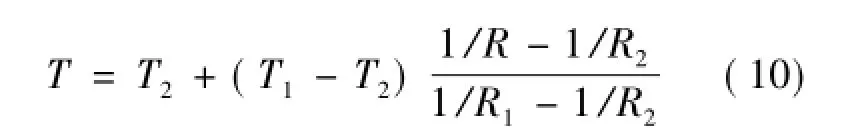
无热源稳态导热圆柱边界条件:

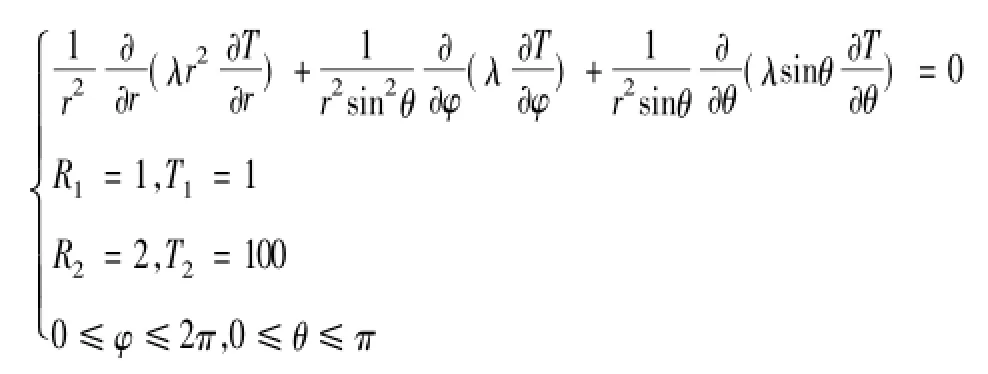
应用本文离散方程，得到如图5所示的数值解，误差为0.53%。

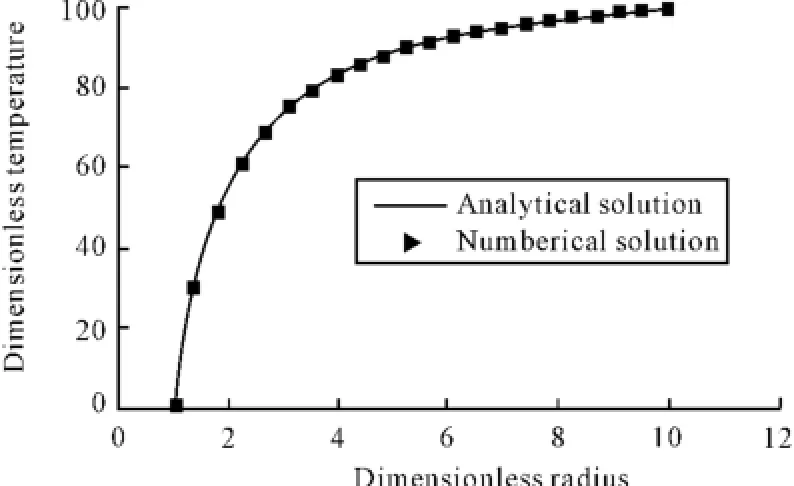
图5 球体解析解与数值解

图6为误差与网格数的关系。通过图6可以看出:当网格数增加到12 000时，计算误差已经控制在0.5%以内，随着网格的加密计算误差逐渐减小。本文的解析解误差为0.53%，选用网格数为47×20×12=11 280。

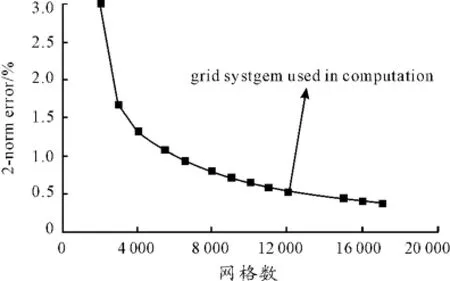
图6 球体网格数与误差关系

5 结束语

研究了圆柱体与球体的三维导热微分方程，对其进行有限容积法的高精度的数值计算离散格式推导。在离散球体的过程中，运用积分第一中值定理从理论上处理了复杂θ扩散项的离散系数。该离散格式为科研工作者进行三维柱坐标与球坐标下导热微分方程的数值求解提供了良好的借鉴。该离散格式的验证应用FORTRAN语言编写计算，运行稳定，在理论基础上验证了解析解与数值解的误差，将球体的误差范围控制在了0.5%以内，为三维柱体与球体导热偏微分方程的研究与工程应用提供了高精度、可靠的数值计算离散格式。

［1］陶文铨.数值传热学［M］.2版.西安:西安交通大学出版社，2001.

［2］王辉，徐明海.边界界面导热系数插值格式的改进［J］.燕山大学学报:自然科学版，2010，34(5):411－417.

［3］黄善波，李兆敏.幂律流体同心环空内层流脉动流的数值分析［J］.中国石油大学学报:自然科学版，2011，35(2):127－136.

［4］金有海，姬广勤，曹晴云，等.旋风分离器排气管内气相流场的数值模拟［J］.中国石油大学学报:自然科学版，2008，32(6):109－112.

［5］DING P，WU XH，HE YL，et al.A fast and efficient method for predicting fluid flow and heat transfer problems［J］.ASM E Journal of H eat Transfer，2008，130:1－17.

［6］邓先琛.对建立球面坐标系中的导热微分方程式探讨［J］.安徽工学院学报，1987，6(4):58－70.

［7］PATANKA S V，SPALDING D B.A calculation procedure for heat，mass and momentum transfer in three－dimensional parabolic flow［J］.International Journal Heat Mass Transfer，1972，15:1787－1806.

［8］帕坦卡SV.传热与流动的数值计算［M］.张政，译.北京:科学出版社，1984:40.

［9］华东师范大学数学系编数学分析(上)北京:高等教育出版社，2001:218－219.

［10］同登科，周生田，吴爱弟，等.计算方法［M］.东营:石油大学出版社，2004:59－60.

［11］徐明海，张俨彬，陶文铨.一种改进的Delaunay三角形化剖分方法［J］.石油大学学报:自然科学版，2001，25 (2):100－105.

［12］LEE C K，HOBBSR E.Automatic adaptive finite element mesh generation over arbitrary two－dimensional domain using advancing front technique［J］.Computers＆Structure，1999，71:9－34.

(责任编辑 刘舸)

Numerical M ethod for Three-dimensional Heat Conduction in
Cylindrical and Spherical Coordinates

JIA Xin－xin，XU Ming－hai，HU Guo－hua，LIU Juan，LU Hui，LIANG Zhuo

(College of Pipeline and Civil Engineering，China University of Petroleum，Qingdao 266555，China)

According to the differential equations of heat conduction on cylindricaland spherical coordinate system，numerical solution of the discrete formulation on cylindrical and spherical coordinate system with high accuracy has been derived.Compared with the analytical solution，this discrete formula has been verified with a high degree of accuracy.Tomake the complex dispersion coefficient of diffusion termθmore concrete in spherical coordinates，this paper derived the discretion coefficientof diffusion termθby the firstmean value theorem of integral.The accurate schemes provides a good reference for researcherswhom work in solving the equation of heat conduction of three－dimensional cylindrical coordinates and spherical coordinates，and it will provide accurate numerical schemes and the theoretical basis for solving practical engineering problems.

differential equation of heat conduction;spherical coordinate;numerical heat transfer; the firstmean value theorem for integrals

TK121

A

1674－8425(2014)01－0033－05

10.3969/j.issn.1674－8425(z).2014.01.007