山东省人均用水量预测模型研究
——基于多元线性回归和BP神经网络模型
2014-06-27赵黎明赵岩
赵黎明,赵岩
(天津大学管理经济学部,天津 300072)
山东省人均用水量预测模型研究
——基于多元线性回归和BP神经网络模型
赵黎明,赵岩
(天津大学管理经济学部,天津 300072)
针对水资源供需矛盾日益严重的问题,采用多元线性回归模型和BP神经网络模型分别对人均用水量进行预测,并对两者预测结果进行比较,发现BP神经网络模型能更好地反映人均用水量及其因变量之间的复杂关系。结果表明:BP模型可有效解决人均用水量的预测问题,为政府部门进行相关预测和决策提供参考。
人均用水量;SPSS多元线性回归;BP神经网络;预测
水资源是当前经济社会发展的重要战略性资源,是制约区域经济可持续发展的重要因素。近年来,山东省国民经济快速发展,人民生活水平显著提高,对水资源的需求量越来越大,在山东省水资源总量有限的情况下,对用水量进行预测分析对制定未来水资源规划具有重要的现实意义。本文分别采用SPSS回归分析和BP神经网络对山东省人均用水量进行预测分析,以期找到一种精确、实用的用水量预测模型。
1 变量选择和数据收集
1.1 变量的选择
将影响人均用水量的因素分为两大类:经济水平和生活条件。前者用人均工农业产值、人均可支配收入来度量,后者用人均工业废水排放量、人均建筑面积和人均造林面积来度量。本文将采用生活条件这一因素对人均用水量进行预测。
以人均用水量Y(人/m3)作为被解释变量,以人均工业废水排放X1(人/t)、人均建筑面积X2(人/m2)、人均造林面积X3(人/m2)为解释变量建立多元回归模型。
1.2 数据的收集
建立包括人均用水量Y、人均工业废水排放X1、人均建筑面积X2、人均造林面积X3的数据库。根据《山东省统计年鉴(2012)》和《山东省水资源公报》搜集、整理模型的数据库,如表1所示。
2 多元线性回归分析
2.1 模型建立
运用SPSS18进行线性回归分析,相关数据如表2所示[1-3]。
通过表2可得,人均用水量的预测公式为


表1 山东省人均用水量预测原始数据(2000—2009年)
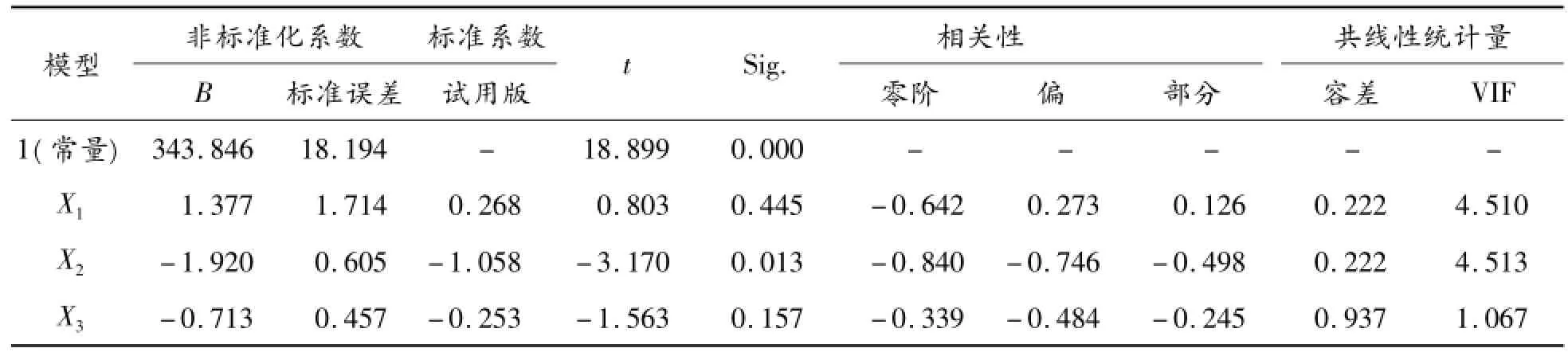
表2 线性回归系数
2.2 模型诊断
1)共线性检验
由表2可知:本模型的容忍度均大于0.01, VIF(方差膨胀系数)均小于10,此外特征值为3.899、0.087、0.02、0.004,只有一项略小于0.01,条件指标(CI)为1.000、6.684、13.947、30.215,只有一项略高于30。以上指标表明:本模型存在轻微的多重共线性问题。
2)拟合优度检验
根据回归分析,回归模型的样本决定系数R2=0.803,说明模型的3个自变量可以解释“人均用水量”因变量80.3%的变异量。根据R2检验规则,R2的值越接近1,代表方程的拟合优度越好,此处R2=0.803,表明人均用水量与人均工业废水排放量、人均建筑面积、人均造林面积的线性关系显著,回归模型能很好地反映实际数据的变化,方程的拟合优度较好。D-W=1.303,表明各残差项之间具有一定的正相关关系。
3)显著性检验
本例的F=10.849,显著性检验P值为0.003。本例取95%的置信区间(α=0.05),P= 0.003<α=0.05,表示回归模型整体解释变异量达到显著水平,由接近99.997%的概率可以断定,自变量对因变量产生显著的线性影响。
根据模型预测结果绘制人均用水量多元回归预测值与实际值比较图,如图1所示。根据相关数据预测2015、2020年的人均用水量为222.5 (人/m3)、225.7(人/m3)。
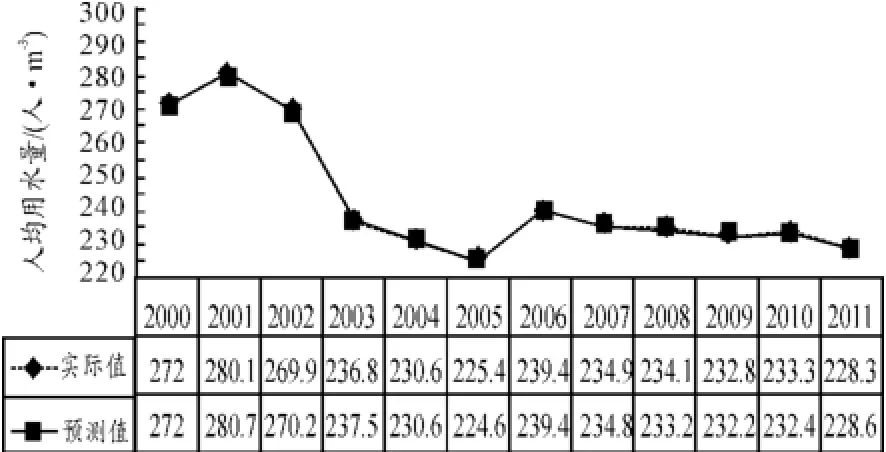
图1 人均用水量多元回归预测值与实际值的比较
3 BP神经网络分析
3.1 网络训练过程
1)归一化处理数据。使用SPSS18的转换功能,选择随机数字生成器,设置起点固定值为9 191 972,运用计算变量功能建立分区变量partition,数字表达式为2*rv.bernoulli(0.7)-1,将分区值设置为概率为0.7的Bernoulli变量。
2)将人均用水量Y选为因变量,人均工业废水排放X1(人/t)、人均建筑面积X2(人/m2)、人均造林面积X3(人/m2)为因子,使用分区变来那个partition来分区变量。
3)隐藏层数为一个,单位自动计算,激活函数Sigmoid,输出选择恒等函数,尺度因变量重标度选择标准化,修正值为0.02,培训类型为批处理,初始Lambda值、Sigma值为默认的0.000 000 5,0.000 05,间隔点中心数为0,间隔偏移量为±0.5。
根据模型预测结果绘制人均用水量BP预测值与实际值比较图[4-12],如图2所示;学习结果及残差数据见表3。根据相关数据预测2015、2020年的人均用水量为224.5(人/m3)、227.3(人/m3)。
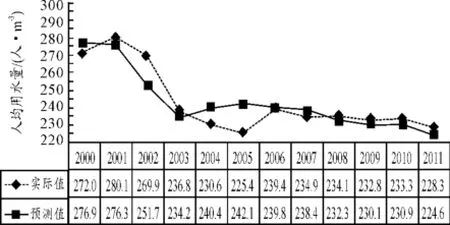
图2 人均用水量BP神经网络预测值与实际值的比较

图3 BP神经网络对因变量的观察预测图
3.2 结果检验
从BP神经网络关于因变量人均用水量的观察预测图可以看出:人均用水量Y的预测值基本位于从原点出发的45°线之上,模型的预测结果接近理想状况。此外,从表3可知:神经网络预测的最大残差为-0.92,最低预测精度为99.61%,表明模型具有较高的精确性。

表3 多元回归与BP神经网络预测结果比较
4 模型的比较
由图1、2及表3可知:BP神经网络对于人均用水量Y的预测较多元线性回归的预测更为敏感和精确,预测值的误差和精度都高于多元线性回归模型。本文分析这种现象的原因是两种模型本身的特点和此例因变量与自变量之间的关系共同决定的。
人均用水量Y与3个自变量之间并非典型的线性相关关系,同时自变量之间具有一定的相关关系,线性回归方程无法准确描述这种非线性相关关系和自变量的相关关系。BP神经网络模型属于隐含式的数学方法,在分析过程中不需要建立数学模型,只需要通过对原始数据训练得到稳定的学习网络,从而对数据进行预测,这种方法更加简便。因此,人均用水量Y与自变量的非完全的线性相关关系以及自变量之间的相关关系不会对神经网络预测产生影响,神经网络模型得以更好地模拟非线性方程。
5 结束语
人均用水量与相关自变量之间具有复杂的关系,BP神经网络的非线性映射功能可以很好地克服线性回归分析针对复杂关系变量时的不足。同时,BP神经网络操作方便,不需要人为地确定权重,降低了主观因素对预测造成的影响,预测结果更加精确。在人均用水量相关影响因素更加具体和精确以及神经网络自身不断完善的前提下,神经网络在人均用水量预测以及其他相关预测领域将得到更广泛的应用。
[1]Daily G C,Ehrlich P R.Socioeconomic equity,sustain-ability,and earth carrying capacity[J].Ecological Application,1996,6(4):991-1001.
[2]宇传华.SPSS统计分析[M].北京:电子工业出版社,2007.
[3]张红坡,张海锋.SPSS统计分析实用宝典[M].北京:清华大学出版社,2012.
[4]刘丹丹,冯利华,王宁,等.基于BP神经网络的义乌水资源需求量预测[J].水资源与水利工程学报,2010,21(4):114-117.
[5]王辉,孙世群,熊鸿斌.城市工业废水排放量灰色预测的研究[J].安徽化工,2005,(5):51-53.
[6]夏维力,吕晓强.基于BP神经网络的企业技术创新能力评价及应用研究[J].研究与发展管理,2005,17 (1):50-54.
[7]李永华,刘德,金龙.基于BP神经网络的汛期降水量预测模型研究[J].气象科学,2002,22(4):461-467.
[8]邓代强,朱永建,李健,等.基于BP神经网络的充填料浆流变参数预测分析[J].武汉理工大学学报,2012 (7):82-87.
[9]李连,孙聪,苏涛.基于蚁群改进BP算法的组合预测模型[J].四川兵工学报,2012(9):68-70.
[10]尹然,丁晓明,李小亮,等.基于SA-BP神经网络的软件缺陷预测模型的研究[J].西南师范大学学报:自然科学版,2013(8):147-152.
(责任编辑 刘舸)
[11]郭杰,欧名豪,刘琼,等.基于BP神经网络的南通市建设用地需求预测[J].资源科学,2009,31(8):1355-1361.
[12]刘树锋,陈俊合.基于神经网络理论的水资源承载力研究[J].资源科学,2007,29(1):99-105.
(责任编辑 刘舸)
Multivariate Linear Regression and BP Neural Network Model for Per Capita Water Consumption Forecasting Model Research in Shandong Province
ZHAO Li-ming,ZHAO Yan
(Economic Management Department,Tianjin University,Tianjin 300072,China)
Water resource is becoming one of the most important factors of economic and social development.In view of the problem of serious imbalance between supply and demand of water resources,
this paper used multivariate linear regression model and BP neural network model to forecast the per capita water consumption respectively,and made comparisons about the forecasting result.We found that the BP neural network model can better response the complicated relationship between the per capita water consumption and the dependent variable.BP model can effectively solve the problem of per capita water consumption prediction,and provide a reference for relevant prediction and decisionmaking for the government department.
per capita water consumption;SPSS multivariate linear regression;BP neural network; forecasting
TU991.5
A
1674-8425(2014)03-0131-04
10.3969/j.issn.1674-8425(z).2014.03.024
2013-11-22
赵黎明(1951—),男,河北人,教授,博士生导师,主要从事区域经济可持续发展(含旅游管理)、企业管理、市场研究等方面研究;通讯作者赵岩,硕士研究生,主要从事区域经济可持续发展专业研究。
赵黎明,赵岩.山东省人均用水量预测模型研究——基于多元线性回归和BP神经网络模型[J].重庆理工大学学报:自然科学版,2014(3):131-134.
format:ZHAO Li-ming,ZHAO Yan.Multivariate Linear Regression and BP Neural Network Model for Per Capita Water Consumption Forecasting Model Research in Shandong Province[J].Journal of Chongqing University of Technology:Natural Science,2014(3):131-134.
