基于Backstepping方法对超混沌Rossler系统的控制与同步研究

王 石，杨 吉，栾红霞

（1.东北师范大学信息化管理与规划办公室，吉林长春130024；2.空军航空大学基础部，吉林长春130022；

3.东北师范大学物理学院，吉林长春130024）

基于Backstepping方法对超混沌Rossler系统的控制与同步研究

王 石1，杨 吉2，栾红霞3

（1.东北师范大学信息化管理与规划办公室，吉林长春130024；2.空军航空大学基础部，吉林长春130022；

3.东北师范大学物理学院，吉林长春130024）

对超混沌Rossler系统提出了基于Backstepping的超混沌控制与同步方法，在反向递推每一步设计算法中构造虚拟控制器，使得构造的Lyapunov函数导数负定，逐步修正算法使误差系统在Lyapunov意义下渐近稳定，实现控制器的设计.只使用一个控制器实现了对超混沌Rossler系统控制与同步，数值实验结果证实了所设计控制器的有效性.

控制；同步；Backstepping方法；超混沌Rossler系统

混沌的控制与同步在生物医学、化学反应及保密通讯等领域应用受到了极大的关注，近些年来得到了蓬勃发展.人们提出了许多混沌控制与同步的方法［1－11］，Yassen等提出了利用Backstepping方法对严格反馈混沌系统实现混沌同步与控制，它是一种构造Lyapunov函数的系统方法，基于Lyapunov稳定性理论，将复杂系统分解成不超过系统阶数的子系统，在反向递推设计中构造虚拟控制器，逐步修正算法使误差系统在Lyapunov意义下渐近稳定，完成了控制器的设计［8－11］.以上设计主要针对一般混沌系统，而超混沌系统具有2个或2个以上正的Lyapunov指数，增大了系统的随机性和不可预测性，它在保密通信领域中具有更大的应用潜力，本文利用Backstepping方法只需要一个控制器实现对五阶超混沌Rossler系统的控制和同步，数值仿真结果表明了该方法的有效性.

1 超混沌Rossler系统

超混沌Rossler系统的动力学方程［12］：

其中f（x4）＝2b（x4－d）H（x4－d），H（x4－d）是单位阶跃函数，当H（x4－d≥0）＝1，H（x4－d＜0）＝0.系统（1）中：x1，x2，x3，x4，x5为系统的状态变量；a，b，c，d为系统的参数.当参数a＝0.3，b＝4，c＝1，d＝2时，采用四阶Runge－Kutta法得到超混沌Rossler系统的Lyapunov指数谱及吸引子如图1所示.

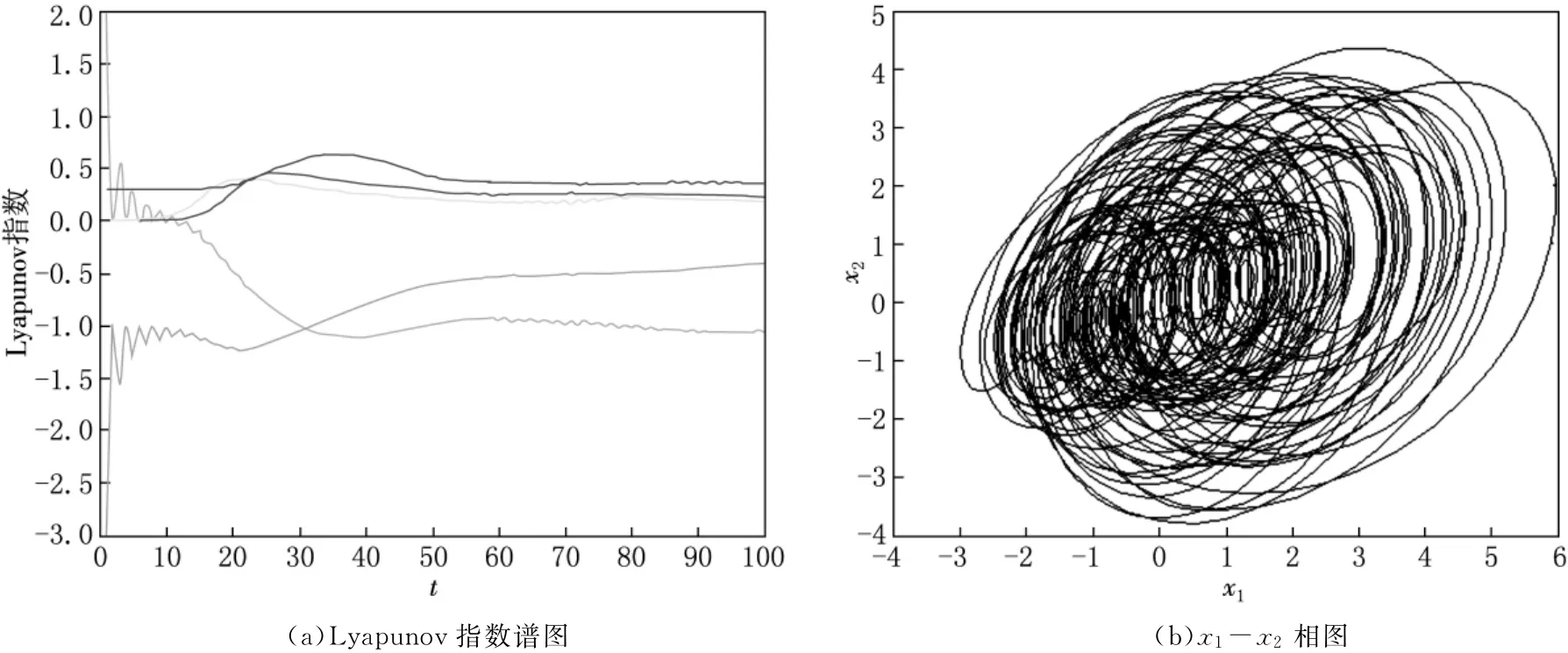
图1 超混沌Rossler系统的Lyapunov指数谱图和吸引子相图

2 超混沌Rossler系统控制器的设计

对超混沌Rossler系统（1）加一个控制器u，则系统方程变为

利用Backstepping方法设计控制器u使系统（2）稳定到一有界点.选取Lyapunov函数

则有

取虚拟函数α1（x1）＝（a＋1）x1.

定义误差变量

得到（x1，¯x2）的子系统为

选择

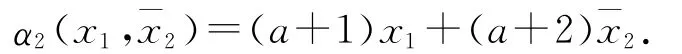
定义误差变量

得到（x1，¯x2，¯x3）的子系统为：

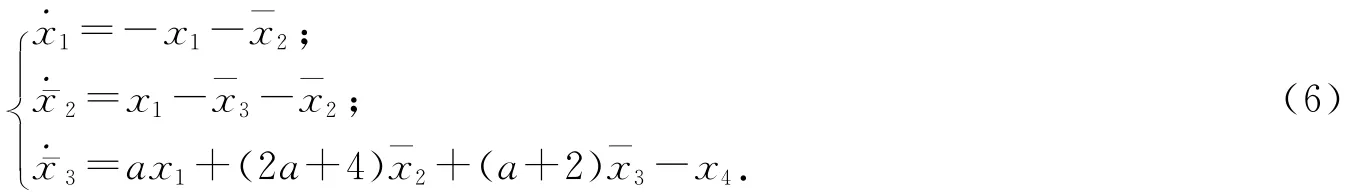
选取

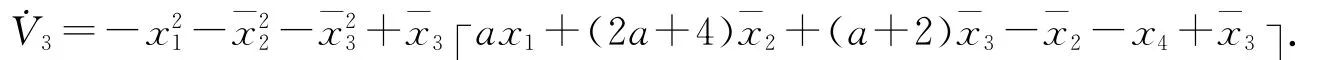
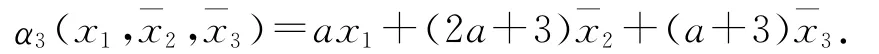
定义误差变量

得到（x1，¯x2，¯x3，¯x4）的子系统为：

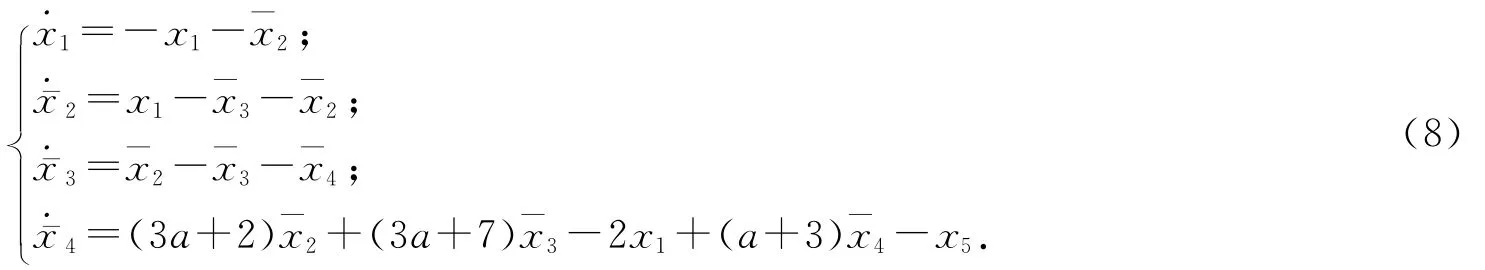
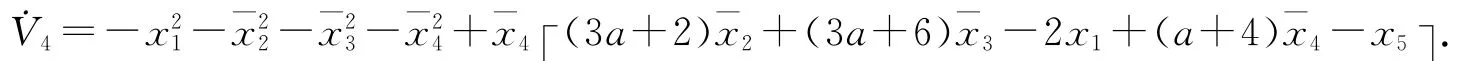
选取

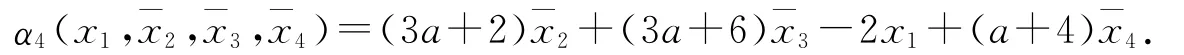
定义误差变量

得到（x1，¯x2，¯x3，¯x4，¯x5）的子系统为：

为使˙V5小于零，选取控制输入

系统（10）在原点（0，0，0，0，0）得到稳定，当t→∞时，（x1，x2，x3，x4，x5）→（0，0，0，0，0）.

取超混沌Rossler系统（2）中的参数a＝0.3，b＝4，c＝1，d＝2，变量的初始值为x1（0）＝1，x2（0）＝1，x3（0）＝－1，x4（0）＝1，x5（0）＝－1，采用的时间步长为0.001，图2为加入控制器u后，超混沌Rossler系统能够被控制到原点（0，0，0，0，0）.

3 超混沌Rossler系统同步

设系统（1）为驱动系统，响应系统为：

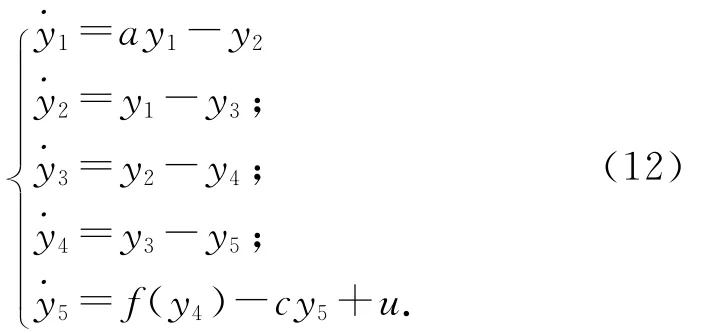
图2 Backstepping方法实现超混沌Rossler系统控制结果

其中f（x4）＝2b（x4－d）H（x4－d），H（x4－d）是单位阶跃函数，同样响应系统中的

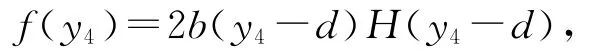
其中u是需要设计的控制器.令误差变量为e1＝y1－x1，e2＝y2－x2，e3＝y3－x3，e4＝y4－x4和e5＝y5－x5，对超混沌Rossler系统（12）控制器的设计如下：

定义z1＝e1＝y1－x1，则˙z1＝ae1－e2，设z2＝e2－α1，其中α1是一个待设计的虚拟控制器.

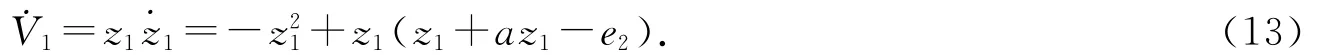
选取虚拟函数α1（z1）＝（a＋1）z1，则˙V1＝－z21－z1z2，˙z1＝－z1－z2.

定义

其中α2是虚拟函数，设z3＝e3－α2，选取Lyapunov函数，则

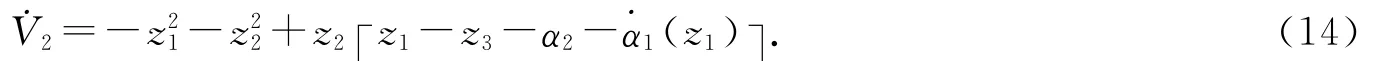
选取虚拟函数α2（z1，z2）＝（a＋1）z1＋（a＋2）z2，则˙V2＝－z21－z22－z3z2，˙z2＝z1－z3－z2.

定义

设z4＝e4－α3，选取Lyapunov函数，则

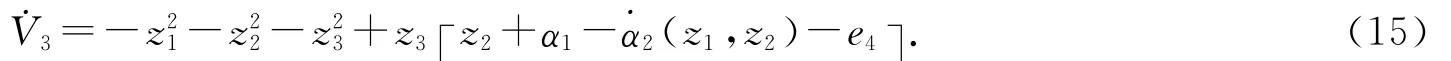
选取虚拟函数α3（z1，z2，z3）＝az1＋（2a＋3）z2＋（a＋3）z3，则

定义

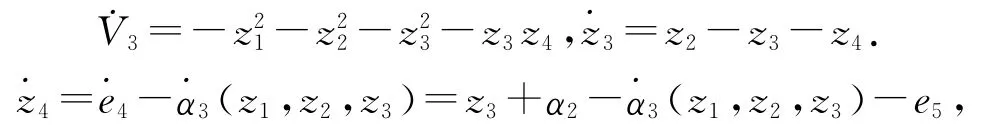
设z5＝e5－α4，选取Lyapunov函数，则

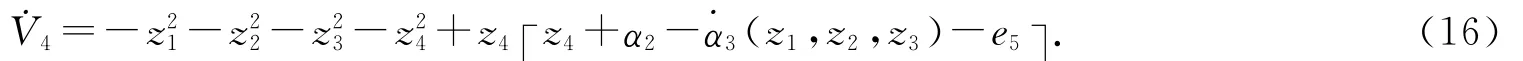
选取α4（z1，z2，z3，z4）＝（3a＋2）z2＋（3a＋6）z3－2z1＋（a＋4）z4，则

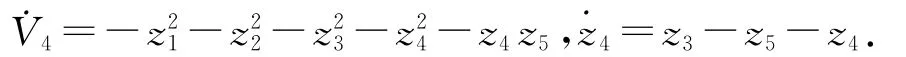
定义

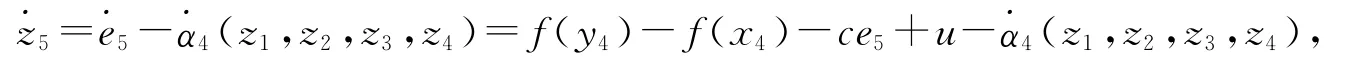
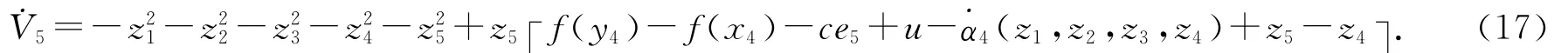
得到控制输入u为

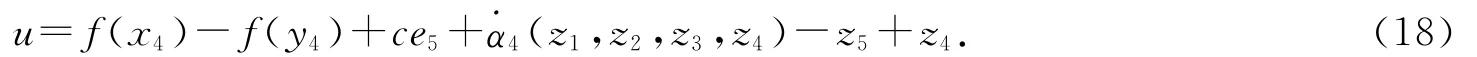
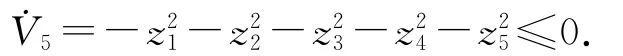
由以上推导可知，当取控制器u时，这就说明在基于Backstepping方法实现超混沌Rossler系统设计的控制器作用下，实现了驱动系统与响应系统的同步.采用四阶Runge－Kutta法求解方程（1）和（12），选取时间步长为0.01s，驱动系统（1）的初始值选取为x1（0）＝1，x2（0）＝2，x3（0）＝3，x4（0）＝4，x5（0）＝5，响应系统（12）的初始值选取为y1（0）＝1，y2（0）＝1，y3（0）＝1，y4（0）＝1，y5（0）＝1，得到同步误差曲线如图3所示.

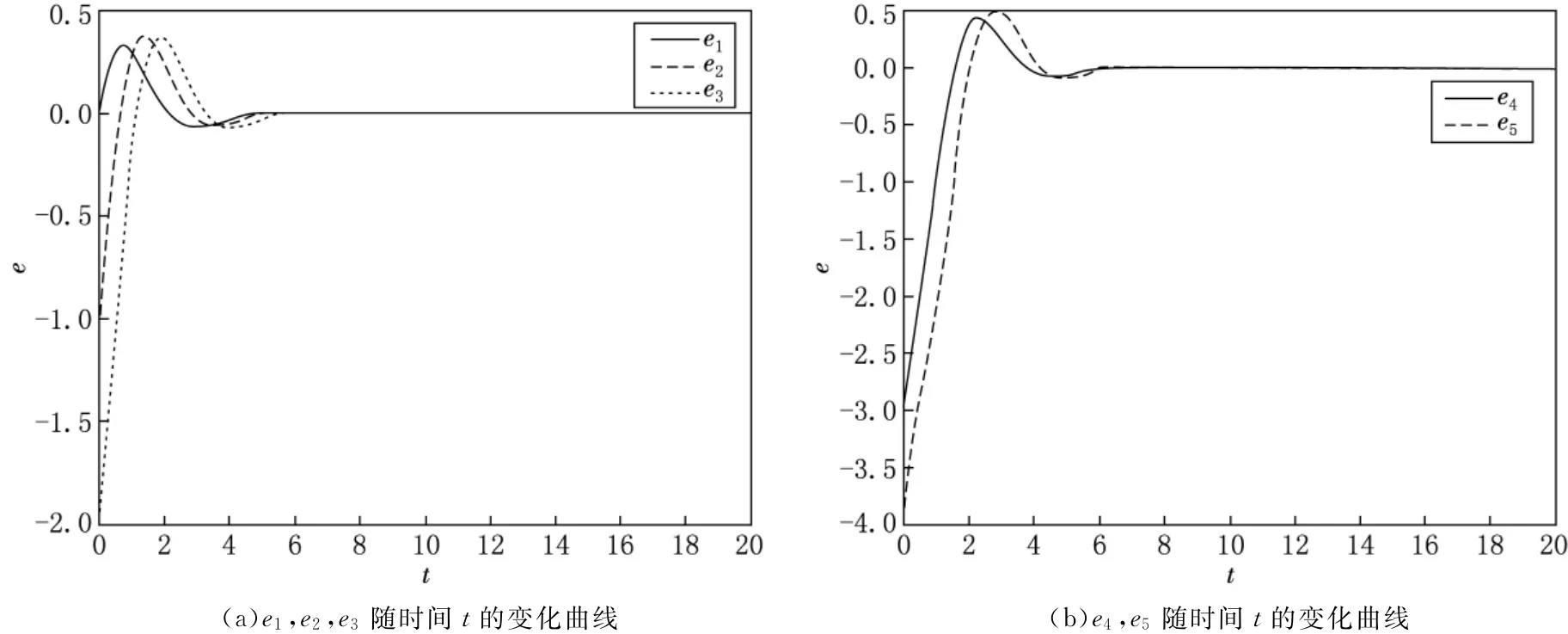
图3 Backstepping方法实现超混沌Rossler系统同步的误差曲线

由图3的数值计算结果可以看出，在很短的时间内，误差e1（t），e2（t），e3（t），e4（t），e5（t）已分别精确地稳定在零点，即驱动系统（1）与响应系统（12）达到了同步.

4 结论

对超混沌Rossler系统，本文利用Backstepping方法，只需要一个控制器实现了超混沌Rossler系统控制到零点，同时也只使用一个控制器，较好地实现了初值不同的2个超混沌Rossler系统同步，数值仿真结果表明了这种控制方法的有效性.

［1］ OTT E，GREBOGI C，YORKE J A.Controlling chaos［J］.Phys Rev Lett，1990，64：1196.

［2］ CHEN G，DONG X.On feedback control of chaotic nonlinear dynamic system［J］.Bifurcation and Chaos，1992，2：407－411.

［3］ CHEN S，LÜJ.Parameters identification and synchronization of chaotic systems based upon adaptive control［J］.Phys Lett A，2002，19（4）：299－353.

［4］ LIAO T L，LIN S H.Adaptive control and synchronization of Lorenz systems［J］.J Franklin Inst，1999，336：925.

［5］ YASSEN M T.Chaos control of Chen chaotic dynamical system［J］.Chaos，Solitons ＆Fractals，2003，15：271.

［6］ WU Z M，XIE J Y，FANG Y Y.Controlling chaos with periodic parametric perturbations in Lorenz system［J］.Chaos，Solitons and Fractals，2007，32：104－112.

［7］ YASSEN M T.Chaos control of Chen chaotic dynamical system［J］.Chaos，Solitons and Fractals，2003，15：271－283.

［8］ YU Y G，ZHANG S C.Controlling uncertain Lüsystem using Backstepping design［J］.Chaos，Solitons and Fractals，2003，15：897－902.

［9］ TAN X H，ZHANG J Y，YANG Y R.Synchronizing chaotic system using Backstepping design［J］.Chaos，Solitons and Fractals，2003，16：37－45.

［10］ YASSEN M T.Controlling，synchronization and tracking chaotic Liu system using active Backstepping design［J］.Phys Lett A，2006，8（67）：1－6.

［11］ YASSEN M T.Chaos control of chaotic dynamical systems using Backstepping design［J］.Chaos，Solitons and Fractals，2006，27：537－548.

［12］ 岳丽娟，陈艳艳，彭建华.用系统变量比例脉冲方法控制超混沌的电路实验研究［J］.物理学报，2001，50（11）：2097－2102.

Controlling and synchronizing hyperchaotic Rossler system using Backstepping design

WANG Shi1，YANG Ji2，LUAN Hong－xia3
（1.Office of Information Management and Planning，Northeast Normal University，Changchun 130024，China；2.Department of Basic Course，Aviation University of Airforce，Changchun 130022，China；3.School of Physics，Northeast Normal University，Changchun 130024，China）

This paper presents a Backstepping design method for controlling and synchronizing hyperchaotic Rossler system.In each recursive procedure，the virtual controller is designed for the differential of Lyapunov function negative definite.The controller is designed when the error system is stabilize by the stability theory of Lyapunov.The only one controller is needed for controlling and synchronizing hyperchaotic Rossler system using Backstepping design.The simulation results verify the effectiveness of involved controllers.

control；synchronize；Backstepping method；hyperchaotic Rossler system

O 415 ［学科代码］ 120·20

A

（责任编辑：石绍庆）

1000－1832（2014）02－0069－05

10.11672／dbsdzk2014－02－014

2014－01－24

国家自然科学基金资助项目（10847110）；吉林省自然科学基金资助项目（201115008）.

王石（1979—），男，硕士，工程师，主要从事信息安全研究.