基于三参数小波变换的地震瞬时属性计算方法及应用

张凤青 ， 宋永忠，高静怀 ，沈加刚

(1.大庆油田工程有限公司，大庆 163712；2.大庆油田有限责任公司 勘探开发研究院，大庆 163712；3. 西安交通大学 电子与信息工程学院波动与信息研究所, 西安 710049)

0 引言

在油气勘探中，地震属性是预测含油气目标的有效手段。目前常用的提取地震瞬时属性方法,是通过对地震信号进行Hilbert变换得到对应的解析信号；然后由解析信号计算瞬时属性(瞬时参数)。由于实际地震资料中存在噪声，而计算Hilbert变换的方法对噪声很敏感，且由于滤波器的截断效应使得计算出的瞬时属性精度低[1]。小波变换是一种时间一尺度域分析技术，利用解析小波把含噪声信号分解到时间—尺度域,信号和噪声在不同的时间—尺度域子空间内得到一定程度的分离[2]，进而在信号子空间计算瞬时参数，噪声得到压制，信噪比得到了改善。因此，利用小波变换能得到含噪信号更好的瞬时属性估计[3]。信号的小波变换不仅取决于信号自身，而且也与所采用的分析小波有关[4-7]。高静怀等[6-8]对地震资料处理及属性提取中分析小波的选择问题进行了系统的研究，认为选择最佳匹配地震子波(BMSW小波)或待分析有效信号的函数作为基本小波有利于压制噪声，并给出了地震子波的模拟公式及相应的分析小波。BMSW小波用于瞬时频率、瞬时带宽等参数提取效果良好，但不能很好地分析含有频率和振幅快速变化分量的信号[8-10]。因此，本次研究针对薄互层地震信号含有快速变化的振幅和频率分量的特点，在最佳匹配地震子波的物理小波基础上提出了新的分析小波即三参数小波，形成了基于三参数小波变换的高分辨率瞬时属性分析方法。

1 方法原理

1.1 三参数小波及其时频特性

文献[8]给出了地震子波的模拟方法及相应的分析小波。从模拟地震子波的公式出发，考虑小波函数的容许条件和归一化条件，可定义新的小波函数

ψ(t;σ,τ,β)=e-τ(t-β)2{p(σ,τ,β)[cos(σt)-k(σ,τ,β)]+iq(σ,τ,β)sin(σt)}

(1)

其中t是时间；σ为分析小波调制频率；τ为能量衰减因子；β为能量延迟因子；p、k、q是待定函数；σ,τ,β∈R且σ,τ≥0(R示实数集合)。

为了书写方便，用向量Λ=(σ,τ,β)记参数σ、τ、β集合，则ψ(t;σ,τ,β)可记为ψ(t;Λ)。相应地，式(1)可简写为

ψ(t;Λ)=e-τ(t-β)2{p(Λ)[cos(σt)-k(Λ)]+iq(Λ)sin(σt)}

(2)

求解p(Λ),q(Λ)和k(Λ)如下：

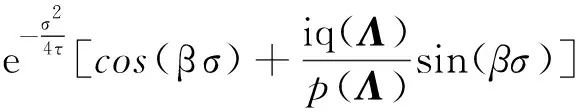
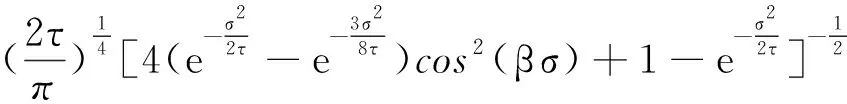
(4)

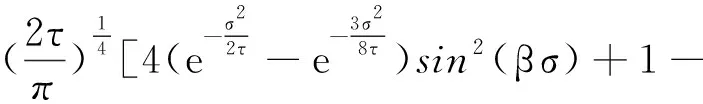
(5)

由式(2)构造的小波函数即为三参数小波。三参数小波有三个可调参数(σ、τ、β)，对信号做小波分析时有很高的自由度,能够很好地匹配地震子波或给定的有效信号；与BMSW小波或其他小波相比，三参数小波有更好的时域局部化性质，适合分析包含频率及振幅都快速变化的分量的信号。

图1是三参数小波与BMSW小波的时-频特性比较，小波参数取Λ=(1,0.5,0)。对于分析包含频率及振幅都快速变化的分量的信号，要想在得到最佳的时间分辨率的同时分离开信号中的各种频率分量，就要求取较小的σ值。当σ较小时(例如σ=1时)，BMSW小波的模在时—频域会出现多个峰(图1(a)、图1(b))。使用具有多峰的分析小波对信号作小波变换会导致信号多个不同位置的局部化，这在瞬时频率及振幅计算中会产生假象[7]，而对相同的参数而言，三参数小波的模仅有一个峰(图1(c)、图1(d))。由此看出，三参数小波在时-频域有比较理想的局部化性质，这使得三参数小波不仅适合分析包含慢变频率和幅度分量的信号，也适合包含快变分量的信号。

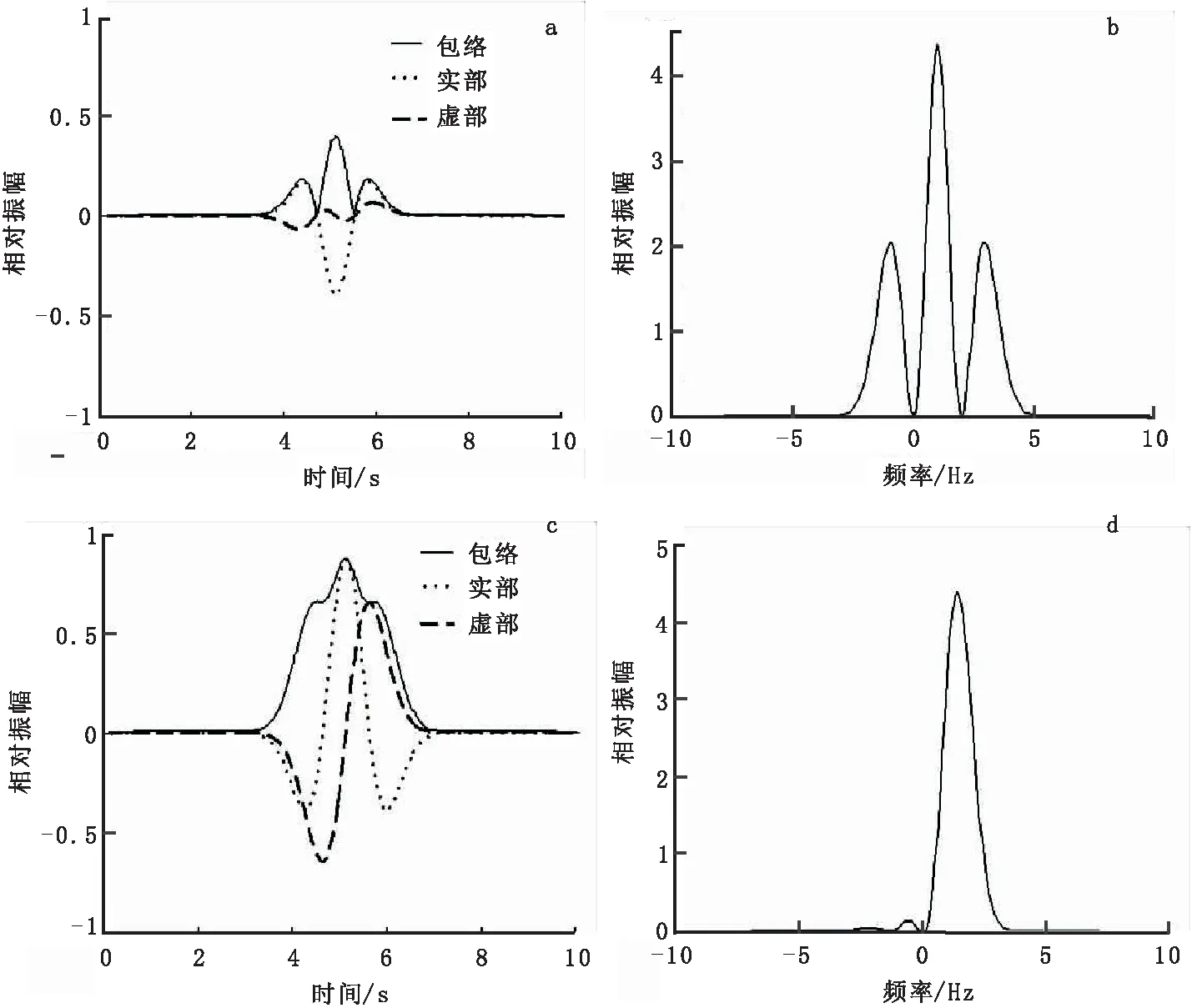
图1 三参数小波与BMSW小波的时-频特性比较Fig．1 The comparison of time-frequency characteristics between three parameters wavelet and BMSW wavelet(a) BMSW小波波形；(b) BMSW小波的Fourier振幅谱；(c) 三参数小波波形；(d) 三参数小波的Fourier振幅谱

图2 三参数小波薄互层模型时-频特性分析Fig．2 Time-frequency characteristics analysis of three parameters wavelet with thin-interbeded model(a)反射系数序列；(b)合成记录；(c)三参数小波时频域能量分布；(d) BMSW小波时频域能量分布

为进一步分析三参数小波的时频特性，设计了如图2所示的薄互层模型。图2(a)为薄互层模型的反射系数序列，其幅度大小相等，正负相间，从200 ms到300 ms，位置分别位于200 ms、 201 ms、 203 ms、… 、 255 ms、 264 ms、 272 ms、…、 300 ms；图2(b)为对应的合成地震记录，其中地震子波采用50 Hz的Ricker子波。

图2(c)为由三参数小波得到的时-频域能量分布图。由于三参数小波有良好的时-频局部化特性，其时-频平面上只有一个主能量带。主能量带的时间中心在0.250 s处(对应最厚层，见图2(a))，沿着主能量带，由中心向两边，随着层的变薄，中心频率(指在给定时刻主能量带中的能量最大值对应的频率)变高，这符合随着层的变薄而调谐频率升高的薄互层时-频响应特性[11]。此外，图2(c)中垂直于时间轴的锥形条纹准确地刻画了薄互层的层状结构，这表明三参数小波具有最佳的时间分辨率。

图2(d)是BMSW小波时-频域能量分布。由于BMSW小波在频率轴上有三个中心(两个在频率正半轴，一个在负半轴，见图1(b))，故在时间-频率域上形成三个能量带(图2(d)中未画出负频率半平面)。这种复杂的时频域能量分布，模糊了薄互层的时-频响应特性，容易导致对地下地质结构的错误解释。

由此看出，拥有三个可选参数的三参数小波，用于像薄互层地震数据这样的信号(含有频率及振幅快速变化的分量)分析是合适的，而BMSW小波(包括Morlet小波)却不能做到这一点。

1.2 三参数小波变换

将三参数小波作为基本小波。对于任意给定的信号s(t)∈L2(R)，L2表示平方可积函数空间，t为时间，s(t)关于分析小波ψ(t)的三参数小波变换为

(6)

式中a、b分别表示尺度及平移参数，a,b∈R且a≠0；ψ*表示取复共轭。由于三参数小波具有理想的时-频能量分布和最佳的联合时-频分辨率特征，因此地震资料的三参数小波变换能够更好地揭示薄互层的时-频响应特性，进而提取瞬时地震属性和刻画薄互层的沉积旋回、研究薄互层内部结构和估算薄层厚度。

1.3 基于三参数小波的瞬时属性计算

文献[1]提出了用小波变换求能量有限实信号对应的解析信号的一个定理,在此基础上给出了用小波变换计算信号瞬时参数的算法。下面列出瞬时频率、瞬时相位及瞬时振幅等参数的计算公式。对于任意给定的信号s(t)∈L2(R)，尺度因子a，可定义瞬时属性如下：

(7)

(8)

(9)

d(t)=abs(e′(t)/2π/e(t)

(10)

其中SR、SI是S(t)对应的复数信号的实部和虚部，e(t,a)、θ(t,a)、ω(t,a)、d(t)依次表示尺度为a时的瞬时振幅、瞬时相位、瞬时频率及瞬时带宽。

2 应用效果

GTZ地区FY油层是目前大庆油田主要勘探目的层，主要储层是河道砂体，砂体厚度薄，一般为2 m～5 m，远远小于地震勘探分辨率，常规方法难以预测，薄层河道砂体地震识别是该区勘探的关键和难题[12]。我们应用三参数小波变换地震瞬时属性方法，对该区薄储层进行了预测，取得了良好效果。

对振幅、频率、相位、带宽4种属性用3个不同参数进行处理，处理参数分别是：

Λ1=(1,0.001,22),f=[3,150]

Λ2=(1,0.001,22),f=[3,200]

Λ3=(1,0.001,22),f=[100,100]

其中Λ1、Λ2是全频段属性，Λ3是100 Hz分频属性。从处理效果看，在频段[3，200 Hz]仍能成像，但效果与[3，150 Hz]差别不大。在分频属性中，分频带宽效果较好。

图3是过G572—G19井三参数小波瞬时带宽与Hilbert变换瞬时带宽剖面对比，可以看出，三参数小波瞬时属性的分辨率明显高于Hilbert变换瞬时属性。

F21x油层组发育1个较厚层砂体，在G572井厚度为6.78 m，在G19井厚度为11.9m，但由于分辨率的限制，在Hilbert变换瞬时带宽剖面上，这个砂体没有明显响应。在三参数小波瞬时带宽剖面上，分辨率明显提高，这个砂体分布得到清晰地刻画，而且还识别出了其他层位上的2 m～3 m的薄砂体。

图4是F21x油层三参数小波瞬时带宽与Hilbert变换瞬时带宽沿层切片，通过对比看出，由于分辨率的提高，三参数小波瞬时带宽沿层切片上，薄层砂体展布范围有所扩大，规律也较明显。用已知井最大单层砂岩厚度进行了验证，Hilbert变换瞬时带宽预测大于2 m砂体符合率只有56%,三参数小波瞬时带宽预测大于2 m砂体符合率达到了73%,薄层砂岩预测能力有较大提高。

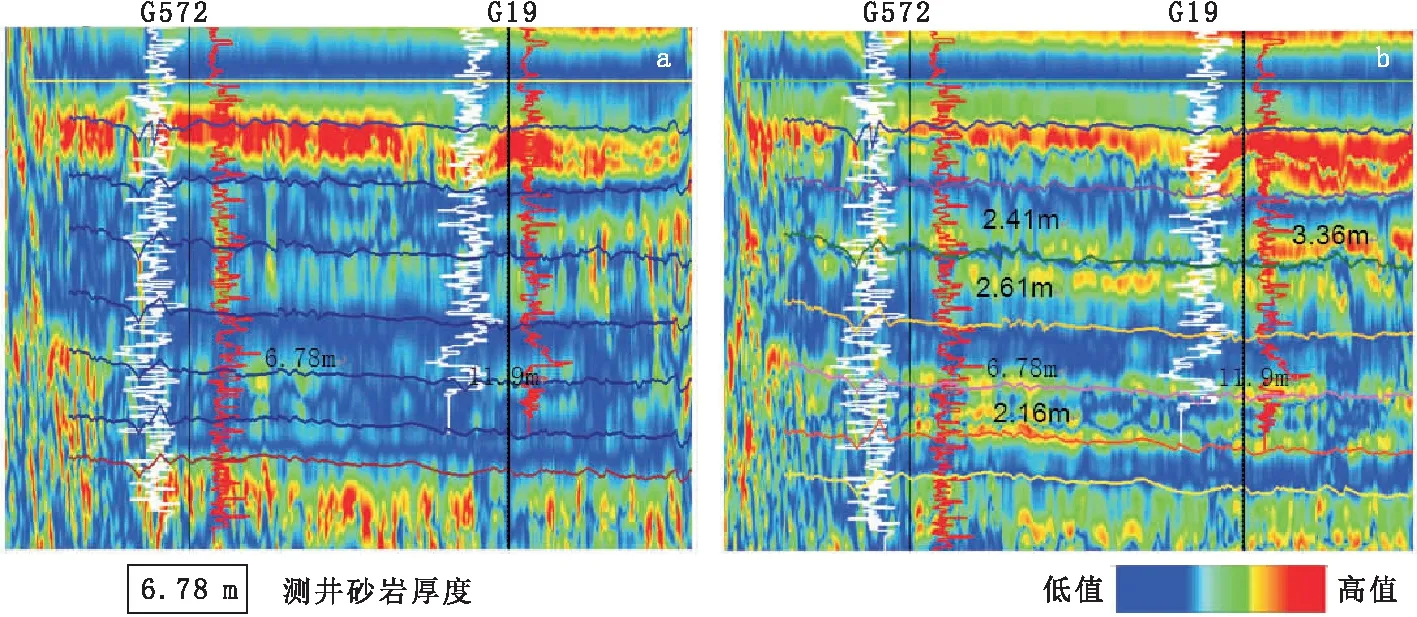
图3 过G572-G19井三参数小波瞬时带宽与Hilbert变换瞬时带宽剖面对比Fig．3 The comparison of instantaneous bandwidth section between three parameters wavelet and Hilbert transform across the G572 - G19 well(a) Hilbert变换瞬时带宽剖面；(b) 三参数小波瞬时带宽剖面

图4 F21x油层三参数小波瞬时带宽与Hilbert变换瞬时带宽沿层切片对比Fig．4 The comparison of instantaneous bandwidth slice between three parameters wavelet and Hilbert transform for the F21x oil layer(a) Hilbert变换瞬时带宽切片；(b) 三参数小波瞬时带宽切片

沉积相研究表明，该区F21x油层河道沉积具有 “北宽南窄，北曲南网，北部点坝发育，南部交叉频繁”的特点[13]，三参数小波瞬时带宽沿层切片揭示的砂体分布特征，符合该区的沉积规律。

3 结论

1) 三参数小波有三个可调参数，对信号做小波分析时有更大的自由度,能够很好地匹配给定的有效信号。

2)与BMSW小波或其他小波相比，三参数小波有更好的时域局部化性质，这使得三参数小波不仅适合分析包含慢变频率和幅度分量的信号，而且也适合包含快变分量的信号。

3)三参数小波变换能够更好地揭示薄互层的时-频响应特性。三参数小波变换瞬时属性比Hilbert变换瞬时属性有更高的信噪比和分辨率，为识别薄层砂体提供了有效手段。

4)基于三参数小波可以进一步开展薄互层的沉积旋回分析、研究薄互层内部结构和估算薄层厚度。

参考文献：

[1] 高静怀，汪文秉，朱光明.小波变换与信号瞬时特征分析[J].地球物理学报，1997,40(6)：821-832.

[2] 周怀来,李枚,郑文锋,等.基于二维小波变换的地震资料去噪方法[J].大庆石油地质与开发，2009,28(4)：121-124.

[3] GAO JINGHUAI, LI YOUMING, CHEN WENCHAO. On the instantaneous attributes analysis of seismic data via wavelet transform[R]. Expanded abstracts of the technical program, SEG 68thannual meeting, 1998:1084-1087.

[4] 李世雄，刘家琦.小波变换和反演数学基础[M]. 北京：地质出版社，1994.

[5] 朱光明，高静怀，王玉贵.小波变换及其在一维滤波中的应用[J].石油物探，1993,32(1)：1-10.

[6] 高静怀，郑庆庆，王大兴，等.基于物理小波的地震资料最佳分辨率解释方法[J].煤田地质与勘探，2004，32(4)：50-53.

[7] 高静怀，满蔚仕，陈树民.广义S变换域有色噪声与信号识别方法[J].地球物理学报，2004,47(5)：867-875.

[8] 高静怀，汪文秉，朱光明，等.地震资料处理中小波函数选取研究[J].地球物理学报，1996,39(3):412-427.

[9] GAO JINGHUAI, WU RUSHAN ,WANG BAOJIANG. A new type of analyzing wavelet best matching seismic wavelets and its applications extraction of the instantaneous spectrum bandwidth[R]. Expanded abstracts of the technical program, SEG 71thannual meeting, 2001:1937-1940.

[10] GAO JINGHUAI, DONG XIAOLONG, WANG WENBING, et al. Instantaneous parameter extraction via wavelet transform[J]. IEEE Tran. On Geoscience and Remote Sensing, 1999,37(2):867-870.

[11] KOEFOED O. , DE VOOGD N. DE . The linear properties of thin layers, with an application to synthetic seimograms over coal seams[J].Geophysics,1980,45(8):1254-1268.

[12] 张尔华，宋永忠，李昂，等.扶杨油层河道砂体地震识别技术[J].大庆石油地质与开发，2009,28(5)：288-294.

[13] 陈树民，沈加刚，宋永忠，等.基于沉积模式的地震多属性量化沉积微相解释方法——以松辽盆地北部高台子地区泉头组三-四段为例[J].地质科学，2009,44(2)：740-757.