超大型风机安装平台自升状态下的运动响应频域分析
2014-06-27,,,
, , ,
(1.南通中远船务工程有限公司,江苏 南通 226006;2:江苏科技大学 船舶与海洋工程学院,江苏 镇江 212003)
自航自升式风机安装船兼有运输平台和作业平台的作用,具有运载航行、船体平台升降、起重作业等综合功能,船型扁平,带有数根桩腿,装备有超高起吊高度的重型起重机[1]。第三代超大型自航自升式风机安装平台抗风浪能力强,可装运10台大功率风力发电机,工作效率高,已成为海上风机安装的主流装备。
针对风机安装作业平台的外部环境,以及船型特征,应用基于三维线性势流理论的水动力分析计算软件SESAM,分析船体平台在风电场作业前就位过程中的运动响应,以期得到这种船型的运动响应规律,用于指导船型设计及施工。
1 自升式风机安装作业平台载荷与运动响应计算方法
在线性化假设的基础上,再加上细长体假定,就可以运用切片法和谱分析法在预报船舶在波浪上的运动性能[2]。St.Denis和Pierson理论表明[3],浮体在不规则海浪中运动响应可以由单位规则波中的响应(传递函数)和海浪谱来确定。风机吊装平台的运动响应可通过计算传递函数和不规则波统计预报的谱分析法进行。
1.1 规则波中船体运动与载荷计算
在规则波中船体运动与载荷计算广泛应用三维源汇理论,其基本假定为[3]
1)船体运动及波浪均是微幅线性的;
2)视水为无粘性流体;
3)考虑绕射和辐射的影响。
建立包括船体及桩腿在内的平台整体的频域运动方程[5]
[-ω2(M+A(ω))+iw(B(ω)p+Bv)+
C]x(ω,β)=F(w,β)
(1)
式中:ω——入射波角频率;
β——入射波传播方向;
M——浮体惯性矩阵;
A(ω)——与频率有关的附加质量矩阵;
B(ω)p——与频率有关的辐射阻尼矩阵;
Bv——与流体粘性有关的线性阻尼矩阵;
C——静水回复刚度矩阵;
x(ω,β)——浮体运动矩阵;
F(ω,β)——波浪激励力矩阵,由作用在大尺度构件上的波浪激励力和作用在小尺度构件上的惯性力,以及拖曳力组成。
1.2 波浪载荷
采用绕射理论,通过对作用在船体湿表面上整个水动压力的积分计算波浪载荷。流场用速度势函数来描述,总速度势由入射势、绕射势和船体平台在静水中产生的辐射势组成。速度势应在流体各处满足拉普拉斯方程,及物体表面、自由表面、海底及无穷远处的边界条件。
桩腿符合小尺度构建D/L≤0.2(D为截面的特征尺度;L为入射波波长)的判别条件,其单位长度dz上的波浪载荷dF采用Morison公式计算。

(2)
式中:dF1——桩腿单位长度上的惯性力;
dFD——桩腿单位长度上的拖曳力;
ρ——海水密度,1 025 kg/m3;
CM——惯性力系数,对于圆柱构件,
C=1.3~2.0;
CA——附加质量系数,CA=CM-1;
CD——拖曳力系数,对于圆柱构件,
CD=0.6~1.2;
u——垂直于桩腿轴线的水质点速度分量;



采用波谱计算,需要按等效线性化方法对速度平方项进行处理[6]。
(3)

其中:Su(ω)——水质点速度的频率谱,可以根据波谱计算得到[7]。
1.3 传递函数与响应谱
传递函数[8](RAO)是浮体在单位波幅的简谐波作用下的浮体响应。在简谐波作用下随时间而变化的响应函数可写为
R(ω,β,t)=A·Re[|H(ω,β)|·ei(ωt+φ)]
(4)
式中:H(ω,β)——传递函数。
计算出传递函数H(ω)后,根据给定的波谱Sη(ω),即可求得结构的响应谱。
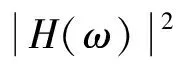
(5)
运动响应分析计算应用SESAM软件中基于绕射理论和Morison理论计算波浪载荷Wadam(wave analysis by diffraction and morison theory)模块进行,可用于分析任意固定或者零航速浮式结构物与波浪的相互作用,适用于有限和无限水深。
1.4 波浪谱
波浪谱密度函数Sη(ω)是平稳随机过程的频率描述。不规则波谱表示了不规则波内各个单元谐波的能量分布情况。不同波谱模型对波浪载荷存在一定的影响,对于沿海区域,通常采用JONSWAP谱。JONSWAP谱是有中等风况和有限风距情况测得的,其主要特点是考虑了有限风压的作用。多数使用经验表明,此谱和实测结果是符合的,适用于不同成长阶段的风浪[9]。风电场主要分布在沿海区域,故采用JONSWAP谱。
(6)
式中:α——能量尺度参量;
β——形状参数,一般取1.25;
σ——谱宽参数,ω≤ωp时,σa=0.07,ω>ωp时,σb=0.09;
γ——谱峰值参数。
2 环境载荷与计算模型
所研究对象为超大型海上风机安装作业平台,是一种集自航运输、自升平台、起重船等多种功能为一体的新型船舶。其主要参数见表1。

表1 平台主尺度及主要参数
2.1 平台载荷的确定
安装作业平台的排水量为23 675 t,空载重量为14 992 t。甲板载荷为5 000 t,燃油重量约为850 t,滑油及液压油重量约为16.2 t,淡水重量约为450 t。安装作业平台甲板载荷为5 000 t,其中包括10台风机。选取西门子3.6 MW风机为例,计算风电机组的重量。叶轮为120 m,叶轮叶片为58.5 m,塔架高度为90 m或者按现场来定。叶轮重100 t,机舱125 t,按照总布置图分配在甲板上。将海洋环境系数施加在模型上,具体为在其就位工况自升时,考虑最大波高为1.8 m,波浪周期为8 s,风速为14 m/s。
2.2 计算模型
运用SESAM程序中的GeniE模块建立自升式风机安装作业平台的水动力三维模型,包括湿表面模型、Morison模型。计算时采用的坐标系x方向指向船首,y方向指向左舷,z方向向上,坐标原点在基线面,0站号。建立整体结构模型见图1。

图1 海上风机安装作业平台整体模型示意
将平台表面船体部分定义为湿表面,对湿表面(T1.FEM)进行网格划分,建立湿表面模型见图2。将桩腿部分建立成Morison(T2.FEM)模型见图3。根据平台的空船重量,以及可变载荷数据建立质量模型(T3.FEM)见图4。

图2 湿表面模型

图3 Morison模型

图4 质量模型
3 平台就位过程工况的运动响应频域计算分析
3.1 规则波下平台运动响应
以桩腿下放22.5 m为例,计算平台自升就位时运动响应。平台左右对称,浪向角取值范围为0°~180°,间隔为15°。波浪周期取值范围为5~55 s,间隔为2 s。采用JONSWAP谱模拟短期海况,谱峰因子取2,有义波高1.8 m,周期为8 s。应用SESAM后处理模块Postresp,对计算结果进行后处理。见图5。
由图5可见,平台的垂荡运动在波浪周期为8~12 s时比较剧烈,变化比较大,最大值出现在浪向角为45°,周期为10 s时。最小值出现在浪向角为90°,波浪周期为9 s时。垂荡运动严重影响桩腿与海底的接触,尤其是当桩腿快接近海底时垂荡运动要引起足够的重视。过大的垂荡运动会给平台就位过程带来不便,因此就位时应该避开波浪周期为9 s左右的波能范围,并且避开180°的浪向,比较有利于安装作业。
平台的纵摇运动在波浪周期为8~12 s区域内运动比较剧烈,在浪向角为45°时运动幅度最大,在周期为9 s区域达到极值0.027 (°)/m,在浪向角为90°时运动幅度最小,在周期为9 s区域内极值为0.002 48 (°)/m。
平台的横摇运动总体幅值较小,但在波浪周期为15 s时幅值迅速变大,达到极值时迅速变小。在浪向角为90°时横摇运动在15 s区域内达到极值0.244 (°)/m。平台横摇运动与15 s周期的波浪容易发生共振,横摇较大会引起作业的不便和工作人员晕船等不适合插桩就位的现象,因此在就位尤其是桩腿接近海底插桩时应当尽量避免在波浪周期为15 s区域内作业。
平台的纵荡、横荡和艏摇运动没有回复力回复力矩,运动幅值会随着波浪周期的增大而增大。纵荡运动在浪向角为180°时运动最大。横荡运动在波浪周期为15 s时会出现一个极值,浪向角为90°时极值最大为3.09,波浪周期为15 s之后运动会逐步变小,17 s之后运动幅值又会随着波浪周期的增大而增大。艏摇运动在波浪周期为15 s处也会出现极值,浪向角为135°时极值最大为0.016 (°)/m,在15 s之后的运动幅值变小,随着波浪周期的变大幅值变化将不会发生太大变化。
3.2 运动响应的谱分析
以下放22.5 m为例,根据自升就位时环境要求,给定海况T=8 s,Hs=1.8 m,浪向角为0°,选取了JONSWAP谱,计算得到安装作业平台的响应谱见图6。
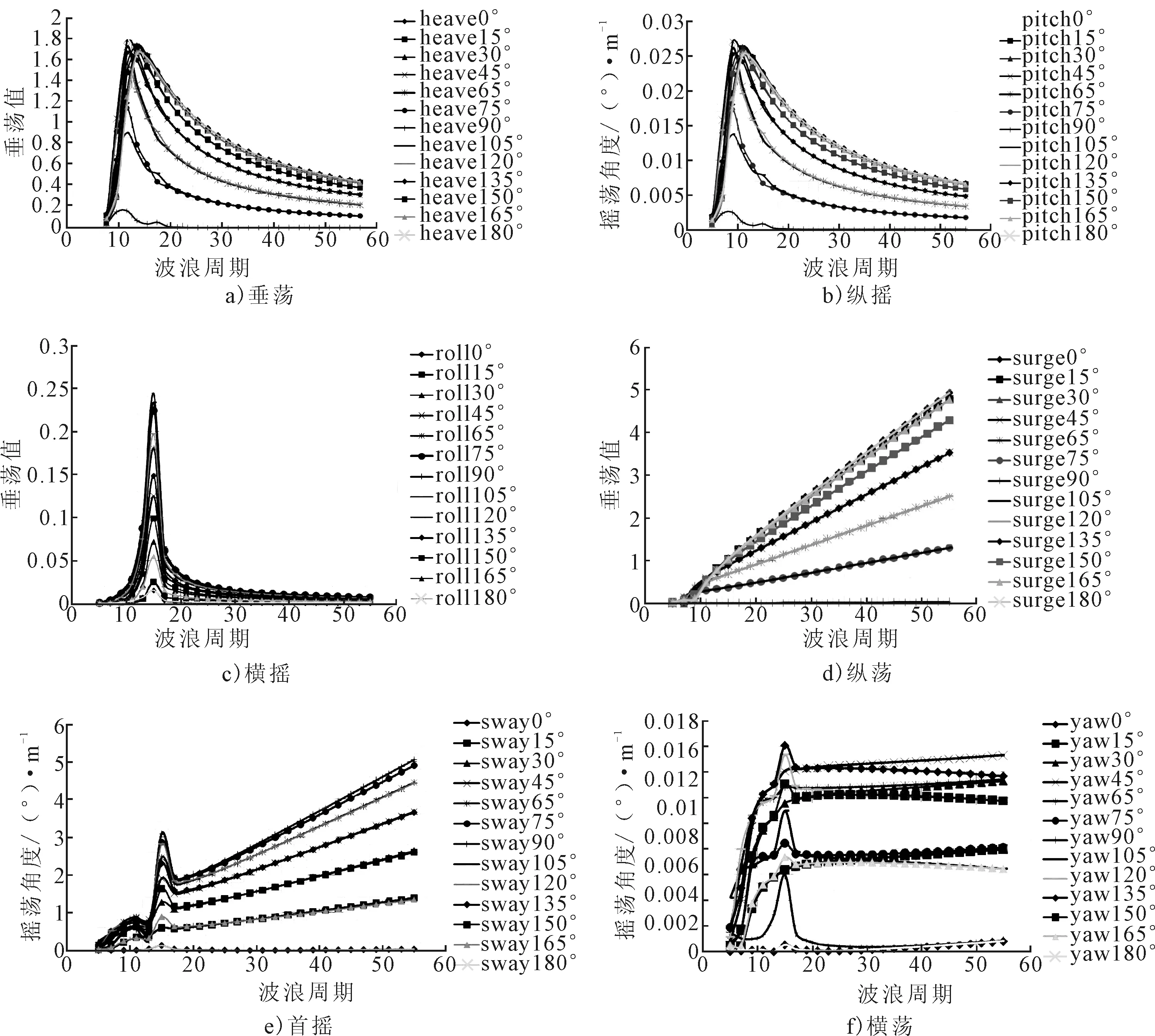
图5 运动传递函数

图6 响应谱
由图6可得,安装作业平台垂荡、纵摇运动周期为10 s的波频运动为主要成分,横摇运动周期为14 s的波频运动为主要成分,纵荡、横荡、艏摇运动周期为11 s左右波频运动主要成分,这些结果与系统的固有周期相关。文中所研究的平台服务于欧洲海域,根据北大西洋波浪散布图,5.5~10.5 s较为典型,并且此平台设计说明书要求就位工况海洋环境波浪周期为8 s,避开了平台固有周期。
4 结论
1)浪向角以及波浪周期对平台影响很大。
2)垂荡在浪向角为45°,波浪周期为10 s时最大,幅值最大为1.672。垂荡运动严重影响桩腿与海底的接触,尤其是当桩腿快接近海底时垂荡运动要引起足够的重视。过大的垂荡运动会给平台就位过程带来不便,因此就位时应该避开波浪周期为10 s左右的波能范围,并且避开45°和180°的浪向,比较有利于安装作业。
3)横摇在浪向角为90°,波浪周期为15 s时最大。平台横摇运动与15 s周期的波浪容易发生共振,横摇较大会引起作业的不便和工作人员晕船等不适合插桩就位的现象,因此在就位尤其是桩腿接近海底插桩时应当尽量避免在波浪周期为15 s区域内作业。
4)平台的纵荡、横荡和艏摇运动没有回复力回复力矩,运动幅值会随着波浪周期的增大而增大。
[1] 姚震球,唐文献,马 宝,等.海上风电安装船关键部位结构强度研究[J].中国造船,2012,53(2):79-87.
[2] 贺五洲,周正全.水深对船舶运动和波浪载荷的影响[J].中国造船,1997(2):1-7.
[3] 张海彬,程维杰.U型半潜式起重铺管平台水动力分析[J].海洋工程,2010,28(4):40-45.
[4] 冯铁城,朱文蔚,顾树华.船舶操纵与摇荡[M],北京:国防工业出版社[M].1989.
[5] 何 堃,唐友刚,邵卫东,等.自升式钻井平台就位过程桩腿触底分析[J].中国海洋平台,2012,27(2):41-46.
[6] 阮胜福,海上风电浮式基础动力响应研究[D],天津:天津大学,2010.
[7] RIAAN van’t Veer. Application of linearized Morison load in pipe lay stinger design[C]∥Proceedings of the ASME 27th International Conference on offshore Mechanics and Arctic Engineering. Estoril,ASME,2008:OMAE 2008-57247.
[8] C.Gudes Soares. On the uncertainty in long-term prediction of wave induced loads on ships[J].Marine Structure, 1999,12(3):171-182
[9] 俞聿修,柳淑学.随机波浪及其工程应用[M].大连:大连理工大学出版社,2011.
